Taller sobre integrales

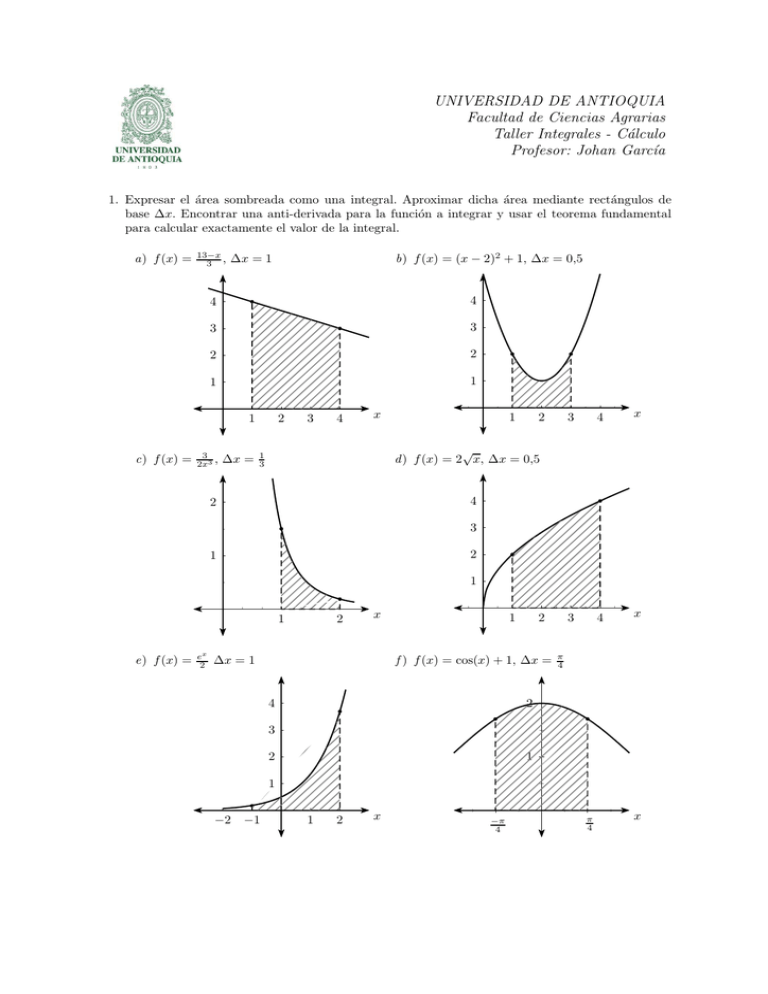
UNIVERSIDAD DE ANTIOQUIA
Facultad de Ciencias Agrarias
Taller Integrales - Cálculo
Profesor: Johan Garcı́a
1. Expresar el área sombreada como una integral. Aproximar dicha área mediante rectángulos de
base ∆x. Encontrar una anti-derivada para la función a integrar y usar el teorema fundamental
para calcular exactamente el valor de la integral.
a) f (x) =
13−x
3 ,
4
4
3
3
2
2
1
1
1
c) f (x) =
b) f (x) = (x − 2)2 + 1, ∆x = 0,5
∆x = 1
3
2x3 ,
∆x =
2
3
4
x
1
2
3
4
x
3
4
x
√
d ) f (x) = 2 x, ∆x = 0,5
1
3
4
2
3
2
1
1
1
e) f (x) =
ex
2
2
x
∆x = 1
1
2
f ) f (x) = cos(x) + 1, ∆x =
4
π
4
2
3
2
1
1
−2 −1
1
2
x
−π
4
π
4
x
g) f (x) = 2 − x1 , ∆x = 0,5
h) f (x) = 2 sen x, g(x) = 2 cos x, ∆x =
2
2
1
1
π
4
b
1
2
3
4
x
−1
−1
−2
−2
El área entre dos curvas f > g se expresa cómo
de x para los cuales f (x) = g(x).
Rb
f (x) − g(x) dx donde a < b son los valores
j ) f (x) = 45 x + 32 , g(x) =
i) f (x) = 1, g(x) = −x2 + 2, ∆x = 0,5
2
4
1
3
−2 −1
−1
1
2
∆x = 0,5
1
1
−1
4
4
3
3
2
2
1
2
3
x
b
1
b
1
2
√
l ) f (x) = 2 x, g(x) = 41 x2 ∆x = 1
k ) f (x) = 5 − x2 ,g(x) = 41 x2 ∆x = 1
−2 −1
4
(x−3)2 ,
2
x
−2
b
a
x
π
2
−π
2
x
1
2
3
4
x
2. Evalué cada una de las siguientes integrales y dibuje la región correspondiente. Realice las sustituciones indicadas (no olvide escribir dx en términos de du).
a)
b)
Z
0
2
2 − x dx
Z
0
1
e2x dx
u = 2x
c)
g)
1
Z
Z
2
−1
1 − x dx
2
0
1 − (x − 1)2 dx
u=x−1
h)
d)
Z
2
x
0
−e dx
Z
0
1
x
dx
1−x
e−x dx
−2
u = −x
i)
e)
Z
−1
−2
Z
1
+ 1 dx
x
−1
u=1−x
j)
f)
Z
1
5
Z
√
x − 1 dx
5
3
√
2x − 5 − 1 dx
u = 2x − 5
3. Calcule las integrales indeterminadas, es decir, encuentre la anti-derivada.
f)
a)
Z
2
Z
4
2 + 4x − 3x + x dx
p
x x2 + 1 dx
g)
b)
Z
Z
(x + 1)(x − 1) dx
3x dx
(Recuerde: 3x = ex ln 3 )
c)
Z
h)
(x − 1)4 dx
Z
d)
Z
x
dx
2 − x2
i)
Z
sen(2x) dx
e)
x2
√
dx
x3 + 2
j)
Z
Z
3
sen x cos(x) dx
ln x
dx
x
Las siguientes integrales pueden resolverse usando el método de integración por partes.
k)
Z
x cos(2x) dx
u=x
dv = cos(2x) dx
l)
Z
(2x + 1)e−x dx
u = 2x + 1
dv = e−x dx
m)
Z
x ln x dx
u = ln x
n)
Z
ln x dx
dv = x dx