ADST200806-E.pdf
Anuncio

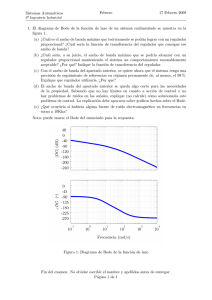
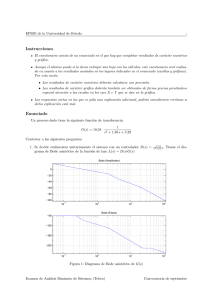
Examen de Análisis Dinámico de Sistemas (2o Teleco) curso 2007/2008 Problema 1 (4 puntos) Dado un sistema de entrada u(t) y salida y(t), especificado por la siguiente ecuación diferencial ÿ(t) + u(t)ẏ(t) + 5y(t) = 3u̇(t) + 10u(t) se pide: 1. Linealizar en torno al punto de equilibrio donde la salida vale y0 = 12. 2. Calcular la respuesta del sistema mediante aproximación lineal cuando la entrada u(t) aumenta dos unidades desde el valor de equilibrio especificado en el apartado anterior. 3. ¿A qué valor tiende la salida y(t) cuando t tiende a infinito? Problema 2 (4 puntos) Dada la función de transferencia de un sistema que se quiere controlar G(s) G(s) = s+5 s(s + 10)(s2 + 3s + 4) (1) con realimentación negativa y unitaria, con un regulador proporcional de constante Kp > 0, se pide: 1. Dibujar el diagrama de Bode del sistema G(s). 2. Aplicando el criterio de estabilidad de Nyquist, ¿existe algún valor de Kp lı́mite que hace que el sistema realimentado pase de estable a inestable o viceversa?¿Cuál? 3. Hallar los márgenes de ganancia y de fase del sistema realimentado y señalarlos gráficamente en el Bode. Cuestión (2 puntos) Dada la función de transferencia Ga (s) = T1 s + 1 (T2 s + 1)(T3 s + 1) y la función de transferencia Gb (s) = T1 s + 1 (T2 s + 1)(T3 s + 1)(Tp s + 1) tales que T1 , T2 , T3 > 0 y Tp > 0, explicar qué diferencias en amplitud y fase habrá entre sus respectivas respuestas ante una señal u(t) = A sen(ωt) EPSIG - Universidad de Oviedo 11 de junio de 2008