ejersisgau42

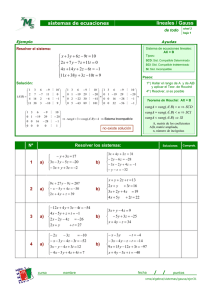
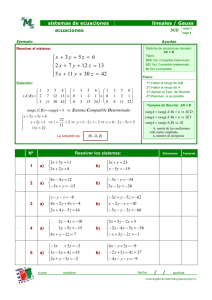
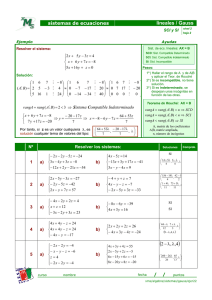
sistemas de ecuaciones
lineales / Gauss
con parámetros
Ejemplo
nivel 4
hoja 2
Ayudas
Discutir según los valores de k y resolver el sistema:
Se puede resolver, también por la
2 x + ky = 0

 x + kz = k
 x + y + 3z = 5

Regla de Cramer,
a veces de modo más simple
1
3
M
5  1 1
3
M
5 
1 1 3 M 5 1

 
 

Solución: ( AM B) =  1 0 k M k  ≈  0 − 1 k − 3 M k − 5  ≈  0 − 1
k −3 M k −5 
 2 k 0 M 0   0 k − 2 − 6 M − 10   0 0 k (k − 5) M k (k − 7) 

 
 

* Si k = 5 : rangA = 2 ≠ rang ( AM B) = 3 ⇒ SI : No hay solución
* Si k = 0 : rangA = 2 = rang ( AM B)
⇒ SCI :
 x + y + 3z = 5
⇒ y = 5 − 3 z ⇒ x = 0 , Soluciones:

 y + 3z = 5
* Si k ≠
(0, 5 − 3λ , λ )
5
: rangA = rang ( A M B ) = 3 ⇒ SCD :
0
 x + y + 3z = 5
k ( k − 7) k − 7
−4
2k

=
⇒y=
⇒x=
 y + (3 − k ) z = 5 − k ⇒ z =
k ( k − 5) k − 5
k −5
k −5
k (k − 5) z = k ( k − 7)

Nº
1
2
3
5
 1
1
1 


,
,
 ( k − 3) (k − 3) (k − 3) 
Resolver los sistemas:
a)
 x + 2 y + z + 2t = 18
 2 x + 2 y + 3z − 3t = 15


− 3 x − 3 y + 2 z + 2t = −3
 6 x − y − 8 z − t = a + 1
a)
(1 − a ) x + ( 2a + 1) y + (2 a + 2) z = a

ax + ay = 2a + 2
2 x + ( a + 1) y + (a − 1) z = a 2 − 2a + a

a)
2(a + 1) x + 3 y + az ) = a + 4

(4a − 1) x + ( a + 1) y + (2 a − 1) z = 2a + 2
(5a − 4) x + (a + 1) y + (3a − 4) z = a − 1

a)
 x cos a + y sen a = 1

 x sen a − y cos a = 1
curso
nombre
b)
b)
Soluciones
Comprob.
2 x − y + 3 z − 1 = 0

x + 2 y − z + b = 0
 x + ay − 6 z + 10 = 0

b)
x + y + z = a

x + y + z = b
x + y + z = c

b)
x − 2 y + z = 0
− x + y + bz = 1


2 x − 2 y + z = 1
ax − 2 y + z = −3
2 x − y + z = 3

x − y + z = 2
3 x − y − az = b

fecha
/
/
puntos
xms/algebra/sistemas/gauss/ejer42