Antena de onda progresiva

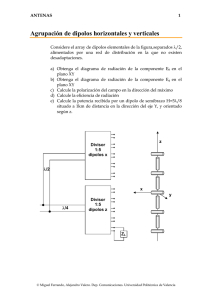
ANTENAS
1
Antena de onda progresiva
Una antena de onda progresiva está formada por un hilo de longitud
L=3λ, separado una distancia h=0.25λ del suelo conductor perfecto,
La línea de transmisión está terminada en una carga Z0, del mismo
valor que la impedancia característica de la línea.
L
Z0
h
Para dicha antena, obtener
a)
b)
c)
d)
La distribución de corrientes
El vector de radiación, incluyendo el plano de masa
Los campos radiados
La posición del máximo y de los ceros del diagrama de radiación
Solución
Corrientes
Las corrientes son las de la línea de
transmisión. Aplicando la teoría de imágenes,
las corrientes equivalentes tienen signo
contrario.
La expresión de I es
I ( z ') = Ie
y
I
2h
x
-I
− jkz '
La corriente imagen es
I ( z ') = − Ie − jkz '
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
2
Vector de radiación
El vector de radiación de un hilo largo de corrientes es
G
N = zˆ ∫
L
2
L
−
2
⎛ (k − k ) L ⎞
sin ⎜ z
⎟
2
sin ( u )
⎝
⎠ = zIL
− jkz ' jk z z '
ˆ
ˆ
Ie e dz ' =zIL
u
⎛ ( kz − k ) L ⎞
⎜
⎟
2
⎝
⎠
Teniendo en cuenta el efecto de la imagen
G G
jk h
−k h
N = N0 e y − e y
(
)
Campos radiados
El campo eléctrico radiado por un hilo aislado es
Eθ = − jω Aθ = jω Az sin θ = jω
µ e− jkr sin u
IL
sin θ
4π r
u
L⎞
⎛
u = ⎜ ( kz − k ) ⎟
2⎠
⎝
Teniendo en cuenta el efecto de la imagen
µ e− jkr sin u
jk h
−k h
Eθ = − jω Aθ = jω Az sin θ = jω
IL
sin θ e − e
4π r
u
k x = k sin θ cos φ
k y = k sin θ sin φ
(
y
y
)
k z = k cos θ
En la siguiente página se muestran los diagramas de radiación en el
plano ZY, así como los diagramas tridimensionales correspondientes
al hilo aislado, la interferencia y el diagrama total.
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
3
90
120
0.542
60
0.4
150
30
0.2
Total ( θ )
180
0
0
210
0
330
240
300
270
θ
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
4
Ceros del diagrama
Los ceros aparecerán para los valores que cumplan la condición
µ e − jkr sin u
jk h
−k h
=0
Eθ = jω
IL
sin θ e − e
4π r
u
u = −π , −2π , −3π ,...
(
y
y
)
L⎞
⎛
u = ⎜ ( k cos θ − k ) ⎟
2⎠
⎝
Los valores de los ceros son
48.2o,70.5o,90o,109.5o,131.8o,180o
Máximo del diagrama de radiación
El máximo se puede calcular de forma aproximada
L⎞
π
⎛
um = ⎜ ( k cos θ m − k ) ⎟ ≈ −
2⎠
2
⎝
θ m =33.5o
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia