Schelkunoff

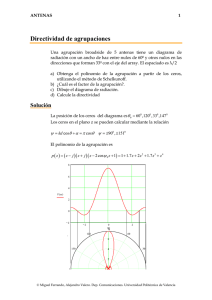
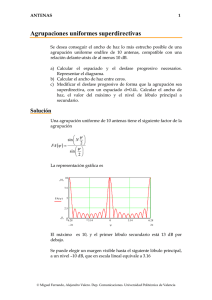
ANTENAS
1
Diseño de Schelkunoff
Se desea diseñar un array distribuyendo los ceros de p(z) en el plano
z. Las condiciones que debe cumplir son las siguientes
•
•
•
•
•
Array broadside
Separación entre elementos d=5λ/8
Ancho de haz entre nulos ∆φ=31º
6 lóbulos secundarios en el margen visible
Nulo de radiación en el eje de la agrupación
Se pide
a) Obtener la distribución de ceros de forma que los coeficientes del
polinomio p(z) sean reales.
b) Obtener la distribución de corrientes
c) Obtener la relación NLPS entre el lóbulo principal y todos los
secundarios
d) Dibujar un corte del diagrama de radiación en el plano de la
agrupación
e) Se dispone de divisores de potencia simétricos de una entrada y
dos salidas. Diseñar una red de distribución adecuada para la
agrupación.
Solución
De acuerdo con las especificaciones dadas, el margen visible
correspondiente a la agrupación broadside es
⎡ 5π 5π ⎤
ψ ∈ [ −kd, kd ] = ⎢ − , ⎥
⎣ 4 4 ⎦
Como el espaciado es superior a λ/2, el margen visible es superior a
una vuelta sobre el círculo unidad en el plano complejo z.
Los extremos del margen visible deben coincidir con un nulo en el
diagrama de radiación, (eje de la agrupación). El eje corresponde a
los ángulos θ=0, y θ=π. La posición del primer nulo se calcula a partir
de la especificación del ancho de haz.
Los nulos en el diagrama de radiación estarán en
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
2
ψ0 =
5π
⎛ π ∆θ
cos ⎜ ± ceros
4
2
⎝2
90
120
π
⎞
⎟=±
3
⎠
Eje imaginario
60
0.8
0.6
150
30
0.4
Eje real
0.2
180
0
0
210
330
240
300
270
3.414
4
3
FA( ψ )
2
1
0.018
0
5
0
− 2π
5
ψ
2π
Margen visible
El diseño especificado tiene cuatro lóbulos secundarios en el margen
visible. Si se añade un nuevo cero ( ) en z=-1
90
120
Eje imaginario
60
0.8
0.6
150
30
0.4
Eje real
0.2
180
0
0
210
330
240
300
270
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
3
El nuevo factor de array es
6.828
8
6
FA( ψ )
4
2
0
0
5
0
− 2π
5
ψ
2π
Margen visible
Con la anterior configuración se tendrían 6 lóbulos secundarios en el
margen visible. También sería correcto añadir dos ceros complejos
conjugados, de forma los coeficientes de la agrupación fuesen reales
Polinomio de array y corrientes
El polinomio del array se puede calcular a partir de sus ceros
π
π
5π
5π
j ⎞⎛
− j ⎞⎛
j
−j
⎛
⎞⎛
⎞
3
p ( z ) = ( z + 1) ⎜ z − e ⎟⎜ z − e 3 ⎟⎜ z − e 4 ⎟⎜ z − e 4 ⎟
⎠⎝
⎠
⎝
⎠⎝
⎠⎝
(
)
p ( z ) = ( z + 1) ( z 2 − z + 1) z 2 + 2 z + 1
p ( z ) = z5 + 2z 4 + z3 + z 2 + 2z + 1
Nivel del lóbulo principal y secundarios
El lóbulo principal se encuentra en z=1.
Los lóbulos secundarios se encuentran aproximadamente en el punto
medio entre los dos nulos. La posición de los mismos está
aproximadamente en
π 3π
+
4
ψ1 = 3
2
ψ2 =
π+
2
3π
4
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
4
Se puede particularizar el polinomio de la agrupación en los puntos
z 1 = e j ψ1
z 2 = e j ψ2
También se puede sustituir el ángulo en la expresión del factor de
array
FA (ψ ) = 2 cos
ψ
2
+ 2 2 cos
3ψ
5ψ
+ 2 cos
2
2
Los lóbulos secundarios están son 11 dB y 23 dB inferiores al
principal.
El diagrama es
0
0
10
20 ⋅log( f ( θ ) )
20
− 30 30
0
0
1
2
θ
3
π
Diseño de una red de distribución
El polinomio es
p ( z ) = z5 + 2z 4 + z3 + z 2 + 2z + 1
Es necesario obtener niveles de potencia proporcionales a 1:2:1:1:2:1 .
Partiendo de un nivel 8, llegamos a niveles 4 por división de potencia
y a niveles 2 por una nueva división. Es necesario reordenar los
niveles de acuerdo con la secuencia.
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia