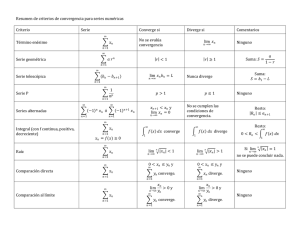
CRITERIOS PARA EL ESTUDIO DE LA CONVERGENCIA DE SERIES

CRITERIOS PARA EL ESTUDIO DE LA CONVERGENCIA DE SERIES
SERIES CON TÉRMINOS POSITIVOS
PROPIEDADES
∞
P
Si
an converge, entonces lim an = 0.
n→∞
n=1
TIPOS DE SERIES
GEOMÉTRICA
∞
P
Sea
(arn ), se verifica que
n=0
i) Si 0 < |r| < 1, entonces la serie converge a
ii) Si |r| ≥ 1, entonces la serie diverge.
a
.
1−r
ARMÓNICA
∞ 1
P
La serie
es divergente.
n=1 n
p–SERIE
∞ 1
P
, se verifica que
p
n=1 n
i) Si p > 1, entonces la serie converge.
ii) Si 0 ≤ p ≤ 1, entonces la serie diverge.
Sea
CRITERIOS
CRITERIO DE LA RAÍZ (DE CAUCHY)
√
Si existe lim n an = r se verifica que
n→∞
i) Si r < 1, entonces la serie converge.
ii) Si r > 1, entonces la serie diverge.
CRITERIO DEL COCIENTE (DE D’ALAMBERT)
an+1
Si existe lim
= r se verifica que
n→∞ an
i) Si r < 1, entonces la serie converge.
ii) Si r > 1, entonces la serie diverge.
CRITERIO DE RAABE
¡
an+1 ¢
Si existe lim n 1 −
= r se verifica que
n→∞
an
i) Si r > 1, entonces la serie converge.
ii) Si r < 1, entonces la serie diverge.
CRITERIO DE COMPARACIÓN
Sean 0 ≤ an ≤ bn , ∀ n ∈ IN .
∞
∞
P
P
i) Si
bn converge, entonces
an converge.
ii) Si
n=1
∞
P
n=1
n=1
an diverge, entonces
∞
P
n=1
bn diverge.
CRITERIO DE COMPARACIÓN EN EL LÍMITE
∞
∞
¡ an ¢
P
P
= l con 0 < l < ∞. Entonces ambas series
an ,
bn
Sean an , bn > 0 y lim
n→∞ bn
n=1
n=1
convergen o divergen simultáneamente.
CRITERIOS DE SERIES DE NÚMEROS REALES
CRITERIO DE DIRICHLET
∞
P
Si
an es una serie con sumas parciales acotadas (Sn ≤ M, ∀ n ∈ IN ) y (bn )n∈IN es una
n=1
sucesión decreciente cuyo lı́mite es 0, entonces
∞
P
n=1
an bn es convergente.
CRITERIO DE ABEL
∞
P
Si la serie
an converge y la sucesión (bn )n∈IN es monótona convergente (b1 ≤ b2 ≤ . . .
n=1
o b1 ≥ b2 ≥ . . .), entonces
∞
P
n=1
an bn es convergente.
CRITERIO DE LAS SERIES ALTERNADAS (CRITERIO DE LEIBNIZ)
Sea an > 0, la serie alternada
i) lim an = 0.
n→∞
ii) an+1 ≤ an , ∀ n ∈ IN .
∞
P
(−1)n an converge siempre que se verifica
n=1