Document

Cálculo de Variable Real
Guía teórica – Series
Escuela de Ingeniería
Centro de Ciencia Básica
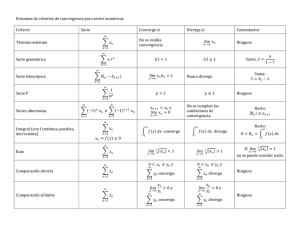
Series Infinitas:
Definición:
Sea {an} una sucesión infinita. La expresión a1 + a2 + … + an, se denomina serie infinita o serie y se denota
por:
+∞
{S n } = ∑ a n
n =1
S1 = a1
S2 = a1 + a2 = S1 + a1
S3 = a1 + a2 + a3 = S2 + a3
…
Sn = a1 + a2 + a3 + … + an = Sn-1 + an
Una serie es entonces, una sucesión de sumas parciales.
Definición de convergencia:
+∞
La serie infinita
∑a
n =1
n
converge si su sucesión de sumas parciales converge, es decir, Lim S n = S , para S
n → +∞
∈ ℜ, donde S es la suma de la serie infinita.
La serie infinita diverge si {Sn} diverge, en otras palabras, si el límite no existe entonces la serie diverge.
Existen dos formas para determinar la convergencia de una serie:
1. Encontrar Sn y luego evaluar el límite
2. Emplear los criterios de convergencia y unas series especiales:
Criterios de convergencia:
+∞
1. Si la serie infinita
∑a
n =1
n
converge, entonces Lim a n = 0 , el recíproco es falso. Pero si Lim a n ≠ 0 ,
n → +∞
n → +∞
+∞
entonces la serie infinita
∑a
n =1
+∞
2. Si
∑ an y
n =1
n
diverge.
+∞
∑ bn son convergentes y sus sumas son S1 y S2 respectivamente,
n =1
convergente y su suma es S1 ± S2.
+∞
3. Si
∑ an converge y
n =1
+∞
∑ bn diverge,
n =1
+∞
∑ (a
n =1
n
± bn ) diverge.
+∞
∑ (a
n =1
n
± bn ) es
+∞
4. Si
+∞
∑ an diverge y
∑ bn diverge,
n =1
n =1
+∞
5. Si
∑ an converge y
n =1
+∞
6. Si
+∞
∑ (a
n =1
n
± bn ) diverge o converge.
+∞
∑ bn con (an = bn ∀n ≥ m), entonces
n =1
+∞
∑ an diverge y
∑ bn con (an = bn ∀n ≥ m), entonces
n =1
n=m
7. Para cualquier N ∈ ℵ, las series:
+∞
∑a
n =1
n
+∞
∑b
n=m
n
converge.
+∞
∑b
n=m
n
diverge.
+∞
∑a
= a1 + a2 + ... + a N y
n = N +1
n
= a N +1 + a N + 2 + ... son ambas
convergentes o ambas divergentes.
+∞
8. Si la serie
∑a
n =1
+∞
n
es convergente y su suma es S, entonces la serie
∑ ka
n =1
n
con k ≠ 0 es convergente y
su suma es kS.
+∞
9. Si la serie
∑ bn es divergente, entonces
n=m
+∞
∑ kb
n =m
n
es divergente
Series especiales:
1. Serie telescópica o retráctil: Es aquella en la cual su término enésimo se puede descomponer en
fracciones parciales.
+∞
2. Serie armónica: Es de la forma
1
1
1
1
∑ n = 1 + 2 + 3 + 4 + ... donde a
n =1
n
=
1
n
Analizando su convergencia o divergencia:
{an } = 1, 1 , 1 , 1 ,... . De donde:
 2 3 4

a1 = 1
a2 = 1.5
a3 = 1.83
a4 = 2.083
{S n } = {1,1.5,1.83,2.083,...}
1
= 0 y con este criterio no podríamos concluir algo sobre la convergencia o
n → +∞ n
Evaluando: Lim
divergencia de la serie.
Por otra parte, Lim S n = +∞ , por lo tanto se concluye que la serie armónica diverge.
n → +∞
3. Serie geométrica: Es de la forma {S n } =
+∞
+∞
n =0
n =1
∑ ar n = ∑ ar n−1 = a + ar + ar 2 + ... + ar n−1 , donde a ≠ 0 se
llama primer término de la serie y r se llama razón.
Analizando su convergencia y / o divergencia, tenemos:
+∞
∑ ar
= a + ar + ar 2 + ... + ar n
n
n =0
(
)
(
Lim a + ar + ar 2 + ... + ar n = Lim a 1 + r + r 2 + ... + r n
n → +∞
n → +∞
)
(1 − r ) = (1 − r )(1 + r + r + ... + r )
(1 − r ) = 1 + r + r + ... + r
n
n −1
2
n
n −1
2
(1 − r )
(1 − r ) = 1 + r + r
n +1
(1 − r )
(
2
+ ... + r n
)
Lim a 1 + r + r 2 + ... + r n = Lim a
n → +∞
n → +∞
(1 − r ) =
n +1
(1 − r )
+∞
conclusión, la serie geométrica
∑ ar
n
(
)
[
]
a
a
a
Lim 1 − r n +1 =
1 − Lim r n +1 =
si r < 1 En
(1 − r ) n→+∞
(1 − r ) n→+∞
(1 − r )
converge si r < 1 y su suma es S = Lim S n =
n → +∞
n =0
a
siendo a el
(1 − r )
primer término y r la razón de la expresión. Si r ≥ 1 la serie es divergente.
+∞
∑n
4. Serie hiperarmónica o serie P: Es de la forma
n =1
1
p
. La serie es convergente si p > 1 y es divergente
si p ≤ 1.
Series de términos positivos:
Definición:
Si todos los términos de una serie infinita son positivos, entonces la sucesión de sumas parciales es
creciente.
Teorema:
Una serie infinita de términos positivos es convergente sii su sucesión de sumas parciales tiene una cota
superior.
Criterios de convergencia:
+∞
Sean
+∞
∑ an y
∑b
n
n =1
+∞
i.
Si
dos series de términos positivos.
n =1
∑b
n
converge y bn ≥ an ∀n, entonces
n =1
+∞
ii.
Si
∑
n =1
bn diverge y an ≥ bn ∀n, entonces
+∞
∑a
n =1
n
también converge
+∞
∑a
n =1
n
también diverge.
Nota: Si se da otro caso, no se puede concluir nada con este criterio.
Criterio de comparación del límite:
+∞
Sean
∑ an y
n =1
+∞
a 
dos series de términos positivos, entonces si el límite: L = Lim  n  existe y 0 < L < +∞,
n → +∞ b
 n
∑b
n
n =1
entonces ambas series convergen o ambas series divergen.
Notas:
•
•
a 
Si Lim  n  = 0 y
n → +∞ b
 n
+∞
+∞
∑
bn converge,
a 
Si Lim  n  = +∞ y
n → +∞ b
 n
∑a
n =1
n =1
n
converge.
n
diverge.
+∞
+∞
∑b
n
diverge,
∑a
n =1
n =1
Criterio de la integral:
Si f es una función continua, de valor positivo y decreciente ∀x ≥ 1. Si
positivos y f(n) = an ∀n ≥ 1, entonces la serie
∑a
∑a
n
es una serie de términos
+∞
n
∫ f (x )dx
converge y la integral impropia
convergen
1
ambas o divergen ambas.
Teorema:
Si la serie
∑
+∞
an y la integral
∫ f (x )dx
satisfacen la hipótesis del criterio de la integral y convergen,
1
+∞
∫
f (x )dx ≤ Rn ≤
n +1
+∞
∫ f (x )dx
donde Rn = S – Sn y se conoce como residuo o error de truncamiento.
n
Series alternantes:
Definición:
+∞
Es
una
serie
infinita
de
la
forma
∑ (− 1)
n +1
an = a1 − a2 + a3 − a4 + a5 − ...
n =1
+∞
∑ (− 1) a
n
n
= − a1 + a2 − a3 + a4 − a5 + ... , donde an >0 ∀n.
n =1
Criterio de la serie alternante:
Si an ≥ an+1 > 0 ∀n y Lim an = 0 , entonces la serie dada converge.
n→+∞
o
de
la
forma:
Estimación del error de una serie alternante:
Sea una serie alternante convergente. Sea S la suma de la serie. Denotamos con Rn = S – Sn el error
obtenido al aproximar la suma de la serie mediante la suma parcial Sn, entonces S − S n = Rn ≤ an +1
Convergencia absoluta:
Definición:
+∞
La serie
∑
+∞
an es absolutamente convergente (AC) si
n =1
∑a
n
es convergente.
n =1
Si una serie es convergente pero no es absolutamente convergente, se dice que es condicionalmente
convergente (CC).
Se emplean los siguientes criterios de convergencia:
Criterio de la razón o del cociente:
+∞
∑a
Si
n
es una serie infinita con an ≠ 0, ∀n ∈ ℵ, entonces si:
n =1
i.
Lim
an+1
= L < 1 , la serie es AC.
an
Lim
an+1
= L > 1 , la serie diverge (D).
an
Lim
an+1
= 1 , nada se puede concluir
an
n →+∞
ii.
n→+∞
iii.
n →+∞
Criterio de la raíz:
+∞
∑a
Si
n
es una serie infinita con an ≠ 0, ∀n ∈ ℵ, entonces si:
n =1
Lim n an = L < 1 , la serie es AC.
i.
n→+∞
Lim n an = L > 1 , la serie diverge (D).
ii.
n →+∞
Lim n an = 1 , nada se puede concluir
iii.
n→+∞
Series de potencia:
Definición:
Sea x ∈ ℜ. Se llama serie de potencia de x – c (o centrada en c) a una serie de la forma:
+∞
∑ a (x − c )
n
n
n =0
= a0 + a1 ( x − c ) + a2 ( x − c ) + a3 ( x − c ) + ... + an ( x − c ) con (x – c)0 = 1.
2
3
n
+∞
Si c = 0, la serie queda de la forma:
∑a x
n
n
= a0 + a1 x + a2 x 2 + a3 x 3 + ... + an x n .
n =0
En algunas ocasiones c = φ(x), es decir, una función de variable x, así:
+∞
∑ a [φ (x )]
n
n
n =0
Teorema de convergencia de series de potencia:
∑ a (x − c )
n
Si
n
es una serie de potencias, entonces:
i.
La serie converge ∀x ∈ ℜ
ii.
La serie converge cuando x = c
iii.
Existe un número R > 0 de modo que la serie es absolutamente convergente si x − c < R y diverge
si x − c > R . En donde R se llama radio de convergencia y al conjunto de valores de x se llama
intervalo de convergencia.
Para determinar el radio de convergencia de una serie de potencias, se utilizan los criterios de la razón y de
la raíz bajo las siguientes condiciones:
•
Si L = 0, la serie converge ∀x ∈ ℜ
•
Si L = +∞, la serie converge solo en x = c
•
Si L > 0, la serie converge ∀x tal que x − c < L
Nota: Las aplicaciones de las series de potencia están en:
•
Calcular aproximaciones de los números irracionales, por ejemplo: , e, π, Ln(0.3), sen(0.4), etc.
•
Hallar el valor aproximado de una integral definida cuyo integrando tiene una derivada que no puede
π
0.5
expresarse en términos de funciones elementales, es decir:
∫
0
t2
e dt ,
4
∫ cos
x dx .
0
Operaciones con series de potencia:
Sea f ( x ) =
+∞
∑
an x n y g ( x ) =
n =0
+∞
∑b x
n
n
para x < R , entonces:
n =0
a) f ( x ) ± g (x ) =
+∞
∑ (a
n
± bn )x n
n=0
b) f ( x )g ( x ) = a0b0 + (a0b1 + a1b0 )x + (a0b2 + a1b1 + a2b0 )x 2 + ...
c)
Sea
f (x )
se obtiene por división sucesiva con g ( x ) ≠ 0
g (x )
f (x ) =
+∞
∑ a (x − c )
n
n
una serie de potencias con R > 0, continua, derivable y con intervalo de
n=0
convergencia (c – R, c + R), entonces:
a)
b)
+∞
d +∞
n
n −1
an ( x − c ) = an n( x − c )
dx n = 0
n=0
∑
f ´( x ) =
∫
+∞
∫∑
f ( x )dx =
∑
an ( x − c ) dx =
n
n=0
+∞
∑∫
an (x − c ) dx =
n
n =0
an ( x − c )
n +1
n=0
n +1
+∞
∑
+c
Nota: En f ´( x ), f ( x )dx , el radio de convergencia sigue siendo R > 0, pero en el intervalo de convergencia
∫
los extremos pueden variar.
Representación de funciones mediante series de potencias:
1. Series de potencias geométricas:
Si f ( x ) =
+∞
∑ ar
n
a
, r <1
1− r
=
n=0
+∞
Si hacemos r = x,
∑ ax
n =0
n
=
a
, x <1
1− x
Observaciones:
•
a
n
+∞
a
−a
b = − a  x  (Centrada en cero)
=
=
x−b b− x  x
b n=0  b 
1 − 
 b
•
a
n
+∞
a
a
a
−a
 x−c
b−c = − a
=
=
=
=
 (Centrada en c)

b − c n=0  b − c 
x − b x − c − b + c ( x − c ) − (b − c ) (b − c ) − (x − c )  x − c 

1 −
 b−c 
−
∑
−
∑
En ambos casos el radio de convergencia es R = b − c
2. Serie de Taylor:
f (x ) =
+∞
∑c x
n
n
= c0 + c1 x + c2 x 2 + c3 x 3 + ... + cn x n + ...
n =0
f (x ) =
+∞
∑ c (x − a )
n
n
= c0 + c1 ( x − a ) + c2 ( x − a ) + c3 (x − a ) + ... + cn ( x − a ) + ... (1)
2
3
n
n =0
Cuyo radio de convergencia es R > 0
Existen derivadas de diferentes órdenes en (a – R, a + R):
f ´( x ) = c1 + 2c2 (x − a ) + 3c3 (x − a ) + 4c4 ( x − a ) + ... + ncn ( x − a )
2
n −1
3
f ´´( x ) = 2c2 + 6c3 (x − a ) + 12c4 (x − a ) ... + n(n − 1)cn (x − a )
n−2
2
+ ...
+ ...
f ´´´(x ) = 6c3 + 24c4 ( x − a ) + 2 × 3 × 4 × 5c5 ( x − a ) + ... + n(n − 1)(n − 2 )cn ( x − a )
3
…
n −3
+ ...
Si x = a:
f (a ) = c0
f ´(a ) = c1
f ´´(a ) = 2c2
f ´´´(a ) = 2 × 3c3 = 6c3
M
f (n ) (a ) = 2 × 3 × 4 × ... × ncn ⇒ cn =
f (n ) (a )
n!
(2)
Reemplazando (2) en (1):
f (x ) =
+∞
∑
n =0
f (n ) (a )
(x − a )n (Serie de Taylor centrada en a)
n!
Observaciones:
•
Si en la serie de Taylor hacemos a = 0, obtenemos la serie de Maclaurin: f ( x ) =
+∞
∑
n =0
•
f (n ) (0 ) n
x .
n!
La representación de una función mediante series de potencias es única
3. Serie Binomial:
Del teorema del binomio se tiene:
(a + b )m = a m + ma m +1b + m(m − 1)a
m(m − 1)(m − 2 )a m −3 b 3
m(m − 1)(m − 2 )...(m − (k − 1))a m − k b k
+ ... +
+ ... + b m
2!
3!
k!
Si hacemos: a = 1, b = x, m ∈ Q, entonces:
(1 + x )m = 1 + mx + m(m − 1)x
+∞
(1 + x )m = 1 + ∑
n =1
m −2
b2
+
m(m − 1)(m − 2 )x 3
m(m − 1)(m − 2 )...(m − (k − 1))x k
+ ... +
+ ... + x m
2!
3!
k!
m(m − 1)(m − 2 )...(m − n + 1)x n
n!
2
+
Otra forma de tener la serie binomial es:
f ( x ) = (1 + x ) =
k
+∞
∑
n =0
f ´( x ) = k (1 + x )
k −1
f (n ) (x )x n
⇒ f (0 ) = 0
n!
⇒ f ´(0 ) = k
f ´´( x ) = k (k − 1)(1 + x )
k −2
⇒ f ´´(0 ) = k (k − 1)
f ´´´( x ) = k (k − 1)(k − 2)(1 + x )
k −3
⇒ f ´´´(0 ) = k (k − 1)(k − 2 )
M
f (x ) =
+∞
∑
n =0
f (n ) (x )x n
= f
n!
k
+∞
∑
n =1
(0) + f ´(0)x +
f ´´(0 )x 2
f ´´´(0 )x 3
+
+ ...
2!
3!
k (k − 1)x 2 k (k − 1)(k − 2 )x 3
+
+ ...
2!
3!
k (k − 1)(k − 2 )...(k − n + 1)x n
n!
f ( x ) = (1 + x ) = 1 + kx +
f (x ) = 1 +
0