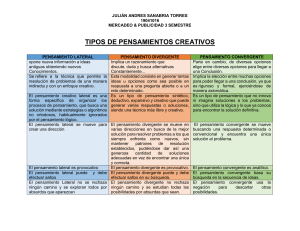
SERIES INFINITAS DE TÉRMINOS POSITIVOS Y NEGATIVOS
Anuncio

SERIES INFINITAS DE TÉRMINOS POSITIVOS Y NEGATIVOS Definición. Si para todo entero positivo , entonces la serie: Y la serie Son series alternas o alternantes. Teorema (I). Si los números serie alterna son alternadamente positivos y negativos, para todo entero positivo y , entonces la es convergente. Ejemplo: Determinar si la serie es convergente o divergente. Planteamos los elementos : Aplicamos el teorema: se cumple Determinamos el límite al infinito de : También se cumple. Luego, la serie es convergente Definición. convergente. es absolutamente convergente si Teorema (II). PRUEBA DE LA RAZÓN. Sea una serie infinita dada para toda (i) Si es diferente de cero, entonces: la serie dada es absolutamente convergente. (ii) Si ó si la serie es divergente. (iii) Si no se puede concluir. Ejemplo: Determine si es convergente o divergente. Aplicando la prueba de la razón tenemos: La serie es absolutamente convergente PARA VOLVER AL MENÚ ANTERIOR PRESIONE Series y Sucesiones EN EL MENU PRINCIPAL