La figura 2.3 ilustra el concepto de funciуn de distribuciуn
Anuncio
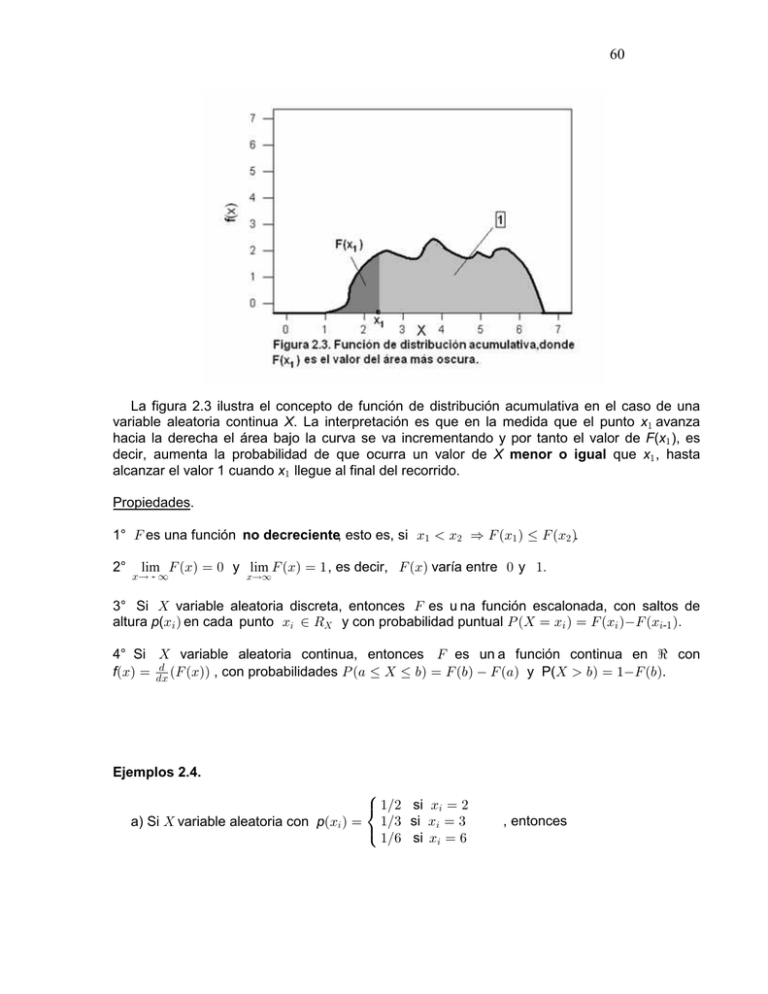
60 La figura 2.3 ilustra el concepto de función de distribución acumulativa en el caso de una variable aleatoria continua X. La interpretación es que en la medida que el punto x" avanza hacia la derecha el área bajo la curva se va incrementando y por tanto el valor de F(x" ), es decir, aumenta la probabilidad de que ocurra un valor de X menor o igual que x" , hasta alcanzar el valor 1 cuando x" llegue al final del recorrido. Propiedades. 1° J es una función no decreciente, esto es, si B" B# Ê J ÐB" Ñ Ÿ J ÐB# Ñ. 2° lim J ÐBÑ œ ! y lim J ÐBÑ œ " , es decir, J ÐBÑ varía entre ! y "Þ BÄ - _ BÄ_ 3° Si \ variable aleatoria discreta, entonces J es u na función escalonada, con saltos de altura p(B3 Ñ en cada punto B3 − V\ y con probabilidad puntual T Ð\ œ B3 Ñ œ J ÐB3 ÑJ ÐB3-" ÑÞ 4° Si \ variable aleatoria continua, entonces J es un a función continua en d con . fÐBÑ œ .B ÐJ ÐBÑÑ , con probabilidades T Ð+ Ÿ \ Ÿ ,Ñ œ J Ð,Ñ J Ð+Ñ y P(\ ,Ñ œ "J Ð,Ñ. Ejemplos 2.4. Ú "Î# si B œ # 3 a) Si \ variable aleatoria con pÐB3 Ñ œ Û "Î$ si B3 œ $ Ü "Î' si B3 œ ' , entonces











