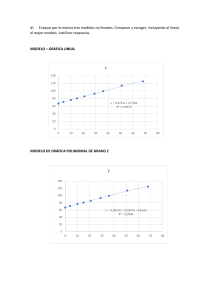
GraficasNro 01 math1

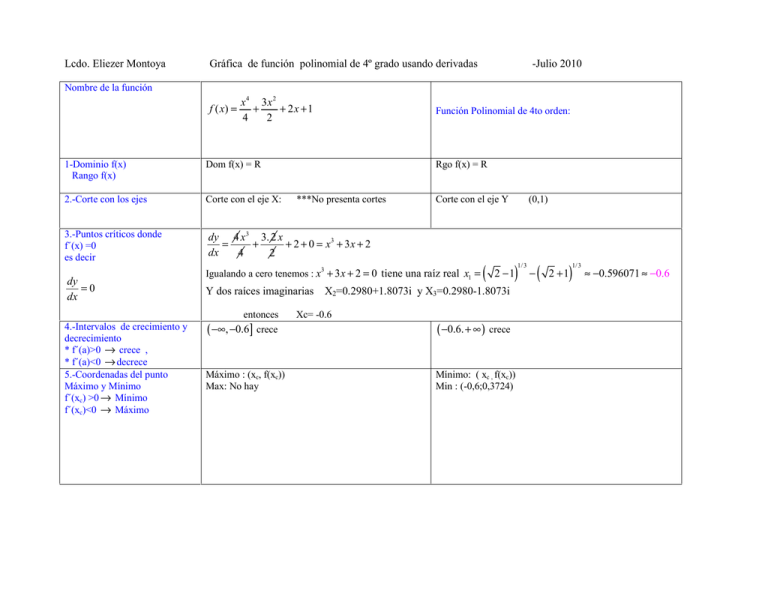
Lcdo. Eliezer Montoya
Gráfica de función polinomial de 4º grado usando derivadas
-Julio 2010
Nombre de la función
f ( x) =
x 4 3x 2
+
+ 2x +1
4
2
Función Polinomial de 4to orden:
1-Dominio f(x)
Rango f(x)
Dom f(x) = R
2.-Corte con los ejes
Corte con el eje X:
3.-Puntos críticos donde
f´(x) =0
es decir
dy 4 x 3 3. 2 x
=
+
+ 2 + 0 = x3 + 3x + 2
dx
4
2
dy
=0
dx
***No presenta cortes
Corte con el eje Y
Igualando a cero tenemos : x3 + 3 x + 2 = 0 tiene una raíz real x1 =
Y dos raíces imaginarias
entonces
4.-Intervalos de crecimiento y
decrecimiento
* f´(a)>0 → crece ,
* f´(a)<0 → decrece
5.-Coordenadas del punto
Máximo y Mínimo
f´(xc) >0 → Mínimo
f´(xc)<0 → Máximo
Rgo f(x) = R
(
(0,1)
1/ 3
) −(
2 −1
X2=0.2980+1.8073i y X3=0.2980-1.8073i
Xc= -0.6
( −∞, −0.6] crece
( −0.6. + ∞ ) crece
Máximo : (xc, f(xc))
Max: No hay
Mínimo: ( xc , f(xc))
Min : (-0,6;0,3724)
1/ 3
)
2 +1
≈ −0.596071 ≈ −0.6
Lcdo. Eliezer Montoya
Gráfica de función polinomial de 4º grado usando derivadas
6.-Puntos de inflexión
f´´(x) = 0
f´´(x)>0 → cóncava hacia arriba
f´´(x)<0 → cóncava hacia abajo
d2y
= 3 x 2 + 3 podemos ver que no posee solución
2
dx
7.-Asintotas.
real, en este caso son imaginarias
0 = 3 x 2 + 3 ⇒ x = −3 / 3 = −1 = i
d2y
= f ´´(−0.6) = 3(−0, 6)2 + 3 = 4, 08 > 0
2
dx
d2y
= f ´´(−1) = 3(−1)2 + 3 = 6 > 0
2
dx
No presenta asintotas
-Julio 2010
Cóncava hacia arriba pues la segunda derivada es positiva
Lcdo. Eliezer Montoya
Gráfica de función polinomial de 4º grado usando derivadas
Vista general de la grafica solicitada
Aplicando un ZOOM … podemos observar
-Julio 2010
Lcdo. Eliezer Montoya
Gráfica de función polinomial de 4º grado usando derivadas
-Julio 2010