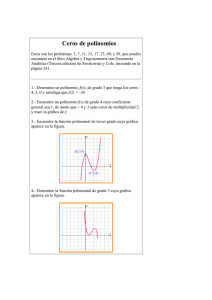
Hoja de Trabajo Funciones Polinómicas: Grado, Factores, Interceptos
Anuncio

Guía de Matemática LICEO EL ARRAYÁN UNIDAD TÉCNICA PEDAGÓGICA DEPARTAMENTO DE MATEMATICA Tema: Función Polinomial Profesor: Alan Carrasco C. Nombre: ___________________________________________________ Curso: 4º Diferenciado Fecha: ____ / ____ / 2019 Objetivo: Comprender el concepto de función polinomial reconociendo sus características. Representar gráficamente una función polinomial Capacidad: Comprender, Aplicar y Analizar. FUNCIÓN POLINOMIAL Sea n un número entero no negativo y sean 𝑎𝑛 , 𝑎𝑛−1 … 𝑎2 , 𝑎1 , 𝑎0 números reales con 𝑎𝑛 ≠ 0. Definiremos una función polinomial f de grado n como aquella de la forma: 𝒇(𝒙) = 𝒂𝒏 𝒙𝒏 + 𝒂𝒏−𝟏 𝒙𝒏−𝟏 + ⋯ + 𝒂𝟐 𝒙𝟐 + 𝒂𝟏 𝒙 + 𝒂𝟎 DOMINIO Y RECORRIDO DE LA FUNCIÓN POLINOMIAL Su dominio serán siempre todos los reales (ℝ). Su recorrido dependerá de si su exponente es impar (todos los reales) o par (depende del máximo o mínimo). EJEMPLO 1: Con respecto a la función polinomial 𝒙𝟑 − 𝟐𝒙𝟐 − 𝒙 + 𝟐, responde las siguientes preguntas: ¿Cuál es el grado? ¿Cuál es el coeficiente principal? ¿Cuál es término libre? ¿Cuál es el conjunto de las posibles soluciones para factorizar dicha función? ¿Cuál de los siguientes valores es un factor del polinomio? a) – 1 b) + 1 c) – 2 d) 2 ¿Cuáles son las intersecciones con el eje X? ¿Cuáles son las intersecciones con el eje y? CARACTERÍSTICAS GENERALES DEL GRÁFICO DE UNA FUNCIÓN POLINOMIAL f es una función continua, es decir, su gráfica no tiene interrupciones, cortes o saltos. La gráfica de f es una curva suave con esquinas redondeadas y sin esquinas agudas La gráfica de f interseca al eje x en máximo n puntos La gráfica de f tiene como máximo n – 1 puntos en donde cambia de dirección. La grafica interseca al eje Y en un punto (𝟎, 𝒂𝟎 ) Las dos ramas van a los positivos o a los negativos RAMAS DE LA FUNCIÓN a) Si an>0 y n es par, ambas ramas se dirigen al infinito positivo b) Si an>0 y n es impar, ambas ramas se dirigen al infinito negativo- Actividad Nº1 Instrucciones: Determina la parte real e imaginaria de los siguientes números complejos. Con respecto a la función polinomial 𝒙𝟑 + 𝒙𝟐 − 𝟒𝒙 + 𝟒, responde las siguientes preguntas: ¿Cuál es el grado? ¿Cuál es el coeficiente principal? ¿Cuál es término libre? ¿Cuál es el conjunto de las posibles soluciones para factorizar dicha función? ¿Cuál de los siguientes valores es un factor del polinomio? a) – 1 b) +1 c) – 2 d) 2 ¿Cuáles son las intersecciones con el eje X? ¿Cuáles son las intersecciones con el eje y?