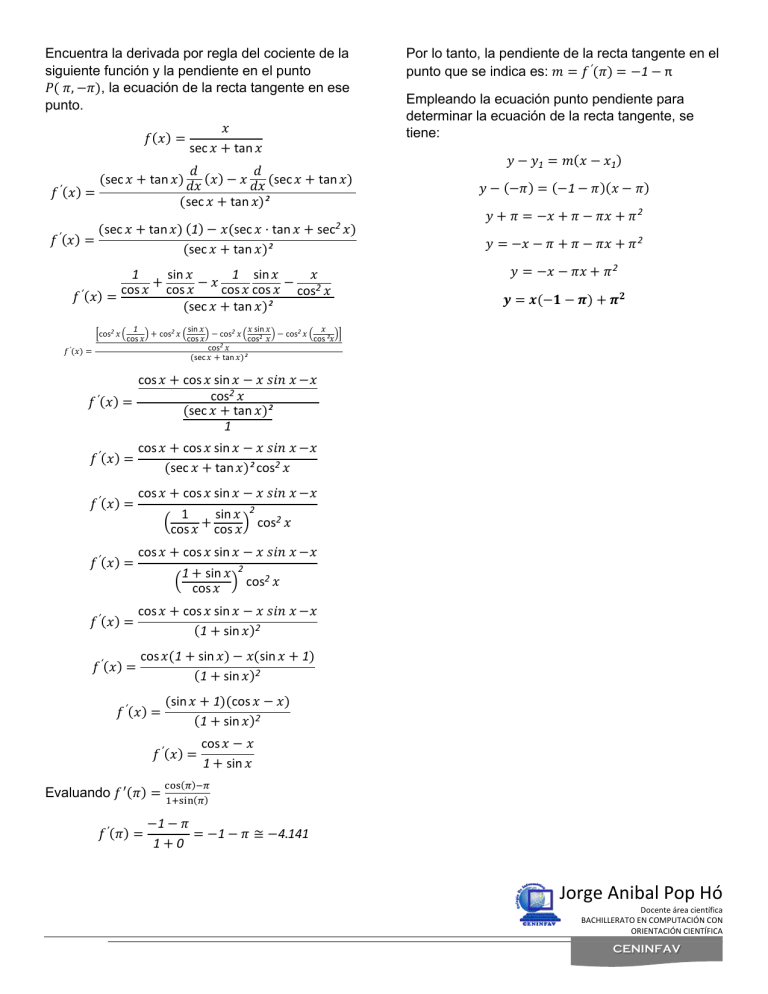
Encuentra la derivada por regla del cociente de la siguiente función y la pendiente en el punto 𝑃( 𝜋, −𝜋), la ecuación de la recta tangente en ese punto. 𝑓(𝑥) = 𝑥 sec 𝑥 + tan 𝑥 𝑑 𝑑 (sec 𝑥 + tan 𝑥) (𝑥) − 𝑥 (sec 𝑥 + tan 𝑥) 𝑑𝑥 𝑑𝑥 𝑓 ′ (𝑥) = (sec 𝑥 + tan 𝑥)² 2 𝑓 ′ (𝑥) = (sec 𝑥 + tan 𝑥) (1) − 𝑥(sec 𝑥 · tan 𝑥 + sec 𝑥) (sec 𝑥 + tan 𝑥)² 1 sin 𝑥 1 sin 𝑥 𝑥 + cos 𝑥 − 𝑥 cos 𝑥 cos 𝑥 − 2𝑥 cos 𝑥 cos 𝑓 ′ (𝑥) = (sec 𝑥 + tan 𝑥)² [cos2 𝑥 ( 𝑓 ′(𝑥) = Por lo tanto, la pendiente de la recta tangente en el punto que se indica es: 𝑚 = 𝑓 ′ (𝜋) = −1 − π Empleando la ecuación punto pendiente para determinar la ecuación de la recta tangente, se tiene: 𝑦 − 𝑦1 = 𝑚(𝑥 − 𝑥1 ) 𝑦 − (−𝜋) = (−1 − 𝜋)(𝑥 − 𝜋) 𝑦 + 𝜋 = −𝑥 + 𝜋 − 𝜋𝑥 + 𝜋 2 𝑦 = −𝑥 − 𝜋 + 𝜋 − 𝜋𝑥 + 𝜋 2 𝑦 = −𝑥 − 𝜋𝑥 + 𝜋 2 𝒚 = 𝒙(−𝟏 − 𝝅) + 𝝅𝟐 1 sin 𝑥 𝑥 sin 𝑥 𝑥 ) + cos2 𝑥 ( ) − cos2 𝑥 ( 2 ) − cos2 𝑥 ( )] cos 𝑥 cos 𝑥 cos ²𝑥 cos 𝑥 cos2 𝑥 (sec 𝑥 + tan 𝑥)² cos 𝑥 + cos 𝑥 sin 𝑥 − 𝑥 𝑠𝑖𝑛 𝑥 −𝑥 cos2 𝑥 𝑓 ′ (𝑥) = (sec 𝑥 + tan 𝑥)² 1 𝑓 ′ (𝑥) = 𝑓 ′ (𝑥) = 𝑓 ′ (𝑥) = cos 𝑥 + cos 𝑥 sin 𝑥 − 𝑥 𝑠𝑖𝑛 𝑥 −𝑥 (sec 𝑥 + tan 𝑥)² cos2 𝑥 cos 𝑥 + cos 𝑥 sin 𝑥 − 𝑥 𝑠𝑖𝑛 𝑥 −𝑥 1 sin 𝑥 2 ( + ) cos2 𝑥 cos 𝑥 cos 𝑥 cos 𝑥 + cos 𝑥 sin 𝑥 − 𝑥 𝑠𝑖𝑛 𝑥 −𝑥 1 + sin 𝑥 2 ( cos 𝑥 ) cos2 𝑥 𝑓 ′ (𝑥) = cos 𝑥 + cos 𝑥 sin 𝑥 − 𝑥 𝑠𝑖𝑛 𝑥 −𝑥 (1 + sin 𝑥)2 𝑓 ′ (𝑥) = cos 𝑥(1 + sin 𝑥) − 𝑥(sin 𝑥 + 1) (1 + sin 𝑥)2 𝑓 ′ (𝑥) = (sin 𝑥 + 1)(cos 𝑥 − 𝑥) (1 + sin 𝑥)2 𝑓 ′ (𝑥) = Evaluando 𝑓 ′ (𝜋) = 𝑓 ′ (𝜋) = cos 𝑥 − 𝑥 1 + sin 𝑥 cos(𝜋)−𝜋 1+sin(𝜋) −1 − 𝜋 = −1 − 𝜋 ≅ −4.141 1+0 Jorge Anibal Pop Hó Docente área científica BACHILLERATO EN COMPUTACIÓN CON ORIENTACIÓN CIENTÍFICA CENINFAV Jorge Anibal Pop Hó Docente área científica BACHILLERATO EN COMPUTACIÓN CON ORIENTACIÓN CIENTÍFICA CENINFAV









