3 Trayectorias ortogonales y sus aplicaciones

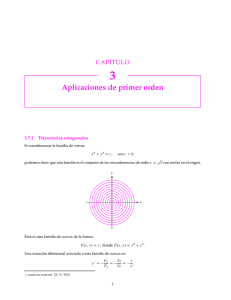
3 Trayectorias ortogonales y sus aplicaciones
Suponga que nos dan una familia de curvas como en la
Figura 3.16 (líneas gruesas). Podemos pensar en otras
familia de curvas (líneas puxiteadas) tal que cada miembro
de esta familia corte a cada miembro de la primera familia en
ángulos rectos. Por ejemplo, la curva AB se encuentra con
varios miembros de la familia punteada en ángulos rectos en
los puntos L, M, N, O, P. Decimos que las ‘familias son
mutuamente ortogonales, o que una forma un conjunto de
trayectorias ortogonales de la otra familia. Como una
ilustración, considere la familia de todos los círculos con
centro en el origen; unos cuantos círculos aparecen en, la
Figura 3.17. Las trayectorias ortogonales para esta familia de
círculos podrían ser miembros de la familia de las
Y
Figura
3.16
,
Figura 3.17
líneas rectas (líneas punteadas). Similarmente las trayectorias
ortogonales de la familia de líneas rectas que pasan por el origen
son los círculos con centro en el origen.
Como una situación más complicada, considere la familia de
elipses (Fi-gura 3.18) y la familia de curvas ortogonales a ellas. Las
curvas de una familia son las trayectorias ortogonales de la otra familia
. Las aplicaciones de trayectorias ortogonales son numerosas en fisica
e ingeniería. Como una aplicación muy elemental, considere la Figura
3.19. Aquí NS representa una barra magnética, siendo N su polo norte,
y S su polo sur. Si limaduras de hierro se esparcen alrededor del
magneto encontramos que ellas se ordenan así mismas como las
curvas punteadas de la Figura 3 . 19 . Estas curvas se llaman líneas
de fuerza.* Las curvas perpendiculares a estas (líneas gruesas) se
*El estudiante que ha leído la sección direcciones (pág. 28)
de campos de similitud entre las limaduras debería notar la linea.
de hierro y los elementos de linea
Capítulo tres
Figura 3.18
Figura 3.19
llaman líneas equipotenciales, o curvas de igual potencial. Aquí,
también los miembros de una familia constituyen las trayectorias
ortogonales de la otra familia.
Como otro ejemplo de física considere la Figura 3.20, la cual
representa un mapa del clima tan familiar en muchos de nuestros
periódicos diarios. Las curvas representan isobaras, las cuales son
curvas que conectan todas las ciudades que reportan la misma
presión barométrica a la oficina metereo-lógica. Las trayectorias
ortogonales de la familia de isobaras podrían indicar
la dirección general del viento desde áreas de alta a baja presión. En vez
de , isobaras, la Figura 3.20 podría representar curvas isotérmicas las
cuales son curvas que conectan puntos que tienen la misma temperatura.
En tal caso
las trayectorias ortogonales representan la dirección general del
flujo de calor. Considere el ejemplo de las isobaras. Dado un
punto (x, y), teóricamente podemos encontrar la presión en ese punto. Así podemos
decir que P= f(r, y), esto es, la presión es una función de la
posición. Haciendo P igual a u n v a l o r d e f i n i d o , d i g a m o
s P,, vemos que f(n, y) = P, representa una
Aplicaciones
primer
de
orden
ecuaciones diferenciales de
y simples de
orden superior 91
Figura 3 . 20
curva, todos los puntos que tienen presión P, siendo así una isobara.
Dan-do otros valores a P, se obtienen otras isobaras. Es claro que
estas isobaras no se podrían intersectar, puesto que si lo hicieran,
entonces los puntos de intersección tendrían dos presiones diferentes,
y esto sería imposible. Si usamos c en vez de P vemos que
f(-% Y) = c
(1)
donde c puede tomar valores dentro de un conjunto dado, representa
una fa-milia de isobaras. En el primer capítulo aprendimos cómo
encontrar una ecuación diferencial para una familia de curvas
derivando hasta eliminar las constantes arbitrarias (c en nuestro
caso). El problema que enfrentamos ahora es cómo obtener la familia
de trayectorias ortogonales. Realmente esto es sencillo puesto que la
ecuación diferencial de la familia (1) está dada por
af
af
dy
af/ax
df=xdx+ãl;dy=O o
- = 3fm
dX
Ahora la pendiente de las trayectorias ortogonales debería ser el
recíproco negativo de la pendiente en (2), esto es,
afh
af1a.x
Así, la ecuación
diferencial
para
la
familia
de
trayectorias ortogonales es
dy afb
-=(3)
dx af1a.x
Al resolver esta ecuación se obtienen las trayectorias ortogonales.
Ahora se darán ,algunas ilustraciones al procedimiento., Un error
común de los estu-diantes es olvidarse de eliminar las constantes
arbitrarias al hallar la ecua-ción diferencial de la familia.
EJEMPLO
Encuentre las
+y” =
trayectorias
cx.
ILUSTRATIVO
ortogonales
1
de
Formulación matemática. Hay dos maneras de determinar la
ecua-ción diferencial de la familia.
92
Capítulo tres
x2
Primera manera. Resuelva c para obtener c = (x1 +yl
)/x. Derivando con respecto a x, tenemos
x(2.x +
\,, = 9 = j.’ 2JJ’)
- (2 + j,‘)(l) = 0 o x2
.
(1.
3.Y
Y2
X
)‘
Segunda manera.
x2 +J’” =cx c o n r e s p e c t o a
mos
2.Y + 2A.j.’
= (’
Derivando
x, encontra
Eliminando c entre esta última ecuación y la dada, encontramos la
ecuación como antes.
La familia de las trayectorias
ecuación diferen-
ortogonalestiene
así la
cial
dl2s \‘
-xn
(4)
(IX.Y - )‘
Solución Para resolver (4), note que es una ecuación homogénea.
Haciendo y = vx, el estudiante puede mostrar que 3~2 +yz = c ,y. La
solución tam-bién se obtiene al notar que (4), sin fracciones, tiene un
factor integrante de-pendiendo de una variable (l/y’ ).
Las dos familias ortogonales se muestran en la Figura 3.21. La
familia dada originalmente se muestra punteada .
Y
tx
Figura
EJEMPLO
ILUSTRATIVO
3.21
2
Encuentre las tra3;ectorias ortogonales de la familia y = x + ce- *
y de-termine aquel miembro particular de cada familia que pasa por
(0, 3).
Formulación matemática. Por diferenciación de la relación
dada te-nemos
)“ = 1 - (.e-*
Eliminando c
Aplicaciones
primer
3
da
de
orden
ecuaciones diferenciales de
y simples de
orden superior 9
Así,
la
ecuación
diferencialde la
trayectorias ortogonales es
-1
dy _
d- 1 + x u
J
SoluciónEscriba (5) en la forma dx
familia de
(5)
+ (1+x
-y)dy = 0.
así que la ecuación no es exacta. Ahora o - 1
no es una
función sólo de
1 + s -J
1-o
x. Pero - = 1 es una función de y. De donde CS ’ dg = e? es un
factor in-1
tegrante. Multiplicando por este factor y procediendo como de
costumbre pa-ra ecuaciones exactas, obtenemos
,\.“> - eJ’(
’
y
- 2) = (‘,
Las curvas referidas que pasan por (0, 3) son
!’ = s + 3&“, .y - ,’ + 2 + p3-J = 0
(6)
El estudiante lo puede encontrar instructivo obtener los gráficos de las
ecua-ciones (6). También lo puede encontrar instructivo resolver (5)
al escribirla como
$+x=?.l
una ecuación
lineal con x
dependiente.
como variable
EJERCICIOS A
La ecuación yz = cx define una fahilia de parábolas. (a) Encuentre
una ecuación diferencial para la familia. (b) Encuentre una ecuación
diferencial para las tra-yectorias ortogonales y resuelva. (c)
Grafique varios miembros de cada familia en el mismo conjunto de
ejes.
Encuentre las trayectorias ortogonales de la familia y.3 = cxï y
dibuje un gráfico de las familias.
Determine las trayectorias ortogonales de cada familia y
encuentre miembros par-ticulares de cada una que pasen por los
puntos indicados.
(a x
c
1:
(b) x2 c’y
(3. - (c) y = c tan 7.~ +
) 2 -t y = (2. I ).
=
+ y’:
1). 1: i.0
i !
Id
“ ?.
+ co:
(ej y2
x’) ( - 2.
) y = C ’ 3x: 3)
=
dl + :
5).
4. Muestre que
las familias xL + 4~” =
=
c,n-’ son ortogonales.
cI
y
y
EJERCICIOS B
Encuentre la constante (I para que las familias y.3 = c, x y ~2 +ay”
= CL sean ortogonales.
Muestre que la familia de parábolas 3” = 4cx + 4~’ es “así mismo
ortogonal”. Gra-fique algunos miembros.
3. Muestre que la
94
Capítulo
familia
tres
donde a y b son constantes dadas, es “así mismo ortogonal”. Esta
se llama una fa-milia de “cónicas confocales”. Grafique algunos
miembros de la familia.
Determine las trayectorias ortogonales de (a) .KP + cyp = 1; p =
constante, (b)xl + cxy +y’ = 1.
EJERCICIOSC
Determine la familia de curvas en la cual cada miembro de la familia
de líneas rectas y = mx
uno de sus miembros corta a cada a un ángulo de 45”.
Determine la curva que pasa por ($, x%??) y corta cada miembro de la
familia ~2 +y’ =cL a un ángulo de W.
Encuentre todas las curvas que cortan la familia y = CE” a un ángulo N
cons--.
tante.
4. Muestre que si
una
ecuación
diferencial de
una
familia de curvas
en
coordenadas
polares (r, @) está dada por
dr
- = F(r. 4)
(4
entonces
una ecuación
diferencial para la
familia de
trayectorias ortogonales es
,.2
(11.
-=--,
r/4’, F-tr. cp)
(Sugerencia: Use el resultado del cálculo elemental que en coordenadas
polares la tangente del ángulo formado por el radio vector y la línea
tangente a la curva es rd+/dr.)
Encuentre las trayectorias ortogonales de r = c cos 4 y grafique.
Determine las trayectorias ortogonales de las espirales r = erm
Encuentre las trayectorias ortogonales de la cardioide r = ~(1 cos 4).
Sea F(Z) = u (x, y) + io(x, 3,) donde z = x + ;y y las funciones u (x, y) y
1,1(x, y) son reales. (a) Encuentre u (x, y) y u(x, y) correspondiente a
F(z) = ~2 y muestre que las familias U(X, y) = C, y u(x, y) = c2 son
ortogonales. (b) Trabaje parte (a) pa-ra las funciones F(z) = z.I y F(Z) =
2x’ - iz - 3. (c) iPiensa usted que los resul-tados indicados para estos
casos especiales se cumplen en general? Explique (com-pare con
Ejercicio 4C, página 48).