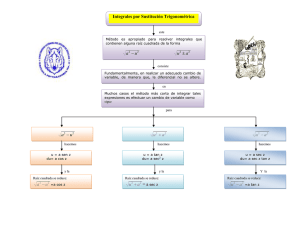
ÍNDICE 1. Métodos de integración 5 1.1. Integrales inmediatas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 1.2. Propiedades de la integral . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 1.3. Integración por sustitución . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 1.4. Integración por partes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 1.5. Integración de funciones Racionales P(x) Q(x) . . . . . . . . . . . . . . . . . . . . 22 1.5.1. El grado de P (x) es mayor o igual que el grado de Q(x). . . . . . . . 22 1.5.2. El grado de P (x) es menor que el grado de Q(x) . . . . . . . . . . . . 24 1.5.3. Cambios que conducen a integrales de fracciones racionales . . . . . . 37 1.6. Integración De Funciones Trigonométricas . . . . . . . . . . . . . . . . . . . Z Z n 1.6.1. Integrales de la forma: sen xdx y cosn xdx. . . . . . . . . . . . . 41 41 1.6.2. Si n es par. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Z 1.6.3. Integrales de la forma: (senm x)(cosn x)dx. . . . . . . . . . . . . . . 43 tann xdx. . . . . . . . . . . . . . . . . . . . 45 1.6.4. Integrales de la forma: Z Z 41 secn xdx. . . . . . . . . . . . . . . . . . 47 1.6.6. Si n es impar. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Z 1.6.7. Integrales de la forma: (tann x)(secm x)dx. . . . . . . . . . . . . . . 47 1.6.5. Integrales de la forma: 1 48 2 Índice R R R 1.6.8. Integrales de la forma: sen(mx) cos(nx)dx, sen(mx)sen(nx)dx, cos(mx) cos(nx)dx. 49 1.7. Integración Por Sustituciones Trigonométricas . . . . . . . . . . . . . . . . . 51 1.8. Integración por sustituciones de Euler . . . . . . . . . . . . . . . . . . . . . . Z 1.9. Integrales de la forma: xm (a + bxn )p dx, con m, n, p ∈ Q . . . . . . . . . . 55 1.9.1. Si p es un número entero. . . . . . . . . . . . . . . . . . . . . . . . . m+1 es un número entero. . . . . . . . . . . . . . . . . . . . . n m+1 + p es un número entero. . . . . . . . . . . . . . . . . . . . 1.9.3. Si n 1.9.2. Si 2. Miscelánea de integrales 56 56 57 57 59 2.1. Ejercicios Propuestos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59 2.2. Solución de los Ejercicios Propuestos . . . . . . . . . . . . . . . . . . . . . . 62 Bibliografía 99 Bibliografía 101 INTRODUCCIÓN El presente trabajo tiene por objetivo hacer una exposición amplia y detallada sobre el cálculo de “funciones primitivas” mediante múltiples ejercicios, enmarcados en la Teoría de Integración, acorde con los programas de Matemáticas 20 y Cálculo 2 de la Facultad de Ciencias, Cálculo 20 en la Facultad de Ingeniería y Matemáticas 2 en la Facultad de Ciencias Forestales y Ambientales; puede ser también utilizado, con los problemas elementales, en otras facultades. La selección del material, para la elaboración de los ejercicios aquí desarrollados, se ha hecho sobre la base del curso de Matemáticas 20 dictado en diferentes oportunidades por la autora de este problemario en las diferentes facultades donde el Departamento de Matemáticas de la Facultad de Ciencias presta su servicio. El enfoque didáctico que se le ha dado permite al estudiante aprender los métodos de integración paso a paso y avanzar gradualmente en la dificultad de los ejercicios. Se sugiere algunos aspectos metodológicos para la resolución, ejercitación y aprendizaje del cálculo integral, que conduce establecer criterios específicos y generales según la exigencia de los programas de las facultades citadas. Para esto, se organizó la presentación del material en dos capítulos, el primero titulado “Métodos de integración”, tiene como objetivo que el estudiante aprenda los métodos con ejercicios elementales, seleccionados a lo largo de los cursos dictados. El segundo capítulo, titulado “Miscelánea”, tiene la intención de que el estudiante, una vez que conozca todos los métodos, se encuentre en capacidad de resolver cualquier ejercicio del cálculo integral. La gran mayoría de estos ejercicios son una recopilación, que a través de los años, se hizo de los diferentes exámenes realizados en la Facultad de Ciencias y en la Facultad de Ingeniería. Una innovación didáctica es que a estos ejercicios propuestos no sólo se les da su respuesta, sino que son resueltos en detalle, recomendando al usuario que intente primero resolverlos y que luego compare la solución; esta experiencia de aprendizaje tiene por finalidad que el estudiante, además de lograr el objetivo cognoscitivo, desarrolle también su capacidad de autoevaluarse. El capítulo 1 se inicia con el cálculo de las primitivas de las funciones básicas: potencias y polinomios, exponenciales generales, funciones trigonométricas y logarítmicas, se sigue con las propiedades lineales de la integración que son consecuencia de aquellas análogas a las 3 4 Índice de la derivación de funciones. Se continua con ejemplos y ejercicios referidos a los métodos de integración, comenzando con el de integración por sustitución, el cual es la expresión de la regla de la cadena en la teoría de derivación. Se sigue con el método de integración por parte, que es la interpretación en la teoría de la integración de la derivada del producto de funciones. Se avanza con las secciones en las que se desarrollan los métodos de integración de funciones racionales y la integración general de funciones trigonométricas, incluyendo potencias y productos de las mismas. Finalmente en este primer capítulo, se trabaja con tres secciones referidas a la integración por sustitución trigonométrica, sustituciones de Euler e integración de funciones binómicas: los productos xm (a + bxn )p , donde m, n, p son números racionales. Esta exposición finaliza con el capítulo 2, Miscelánea de Integrales, del cual ya se hizo referencia. Este material ha sido utilizado en los cursos de Matemáticas 20 dictado por la autora en la Facultad de Ciencias y en la Facultad de Ciencias Forestales y Ambientales y ha tenido una buena aceptación por parte de los estudiantes quienes la consideran como guía práctica y didáctica que les facilita el aprendizaje en este tópico. También ha sido usada como material de referencia por algunos profesores que dictan el curso. CAPÍTULO 1 MÉTODOS DE INTEGRACIÓN La integración es la operación inversa de la derivada. Nuestro objetivo, en la presente guía, es aprender a calcular una integral para después hacer con facilidad sus aplicaciones (Integral definida para calcular áreas, longitudes y volúmenes). R Calcular f (x)dx es encontrar una función g tal que la derivada nos de f , es decir, R f (x)dx = g(x), donde g ′(x) = f (x). En tal caso diremos que g es una antiderivada o primitiva para f Así por ejemplo, ya que [sen(x)]′ = cos(x). Z cos(x)dx = sen(x), Como la derivada de una función constante es cero, entonces podemos sumar cualquier R constante C a la función g, así f (x)dx = g(x) + C. C es llamada constante de integración. Los métodos de Integración son herramientas que nos permiten llevar Integrales no inmediatas a integrales inmediatas. Por eso es importante conocer y visualizar con rapidéz las integrales que son inmediatas. Las fórmulas dadas a continuación nos permiten hacerlo. 1.1. 1. Integrales inmediatas Z xn = xn+1 + C, si n 6= −1. n+1 Ejemplo 1.1.1 5 6 1.1. Integrales inmediatas (i) Z dx = x + C. (ii) Z x3 dx = x4 + C. 4 (iii) Z 1 dx = x7 Z (iv) Z √ 3 2. Z x2 dx = x−7 dx = − Z x2/3 dx = ekx e dx = + C, k kx x−6 1 + C = − 6 + C. 6 6x 3x5/3 x5/3 +C = + C. 5/3 5 Z akx a dx = + C, (a > 0 y a 6= 1). k ln a kx Ejemplo 1.1.2 Z e3x + C. (i) e3x dx = 3 2x + C. ln 2 (ii) Z 2x dx = (iii) Z 52x dx = 52x + C. 2 ln 5 (iv) Z 1 dx = e5x Z 3. Z e−5x dx = − sen(kx)dx = − e−5x + C. 5 sen(kx) + C. k Ejemplo 1.1.3 Z cos(2x) (i) sen(2x)dx = − + C. 2 (ii) Z sen cos 31 x 1 1 x dx = − x + C. + C = −3 cos 1 3 3 3 7 1. Métodos de integración 4. Z cos(kx)dx = sen(kx) + C. k Ejemplo 1.1.4 Z sen(7x) + C. (i) cos(7x)dx = 7 (ii) Z sen 51 x 1 1 + C = 5sen cos x dx = x + C. 1 5 5 5 (iii) Z cos(−4x)dx = 5. Z −sen(4x) sen(4x) sen(−4x) +C = +C = + C. −4 −4 4 f ′ (x) dx = ln |f(x)| + C. f(x) Observación 1.1.1 Aplicamos esta fórmula en el caso de tener un cociente donde el numerador es la derivada del denominador. Ejemplo 1.1.5 Z 1 (i) dx = ln |x| + C. x (ii) Z 1 dx = ln |x + 2| + C. x+2 (iii) Z x 1 dx = 2 x +3 2 (iv) Z e−x dx = − e−x + 1 (v) Z 1 + ln x dx = ln |3 + x ln x| + C. 3 + x ln x (vi) Z tan xdx = Z 2x 1 dx = ln |x2 + 3| + C. +3 2 Z x2 Z −e−x dx = − ln |e−x + 1| + C. −x e +1 senx dx = − cos x Z −senx dx = − ln | cos x| + C. cos x 8 1.1. Integrales inmediatas (vii) Z cot xdx = Z (viii) Z cos x dx = ln |senx| + C. senx (sec x)(sec x + tan x) dx = sec x + tan x Z sec xdx = Z sec2 x + sec x tan x dx sec x tan x = ln | sec x + tan x| + C. Z (ix) csc xdx = − Z −(csc x)(csc x + cot x) dx = − csc x + cot x Z − csc2 x − csc x cot x dx csc x + cot x = − ln | csc x + cot x| + C. 6. Z [f(x)]n+1 + C, n+1 [f(x)]n f ′ (x)dx = si n 6= −1. Ejemplo 1.1.6 Z sen4 x (i) sen3 x cos x = + C. 4 tan3 x + C. 3 (ii) Z tan2 x sec2 x = (iii) Z arcsenx √ dx = 1 − x2 (iv) Z dx = 5 (arctan x)(1 + x2 ) (v) Z 1 ln3 x dx = 3x 3 (vi) Z (ln x + 2)2 dx = x 7. Z Z Z arcsenx √ Z (arctan−5 x) 1 arctan−4 x dx = − + C. 1 + x2 4 1 1 ln4 x ln4 x ln x dx = +C = + C. x 3 4 12 3 Z (ln x + 2)3 1 (ln x + 2)2 dx = + C. x 3 ef (x) f ′ (x)dx = ef (x) + C. Ejemplo 1.1.7 1 arcsen2 x dx = + C. 2 1 − x2 9 1. Métodos de integración 1 2 2 ex 2xdx = ex + C. 2 (i) Z 1 e xdx = 2 (ii) Z esenx (cos x)dx = esenx + C. (iii) Z e x √ dx = 2 x (iv) Z x2 dx = ex3 1.2. 1. x2 √ Z Z Z √ e √ 1 √ dx = 2e x + C. 2 x x 1 x dx = − 3 −x3 2 e 1 3 3 e−x (−3x2 )dx = − e−x + C. 3 Z Propiedades de la integral Z [f(x) ± g(x)]dx = Z f(x)dx ± Z g(x)dx. Ejemplo 1.2.1 Z Z Z 1 cos(4x) e2x sen(4x) + 2x dx = sen(4x)dx + e−2x dx = − − + C. e 4 2 2. Z c · f(x)dx = c Z f(x)dx, ∀ c ∈ R. Ejemplo 1.2.2 Z Z (i) 2 cos(8x)dx = 2 cos(8x)dx = 2 sen(8x) +C 8 sen(8x) + C. 4 Z Z 2 3 (ii) (x + 5) dx = (x6 + 15x4 + 75x2 + 125)dx = = = Z 6 x dx + 15 Z 4 x dx + 75 Z 2 x dx + 125 x7 + 3x5 + 25x3 + 125x + C. 7 Z dx 10 1.3. Integración por sustitución (iii) Z ln2 x + 2x2 dx = x Z 1 ln x dx + 2 x 2 Z x2 dx = x Z 1 ln x dx + 2 x 2 Z xdx x2 ln3 x ln3 x +2 +C = + x2 + C. = 3 2 3 Z 2x Z 2x Z Z Z e +3 e 1 −2x (iv) dx = dx + 3 dx = e dx + 3 e−4x dx e4x e4x e4x 1 3 = − e−2x − e−4x + C. 2 4 Z Z dx 1 (v) dx = dx 2 2 2 sen x cos x sen x cos2 x Z sen2 x + cos2 x = dx sen2 x cos2 x Z Z sen2 x cos2 x = dx + dx sen2 x cos2 x sen2 x cos2 x Z Z 1 1 dx + dx = cos2 x sen2 x Z Z 2 = sec xdx + csc2 dx = tan x − cot x + C. (vi) 1.3. Z 2 tan xdx = Z 2 (sec x − 1)dx = Z 2 sec xdx − Z dx = tan x − x + C. Integración por sustitución El método de sustitución o cambio de variable consiste, como su nombre lo indica, en cambiar una función diferenciable g(x) por una nueva variable t, de tal manera que este cambio nos lleve a una integral inmediata. En algunas fórmulas que dimos como integrales inmediatas podemos hacer una sustitución; sin embargo, la idea de darlas como fórmulas es para resolverlas rápidamente y para crear facilidad en visualizarlas. R Sea f (g(x)) · g ′(x)dx, y llamemos g(x) = t. Así, g ′(x)dx = dt y la integral nos queda: Z Z ′ f (g(x)) · g (x)dx = f (t)dt. En efecto, si F es una antiderivada de f entonces Z Z Z ′ ′ ′ f (g(x))g (x)dx = F (g(x))g (x)dx = (F ◦ g)′(x)dx = (F ◦ g)(x) + C 11 1. Métodos de integración Ejemplo 1.3.1 (i) Z ln3 x dx = x 1 (ln3 x) dx. x Z Llamemos t = ln x, de donde obtenemos dt = Z (ii) Z √ 3 ln3 x dx = x Z 1 (ln x) dx = x 3 Z 1 dx. Así: x t4 ln4 x t dt = + C = + C. 4 4 3 1 + 3senx cos xdx. Llamemos t = 1 + 3senx, de donde obtenemos dt = 3 cos xdx. De esta manera: Z √ 3 1 cos x 1 + 3senxdx = 3 Z 1 = 3 Z (iii) √ 1 1 + 3senx 3 cos xdx = 3 t1/3 dt = 1 t4/3 +C · 3 43 Z √ 3 tdt 1 (1 + 3senx)4/3 + C. 4 = Z √ 3 x dx. x2 + 5 Llamemos t = x2 + 5, de donde obtenemos dt = 2xdx. Luego: Z (iv) Z Z Z Z 1 t1/2 2xdx dt 1 1 1 x √ √ √ = t−1/2 dt = · 1 + C = = 2 2 2 2 2 t x2 + 5 x2 + 5 √ √ t + C = x2 + 5 + C. = e3 cos x senxdx. Llamemos t = cos x, de donde obtenemos dt = −senxdx, así Z 3 cos x e senxdx = − Z e3t dt = − e3 cos x e3t +C =− + C. 3 3 12 (v) 1.3. Integración por sustitución Z cos(senx) cos xdx. Llamemos t = senx, de donde obtenemos dt = cos xdx, así Z (vi) Z Z cos(senx) cos xdx = cos tdt = sent + C = sen(senx) + C. √ x x − 5dx. Consideremos t = x − 5. Así, x = t + 5 y dx = dt. De esta forma tenemos que Z √ x x − 5dx = Z = Z √ (t + 5) tdt = √ 3 √ Z √ √ (t t + 5 t)dt = [( t) + 5 t]dt = Z √ 3 ( t) dt + Z Z √ 3 ( t) dt + Z √ 5 tdt √ 5 tdt Z √ Z √ 2 √ 10 √ 3 = ( t) dt + 5 tdt = ( t)5 + ( t)3 + C. 5 3 10 √ 2 √ = ( x − 5)5 + ( x − 5)3 + C. 5 3 Otra forma: tomemos t2 = x − 5, de donde x = t2 + 5 y de aquí obtenemos dx = 2tdt, así Z √ x x − 5dx = Z =2 Z Z Z √ 2 2 4 2 (t + 5) t 2tdt = 2 (t + 5)t dt = 2 t dt + 2 5t2 dt 2 Z 4 t dt + 10 Z 2 10 t2 dt = t5 + t3 + C 5 3 10 √ 2 √ = ( x − 5)5 + ( x − 5)3 + C. 5 3 (vii) Z (2x + 1)20 dx. Llamemos t = 2x + 1, de donde obtenemos dt = 2dx, así 13 1. Métodos de integración Z (viii) Z 1 (2x + 1) dx = 2 20 (2 ln x + 3)3 dx = x Z 1 (2x + 1) 2dx = 2 Z 20 Z t20 dt = 1 t21 (2x + 1)21 +C = + C. 2 21 42 1 (2 ln x + 3)3 dx. x 1 Llamemos t = 2 ln x + 3, de donde obtenemos dt = 2 dx, así x Z Z Z 1 t4 1 1 3 1 31 (2 ln x + 3) 2 dx = t3 dt = +C (2 ln x + 3) dx = x 2 x 2 24 1 1 = t4 + C = (2 ln x + 3)4 + C. 8 8 (ix) Z r arcsenx dx = 1 − x2 Z (arcsenx)1/2 √ 1 dx. 1 − x2 Llamemos t = arcsenx, de donde obtenemos dt = √ Z (x) Z (arcsenx) 1/2 1 √ dx = 1 − x2 Z t1/2 dt = t3/2 3 2 1 dx, así 1 − x2 2 + C = (arcsenx)3/2 + C. 3 √ sen x √ dx. x √ 1 x, de donde obtenemos dt = √ dx, así 2 x √ √ Z Z Z Z √ 1 sen x sen x √ dx = 2 sen x √ dx = 2 sentdt √ dx = 2 x 2 x 2 x Llamemos t = √ = −2 cos t + C = −2 cos x + C. (xi) Z x3 dx √ dx. 5 x4 + 6 Llamemos t = x4 + 6, de donde obtenemos dt = 4x3 dx, así Z 1 x3 dx √ dx = 5 4 x4 + 6 = Z 1 4x3 dx √ dx = 5 4 x4 + 6 Z dt 1 √ = 5 4 t 1p 1√ 5 t4 + C = 5 (x4 + 6)4 + C. 4 4 Z 1 t−1/5 dt = t4/5 + C 4 14 1.4. Integración por partes (xii) √ x2 1 + xdx. Z Llamemos 1 + x = t2 , de donde x = t2 − 1 y de aquí obtenemos dx = 2tdt, así Z 2 x √ 1 + xdx = 2 Z 2 2 2 (t − 1) t dt = 2 Z (t4 − 2t2 + 1)t2 dt = t7 t5 t3 −2 + +C 7 5 3 p p p (1 + x)7 (1 + x)5 (1 + x)3 −2 + + C. = 7 5 3 1.4. Integración por partes Si en la integral Z f (x) g(x) dx llamamos u = f (x) y dv = g(x)dx, tenemos que Z f (x) g(x) dx = Z u dv. Al derivar u =R f (x), obtenemos que du = f ′ (x) dx. Por otro lado, al integrar dv = g(x) dx se tiene que v = g(x) dx = G(x), es decir, G′ (x) = g(x). De esta manera Z Z Z ′ f (x) g(x) dx = f (x) G (x) dx = u dv Nuestro propósito es calcular esta integral. Derivemos el producto f (x) G(x). Así [f (x) G(x)]′ = f ′ (x) G(x) + f (x) G′ (x) De esta manera integrando en ambos miembros de la igualdad obtenemos Z Z ′ f (x) G(x) + C = f (x) G(x) dx + f (x) G′ (x) dx. Podemos suprimir la constante C ya que el cálculo de las integrales originarán constantes. Así: Z Z ′ f (x) G (x) dx = f (x) G(x) − G(x) f ′ (x) dx, es decir, Z u dv = u v − Z v du. Esta ecuación es conocido como la fórmula de integración por partes. 15 1. Métodos de integración Ejemplo 1.4.1 (i) Z xex dx. Tomemos u = x −→ du =Zdx dv = ex dx −→ v = ex dx = ex . Así (ii) Z Z x xe dx = uv − Z x vdu = xe − Z ex dx = xex − ex + C. x2 senxdx. Tomemos u = x2 −→ du =Z2xdx dv = senxdx −→ v = senxdx = − cos x. Así, Z 2 2 x senxdx = −x cos x + Z 2 cos(x)2xdx = −x cos x + 2 Aplicamos nuevamente integración por partes a Z Z x cos xdx. x cos xdx. u = x −→ du =Zdx dv = cos xdx −→ v = cos xdx = senx. Sustituyendo en la ecuación anterior tenemos Z Z 2 2 x senxdx = −x cos x + 2 xsenx − senxdx = −x2 cos x + 2xsenx + 2 cos x + C. A pesar de que en algunos casos es indiferente llamar u a cualquier función, lo más recomendable al aplicar este método es seguir un criterio que nos da la prioridad para elegir la función que conviene llamarse u. La prioridad para u es: Logarítmicas, Inversas (arcos, radicales), Polinómicas, Trigonométricas y Exponenciales. (iii) Z x3 ln xdx. Aquí tenemos un producto de una función Polinómica y una Logarítmica, entonces la prioridad para u es la función Logarítmica. 16 1.4. Integración por partes Tomemos 1 dx x4 x dv = x3 dx −→ v = . 4 u = ln x −→ du = Así Z (iv) Z x4 ln x − x ln xdx = 4 3 x4 1 x4 1 dx = ln x − 4 x 4 4 Z Z x3 dx = x4 x4 ln x − + C. 4 16 ln xdx. Tomemos 1 dx x dv = dx −→ v = x, Z Z Z 1 ln xdx = x ln x − x dx = x ln x − dx = x ln x − x + C. x u = ln x −→ du = (v) Z arctan xdx. Tomemos 1 dx 1 + x2 v = x. u = arctan x −→ du = dv = dx −→ Así Z arctan xdx = x arctan x − = x arctan x − (vi) Z Z 1 1 dx = x arctan x − x 2 1+x 2 Z 2x dx 1 + x2 1 ln(1 + x2 ) + C. 2 arcsenxdx. Tomemos 1 dx 1 − x2 v = x. u = arcsenx −→ du = √ Así Z dv = dx −→ arcsenxdx = xarcsenx − = xarcsenx − Z 1 1 dx = xarcsenx − x√ 2 1 − x2 Z (1 − x2 )−1/2 2xdx √ 1 (1 − x2 )1/2 · + C = xarcsenx − 1 − x2 + C. 1 2 2 17 1. Métodos de integración (vii) Z (x2 − 2x + 5)e−x dx. Tomemos Así u = x2 − 2x + 5 −→ du = (2x − 2)dx dv = e−x dx −→ v = −e−x . Z 2 2 −x )+ Z e−x (2x − 2)dx +2 Z e−x (x − 1)dx. −x (x − 2x + 5)e dx = (x − 2x + 5)(−e 2 −x = −(x − 2x + 5)e Z Aplicamos nuevamente integración por partes a e−x (x − 1)dx. u = x − 1 −→ du = dx dv = e−x dx −→ v = −e−x . Z 2 2 −x −x (x − 2x + 5)e dx = −(x − 2x + 5)e Z −x −x + 2 (x − 1)(−e ) + e dx = −(x2 − 2x + 5)e−x − 2(x − 1)e−x − 2e−x + C. Simplificando la expresión tenemos finalmente: Z (x2 − 2x + 5)e−x dx = −e−x (x2 + 5) + C. (viii) Z ex cos xdx. Tomemos Así u = cos x −→ du = −senxdx dv = ex dx −→ v = ex . Z x x e cos xdx = e cos x − Z x x e (−senx)dx = e cos x + Aplicamos nuevamente integración por partes a Z Z ex senxdx ex senxdx. u = senx −→ du = cos xdx dv = ex dx −→ v = ex . Sustituyendo en la ecuación anterior tenemos Z Z x x x x e cos xdx = e cos x + e senx − e cos x dx. 18 1.4. Integración por partes Observemos que después de aplicar el método llegamos a la integral inicial, entonces tratamos la expresión como una ecuación. 2 Z Z (ix) Z ex cos xdx = ex cos x + ex senx + C. ex cos xdx = ex (cos x + senx) + C. 2 e5x sen(4x)dx. Tomemos Así Z u = sen(4x) −→ du = 4 cos(4x)dx e5x 5x dv = e dx −→ v = . 5 e5x e sen(4x)dx = sen(4x) − 5 5x Z e5x 4 e5x 4 cos(4x)dx = sen(4x) − 5 5 5 Aplicamos nuevamente integración por partes a Z Z e5x cos(4x)dx. e5x cos(4x)dx. u = cos(4x) −→ du = −4sen(4x)dx e5x 5x . dv = e dx −→ v = 5 Sustituyendo en la ecuación anterior tenemos Z 5x Z 4 e5x e e5x 5x sen(4x) − cos(4x) − (−4sen(4x)) dx e sen(4x)dx = 5 5 5 5 e5x 4 16 = sen(4x) − e5x cos(4x) − 5 25 25 Z e5x sen(4x)dx. Observemos que después de aplicar el método llegamos a la integral inicial, entonces tratamos la expresión como una ecuación. Z 16 e sen(4x)dx + 25 5x 41 25 Z 1 4 e5x sen(4x)dx = e5x sen(4x) − e5x cos(4x) + C. 5 25 Z 4 1 5x e sen(4x)dx = e sen(4x) − cos(4x) + C. 5 5 Z 5e5x [sen(4x) − 45 cos(4x)] e sen(4x)dx = + C. 41 5x 5x 19 1. Métodos de integración (x) Z cos(ln x)dx. Tomemos u = cos(ln x) −→ du = − Así Z dv = dx −→ v = x, cos(ln x)dx = x cos(ln x) − Z sen(ln x) dx x 1 x[−sen(ln x)] dx = x cos(ln x) + x Aplicamos nuevamente integración por partes a Z Z sen(ln x)dx. sen(ln x)dx. 1 u = sen(ln x) −→ du = cos(ln x) dx x dv = dx −→ v = x. Sustituyendo en la ecuación anterior tenemos Z Z 1 cos(ln x)dx = x cos(ln x) + xsen(ln x) − x cos(ln x) dx x Z = x cos(ln x) + xsen(ln x) − cos(ln x)dx. Observemos que después de aplicar el método llegamos a la integral inicial, entonces tratamos la expresión como una ecuación. Z 2 cos(ln x)dx = x cos(ln x) + xsen(ln x) + C. Z x[cos(ln x) + sen(ln x)] cos(ln x)dx = + C. 2 (xi) Z (senx) ln(tan x)dx. Tomemos 1 dx senx cos x dv = senxdx −→ v = − cos x. u = ln(tan x) −→ du = Así Z (senx) ln(tan x)dx = −(cos x) ln(tan x) − = −(cos x) ln(tan x) − Z Z cos x 1 dx senx cos x csc xdx = −(cos x) ln(tan x) − ln | csc x + cot x| + C. 20 (xii) 1.4. Integración por partes Z √ √ ln( 1 − x + 1 + x)dx. Tomemos √ √ u = ln( 1 − x + 1 + x) −→ du= √ 1 = 2 √ 1 1 1 √ − √ dx + √ 2 1−x 2 1+x 1−x+ 1+x 1 − x2 − 1 √ dx. 1 − x2 dv = dx −→ v = x. Así Z √ ln( 1 − x + √ √ x 1 − x2 − 1 √ dx 1 + x)dx = x ln( 1 − x + x 1 − x2 Z Z √ √ 1 1 dx √ dx + = x ln( 1 − x + 1 + x) − 2 2 1 − x2 √ √ 1 1 + x) − 2 Z √ √ 1 1 = x ln( 1 − x + 1 + x) − x + arcsenx + C. 2 2 (xiii) Z ln(x + √ 1 + x2 )dx. Tomemos u = ln(x + √ 1+ x2 ) 1 √ −→ du= x + 1 + x2 1 √ x + 1 + x2 dx =√ . 1 + x2 = 2x 1+ √ dx 2 1 + x2 ! √ 1 + x2 + x √ dx 1 + x2 dv = dx −→ v = x Z ln(x + √ 1+ x2 )dx = x ln(x + √ = x ln(x + √ √ Z 1+ x2 ) − 1+ x2 ) 1 − 2 x√ Z dx dx 1 + x2 1 (1 + x2 )− 2 2xdx 1 1 (1 + x2 ) 2 +C − = x ln(x + 1 + 1 2 2 √ √ = x ln(x + 1 + x2 ) − 1 + x2 + C. x2 ) 21 1. Métodos de integración (xiv) Z 2x3 sen(x2 )dx. Antes de aplicar el método escribamos de manera conveniente. Z Z Z 3 2 2 2 2x sen(x )dx = 2xx sen(x )dx = x2 sen(x2 )2xdx. Hacemos un cambio de variable. Llamemos t = x2 , de donde obtenemos dt = 2xdx, así Z Z Z 3 2 2 2 2x sen(x )dx = x sen(x )2xdx = tsentdt. Por ultimo aplicamos integración por partes a Z tsentdt. Tomemos u = t −→ du = dt dv = sentdt −→ v = − cos t. Así Z 3 2 2x sen(x )dx = Z tsentdt = −t cos t + Z cos tdt = −t cos t + sent + C = −x2 cos(x2 ) + sen(x2 ) + C. (xv) Z 3 x5 e−x dx Antes de aplicar el método, es conveniente reescribirla como remos el siguiente cambio de variable: Z 3 x3 e−x x2 dx, y conside- t = x3 −→ dt = d3x2 dx Así Z 1 te−t dt x e dx = 3 Z Aplicamos así integración por partes a te−t dt. Tomemos Z 5 −x3 u = t −→ du = dt dv = e−t dt −→ v = −e−t Así Z 1 x dx = 3 3 −x3 2 xe Z 1 te dt = 3 −t Z 1 1 −t −te + e−tdt = − te−t − e−t + C 3 3 1 1 3 3 = − x3 e−x − e−x + C 3 3 22 1.5. Integración de funciones Racionales P(x) Q(x) R m Observación 1.4.1 Éstas dos últimas integrales ((xiv), (xv)) son de la forma x sen(xn )dx R m xn m n n−1 y x e dx, donde m = 2n − 1. En este caso se escribe x como x x y se integra por partes. 1.5. Integración de funciones Racionales P(x) Q(x) En esta sección nos dedicaremos a integrar funciones de la forma un polinomio de grado m y Q(x) es un polinomio de grado n. P (x) , donde P (x) es Q(x) El grado de P (x) es mayor o igual que el grado de Q(x). 1.5.1. Si m ≥ n hacemos la división de polinomios. Recordemos además que al hacer la división P (x) entre Q(x) se tiene que P (x) R(x) = C(x) + , Q(x) Q(x) donde C(x) y R(x) son los polinomios cociente y resto resultantes de dicha división, respectivamente. Ejemplo 1.5.1 (i) Z x dx. x+1 Observemos que GradoP (x) = GradoQ(x) = 1. Al dividir se tiene que Así Z (ii) Z x dx = x+1 Z x 1 = 1− . x+1 1+x Z Z 1 1 dx = dx − 1− dx = x − ln |x + 1| + C. 1+x 1+x x2 dx. x2 + 1 Similar al ejemplo anterior, GradoP (x) = GradoQ(x) = 2, obteniéndose al dividir que x2 1 =1− 2 . De esta forma 2 x +1 x +1 Z Z Z Z 1 1 x2 dx = dx − dx = 1− 2 dx = x − arctan x + C. 2 2 x +1 x +1 x +1 (iii) Z x3 + 1 dx. x−2 23 1. Métodos de integración Observemos que GradoP (x) > GradoQ(x), pero Z x3 + 1 dx = x−2 9 dx (x + 2x + 4) + x−2 Z Z Z Z 2 = x dx + 2 xdx + 4 dx + 9 Z (iv) 2 1 dx x−2 x3 + x2 + 4x + 9 ln |x − 2| + C. 3 = Z 9 x3 + 1 = (x2 + 2x + 4) + . Así x−2 x−2 1 x ln 1 + dx. x Integramos primero por partes. Para ello tomemos 1 −1 − 2 dx = −→ du = dx 1 x (x + 1)x 1+ x 2 x dv = xdx −→ v = 2 1 u = ln 1 + x Así Z 1 Z 2 x2 1 x 1 1 dx = − − dx ln 1 + x ln 1 + x 2 x 2 x(x + 1) Z x2 1 x2 1 = + ln 1 + dx 2 x 2 x(x + 1) Z x2 1 x 1 = + ln 1 + dx. 2 x 2 x+1 En la integral Z Z x dx hacemos la división y obtenemos: x+1 x dx = x+1 Z 1 1− x+1 dx = Z dx − Z 1 dx = x + ln |x + 1| + C. x+1 Sustituyendo en la ecuación anterior tenemos: Z 1 x ln 1 + x x2 1 1 dx = + (x − ln |x + 1| ) + C. ln 1 + 2 x 2 24 1.5. Integración de funciones Racionales P(x) Q(x) El grado de P (x) es menor que el grado de Q(x) 1.5.2. Si m < n se usa el método de los coeficientes indeterminados o suma de fracciones simples el cual presenta cuatro casos. 1.5.2.1. Caso 1: Cuando Q(x) se puede factorizar como el producto de factores lineales todos distintos (raíces reales distintas), es decir; cuando Q(x) = (x − a)(x − b) . . . (x − l), donde a, b, . . . , l son todas raíces reales y distintas del polinomio Q(x). Observación 1.5.1 Por factor lineal entendemos factores de grado 1. Ejemplo 1.5.2 (i) x+1 dx. x2 − 4 Observemos que Q(x) = x2 − 4 = (x − 2)(x + 2) (factores lineales distintos). Z x+1 x+1 A B A(x + 2) + B(x − 2) = = + = . 2 x −4 (x − 2)(x + 2) x−2 x+2 (x − 2)(x + 2) Igualando los numeradores tenemos: (1.1) x + 1 = A(x + 2) + B(x − 2) Damos valores a x que anulen los denominadores y los sustituimos en (1.1). 1 Para x = −2 obtenemos −1 = B(−4), y de aquí B = . 4 3 Para x = 2 obtenemos 3 = A(4), y de aquí A = . 4 Así: Z x+1 dx = x2 − 4 = (ii) Z 15x2 − 4x − 81 dx. x3 − 13x + 12 Z A dx + x−2 Z B 3 dx = x+2 4 3 1 ln |x − 2| + ln |x + 2| + C. 4 4 Z 1 1 dx + x−2 4 Z 1 dx x+2 25 1. Métodos de integración Observemos que Q(x) = x3 −13x+12 = (x−3)(x+4)(x−1) (factores lineales distintos). 15x2 − 4x − 81 15x2 − 4x − 81 A B D = = + + 3 x − 13x + 12 (x − 3)(x + 4)(x − 1) x−3 x+4 x−1 = A(x + 4)(x − 1) + B(x + 3)(x − 1) + D(x − 3)(x + 4) . (x − 3)(x + 4)(x − 1) Igualando los numeradores tenemos: 15x2 − 4x − 81 = A(x + 4)(x − 1) + B(x − 3)(x − 1) + D(x − 3)(x + 4) (1.2) Damos valores a x que anulen los denominadores y los sustituimos en (1.2). Para x = 3 obtenemos 135 − 12 − 81 = A(7)(2), y de aquí A = 3. Para x = −4 obtenemos 240 + 16 − 81 = B(−7)(−5), y de aquí B = 5. Para x = 1 obtenemos 15 − 4 − 81 = D(−2)(5), y de aquí D = 7. Así Z 15x2 − 4x − 81 dx = A x3 − 13x + 12 Z 1 dx + B x−3 Z 1 dx + D x+4 Z 1 dx x−1 = 3 ln |x − 3| + 5 ln |x + 4| + 7 ln |x − 1| + C. (iii) x4 − 3x2 − 3x − 2 dx. x3 − x2 − 2x Observemos que Grado P (x) > Grado Q(x), pero Z Así x+2 x4 − 3x2 − 3x − 2 =x+1− , 3 2 2 x − x − 2x x(x − x − 2) Z x4 − 3x2 − 3x − 2 dx = x3 − x2 − 2x Z (x + 1)dx − Z x+2 dx. − x − 2) x(x2 x+2 dx aplicamos el método de fracciones simples. Obserx(x2 − x − 2) vemos que Q(x) = x(x2 − x − 2) = x(x − 2)(x + 1) (factores lineales distintos). Para la integral Z x+2 A B D x+2 = = + + x(x2 − x − 2) x(x − 2)(x + 1) x x−2 x+1 = A(x − 2)(x + 1) + Bx(x + 1) + Dx(x − 2) . x(x − 2)(x + 1) 26 1.5. Integración de funciones Racionales P(x) Q(x) Igualando los numeradores tenemos: x + 2 = A(x − 2)(x + 1) + Bx(x + 1) + Dx(x − 2) (1.3) Damos valores a x que anulen los denominadores y los sustituimos en (1.3). Para x = 0 obtenemos 2 = A(−2)(1), y de aquí A = −1. 2 Para x = 2 obtenemos 4 = B(2)(3), y de aquí B = . 3 Para x = −1 obtenemos 1 = D(−1)(−3), y de aquí D = 1 3 Así Z x4 − 3x2 − 3x − 2 dx = x3 − x2 − 2x (x + 1)dx − Z x+2 dx − x − 2) x(x2 Z A B D = (x + 1)dx − dx + + x x−2 x+1 Z Z Z Z dx dx 1 dx 2 − − = (x + 1)dx + x 3 x−2 3 x+1 Z Z Z Z Z dx 2 dx dx 1 = xdx + dx + − − x 3 x−2 3 x+1 = 1.5.2.2. Z Z x2 2 1 + x + ln |x| − ln |x − 2| − ln |x + 1| + C. 2 3 3 Caso 2: Cuando Q(x) se puede factorizar como el producto de factores lineales no todos distintos (raíces reales repetidas). Ejemplo 1.5.3 (i) 2x2 − 3x + 3 dx. x3 − 2x2 + x Observemos que Z Q(x) = x3 − 2x2 + x = x(x2 − 2x + 1) = x(x − 1)(x − 1) = x(x − 1)2 . De esta manera tenemos que 2x2 − 3x + 3 2x2 − 3x + 3 = x3 − 2x2 + x x(x − 1)2 = = A B D + + x x − 1 (x − 1)2 A(x − 1)2 + Bx(x − 1) + Dx . x(x − 1)2 27 1. Métodos de integración Igualando los numeradores tenemos: 2x2 − 3x + 3 = A(x − 1)2 + Bx(x − 1) + Dx (1.4) Damos valores a x que anulen los denominadores y los sustituimos en (1.4). Para x = 0 obtenemos 3 = A(1), y de aquí A = 3. Para x = 1 obtenemos 2 = D(1), y de aquí D = 2. Damos ahora a x un valor arbitrario y lo sustituimos en (1.4). Para x = −1 obtenemos 8 = A(4) + B(−1)(−2) + D(−1), y de aquí B = −1, así Z 2x2 − 3x + 3 dx = x3 − 2x2 + x Z A B D + + dx x x − 1 (x − 1)2 Z Z Z dx dx dx = A +B +D x x−1 (x − 1)2 Z Z Z dx dx dx = 3 − +2 x x−1 (x − 1)2 Z Z Z dx dx − + 2 (x − 1)−2 dx = 3 x x−1 = 3 ln |x| − ln |x − 1| + = 3 ln |x| − ln |x − 1| − (ii) Z x3 + 1 dx. (x + 2)(x − 1)3 2(x − 1)−1 +C −1 2 + C. x−1 Observemos que Q(x) = (x + 2)(x − 1)3 . A B D E x3 + 1 = + + + 3 2 (x + 2)(x − 1) x + 2 x − 1 (x − 1) (x − 1)3 A(x − 1)3 + B(x + 2)(x − 1)2 + D(x + 2)(x − 1) + E(x + 2) . (x + 2)(x − 1)3 Igualando los numeradores tenemos: = x3 + 1 = A(x − 1)3 + B(x + 2)(x − 1)2 + D(x + 2)(x − 1) + E(x + 2) Damos valores a x que anulen los denominadores y los sustituimos en (1.5). Para x = −2 obtenemos −7 = A(−27), y de aquí A = 7 . 27 (1.5) 28 1.5. Integración de funciones Racionales P(x) Q(x) 2 Para x = 1 obtenemos 2 = E(3), y de aquí E = . 3 Damos ahora a x un valor arbitrario y lo sustituimos en (1.5). Para x = 0 obtenemos 1 = A(−1) + B(2)(1) + D(2)(−1) + E(2), y de aquí B−D =− 1 27 (1.6) Para x = −1 obtenemos 0 = A(−8) + B(1)(4) + D(1)(−2) + E(1), y de aquí 2B − D = 19 27 (1.7) Calculado la diferencia, término a término, de las ecuaciones (1.7) menos (1.6) tenemos 20 20 7 que B = , de donde B = y por último D = . Así 27 27 9 Z Z Z Z Z x3 + 1 dx dx dx dx = A +B +D +E 3 2 (x + 2)(x − 1) x+2 x−1 (x − 1) (x − 1)3 = (iii) 20 7 1 7 ln |x + 2| + ln |x − 1| − − + C. 27 27 9(x − 1) 3(x − 1)2 x4 − 6x3 + 12x2 + 6 dx. x3 − 6x2 + 12x − 8 Observemos que Grado P (x) > Grado Q(x), pero Z x4 − 6x3 + 12x2 + 6 8x + 6 =x+ 3 . 3 2 x − 6x + 12x − 8 x − 6x2 + 12x − 8 Así Z Z Z 4 8x + 6 x − 6x3 + 12x2 + 6 dx = xdx + dx. x3 − 6x2 + 12x − 8 x3 − 6x2 + 12x − 8 Z 8x + 6 Para la integral dx aplicamos el método de fracciones simples. x3 − 6x2 + 12x − 8 Observemos que Q(x) = x3 − 6x2 + 12x − 8 = (x − 2)3 . x3 8x + 6 A B D 8x + 6 = = + + 2 3 2 − 6x + 12x − 8 (x − 2) x − 2 (x − 2) (x − 2)3 A(x − 2)2 + B(x − 2) + D = . (x − 2)3 Igualando los numeradores tenemos: 8x + 6 = A(x − 2)2 + B(x − 2) + D Damos valores a x que anulen los denominadores y los sustituimos en (1.8). (1.8) 29 1. Métodos de integración Para x = 2 obtenemos 22 = D Damos ahora a x un valor arbitrario y lo sustituimos en (1.8). Para x = 0 obtenemos 6 = A(4) + B(−2)(1) + D, y de aquí (1.9) − 8 = 2A − B Para x = 1 obtenemos 14 = A(1) + B(−1) + D, y de aquí (1.10) −8=A−B Haciendo la diferencia de (1.9) menos (1.10) tenemos A = 0, y por lo tanto B = 8. Así Z x4 − 6x3 + 12x2 + 6 dx = x3 − 6x2 + 12x − 8 Z dx dx xdx + A +D 2 (x − 2) (x − 2)3 Z Z Z −2 = xdx + 8 (x − 2) dx + 22 (x − 2)−3 dx = Z Z dx +B x−2 Z x2 8 11 − − + C. 2 x − 2 (x − 2)2 Observación 1.5.2 En algunos casos, para calcular integrales de funciones racionales es conveniente hacer un cambio de variable para simplificar el cálculo de la integral. Ejemplo 1.5.4 Z x2 dx. (x − 1)5 Llamemos x − 1 = t, de donde x = t + 1y de aquí obtenemos dx = dt, así Z x2 dx = (x − 1)5 Z 2 Z Z (t + 1)2 t + 2t + 1 1 dt = dt = dt + 2 t5 t5 t3 Z Z Z 2 1 −3 −4 = t dt + 2 t dt + t−5 dt = − 2 − 3 − 2t 3t Z = − 1 2 1 − − + C. 2 3 2(x − 1) 3(x − 1) 4(x − 1)4 1 dt + t4 1 +C 4t4 Z 1 dt t5 30 1.5. Integración de funciones Racionales 1.5.2.3. P(x) Q(x) Caso 3: Cuando Q(x) se factoriza como producto de factores cuadráticos distintos. Observación 1.5.3 Entendemos por factor cuadrático un polinomio irreducible de grado mayor que 1 (polinomios que no tengan raíces reales) como: x2 + 1 P (x) = 2 . Q(x) x +x+5 En el caso de la descomposición en suma de fracciones simples, en la fracción cuyo denominador sea cuadrático, su numerador es un polinomio completo de grado 1, es decir; un polinomio Ax + B, con A y B números reales. Ejemplo 1.5.5 (i) x+2 dx. x3 + x Observemos que Q(x) = x3 + x = x(x2 + 1). Z x+2 A Bx + D A(x2 + 1) + (Bx + D)x x+2 = = + = . x3 + x x(x2 + 1) x x2 + 1 x(x2 + 1) Igualando los numeradores tenemos: x + 2 = A(x2 + 1) + (Bx + D)x (1.11) Damos valores a x que anulen los denominadores y los sustituimos en (1.11). Para x = 0 obtenemos 2 = A(1), y de aquí A = 2. Damos ahora a x un valor arbitrario, distinto al anterior, y lo sustituimos en (1.11). Para x = 1 obtenemos 3 = A(2) + (B(1) + D)(1), y de aquí −1 =B+D (1.12) Parax = −1 obtenemos 1 = A(2) + (B(−1) + D)(−1), y de aquí −3 =B−D (1.13) Sumando (1.12) y (1.13) tenemos −4 = 2B, de donde B = −2, y por último D = 1, así 31 1. Métodos de integración Z x+2 dx = A x3 + x Z 1 dx + x Z Bx + D dx = A x2 + 1 Z dx +B x Z xdx +D x2 + 1 Z dx +1 x2 1 = 2 ln |x| − 2 ln(x2 + 1) + arctan x + C 2 = 2 ln |x| − ln(x2 + 1) + arctan x + C. (ii) x4 dx. x4 − 1 Observemos que Grado P (x) = Grado Q(x), pero 1 x4 =1+ 4 , así 4 x −1 x −1 Z Z Z Z x4 1 1 dx = dx + = 1+ 4 dx. 4 4 x −1 x −1 x −1 Z Para la integral Z x4 1 dx aplicamos el método de fracciones simples. −1 Observemos que Q(x) = x4 − 1 = (x2 − 1)(x2 + 1) = (x − 1)(x + 1)(x2 + 1). x4 1 1 A B Dx + E = = + + 2 2 −1 (x − 1)(x + 1)(x + 1) x−1 x+1 x +1 = A(x + 1)(x2 + 1) + B(x − 1)(x2 + 1) + (Dx + E)(x − 1)(x + 1) . (x − 1)(x + 1)(x2 + 1) Igualando los numeradores tenemos: 1 = A(x + 1)(x2 + 1) + B(x − 1)(x2 + 1) + (Dx + E)(x − 1)(x + 1) (1.14) Damos valores a x que anulen los denominadores y los sustituimos en (1.14). 1 Para x = 1 obtenemos 1 = A(2)(2), y de aquí A = . 4 1 Para x = −1 obtenemos 1 = B(−2)(2), y de aquí B = − . 4 Damos ahora a x un valor arbitrario, distinto del anterior, y lo sustituimos en (1.14). Para x = 0 obtenemos 1 = A(1)(1) + B(−1)(1) + E(−1)(1), y de aquí 1 E=− . 2 32 1.5. Integración de funciones Racionales P(x) Q(x) Para x = 2 obtenemos 1 = A(3)(5) + B(1)(5) + (D(2) + E)(1)(3), y de aquí D = 0. Así Z x4 dx = x4 − 1 Z dx + Z x4 1 dx −1 dx +B x−1 Dx + E dx x2 + 1 Z Z Z Z 1 dx dx dx 1 1 = dx + − − 2 4 x−1 4 x+1 2 x +1 = Z dx + A = x+ Z Z dx + x+1 Z 1 1 1 ln |x − 1| − ln |x + 1| − arctan x + C. 4 4 2 Observación 1.5.4 Hasta ahora hemos visto dos ejemplos donde el factor cuadrático es (x2 + 1). Con este factor, la integral que resulta es inmediata ya que obtenemos: Z dx = arctan x + C, x2 + 1 pero ¿Qué pasa cuando el factor cuadrático no es x2 + 1?. Puede pasar lo siguiente: 1. Que el factor irreducible sea de la forma x2 + a, donde a ∈ R con a > 0. En este caso obtenemos la integral: √ Z a x dx = arctan √ + C. 2 x +a a a Z dx = x2 + a Z x2 a dx 1 = a +1 a Z √x a dx 2 . +1 √ x Llamemos t = √ , de donde obtenemos a dt = dx, así a √ √ Z Z √ Z 1 adt a a dx 1 x dx = = = arctan t + C = arctan √ + C. 2 2 2 x +a a a t +1 a a a √x +1 a Ejemplo 1.5.6 (i) x3 + 3x2 + 5x + 7 dx. x2 + 2 Observemos que Grado P (x) > Grado Q(x). Pero Z 3x + 1 x3 + 3x2 + 5x + 7 =x+3+ 2 . 2 x +2 x +2 33 1. Métodos de integración Z x3 + 3x2 + 5x + 7 dx = x2 + 2 Z 3x + 1 dx x+3+ 2 x +2 Z Z Z Z x dx = xdx + 3 dx + 3 dx + 2 2 x +2 x +2 √ x2 3 2 x = + 3x + ln |x2 + 2| + arctan √ + C. 2 2 2 2 Así (ii) x3 + x + 1 dx. x4 − 81 Observemos que Q(x) = x4 − 81 = (x − 3)(x + 3)(x2 + 9). Z x3 + x + 1 A B Dx + E x3 + x + 1 = = + + x4 − 81 (x − 3)(x + 3)(x2 + 9) x−3 x+3 x2 + 9 = A(x + 3)(x2 + 9) + B(x − 3)(x2 + 9) + (Dx + E)(x − 3)(x + 3) (x − 3)(x + 3)(x2 + 9) Igualando los numeradores tenemos: x3 + x + 1 = A(x + 3)(x2 + 9) + B(x − 3)(x2 + 9) + (Dx + E)(x − 3)(x + 3) (1.15) Damos valores a x que anulen los denominadores y los sustituimos en (1.15). Para x = 3 obtenemos 31 = A(6)(18),y de aquí A = 31 . 108 Para x = −3 obtenemos −29 = B(−6)(18), y de aquí B = 29 . 108 Damos ahora a x un valor arbitrario, distinto de los anteriores, y lo sustituimos en (1.15). Para x = 0 obtenemos 1 = A(3)(9) + B(−3)(9) + E(−3)(3) de aquí 4 1 , y finalmente D = . Así 18 9 Z Z Z Z Z 3 dx dx xdx dx x +x+1 dx = A +B +D +E 4 2 2 x − 81 x−3 x+3 x +9 x +9 Z Z Z Z 31 dx dx xdx dx 29 4 1 = + + − 2 2 108 x − 3 108 x+3 9 x + 9 18 x +9 De esta manera, E = − = 29 41 31 ln |x − 3| + ln |x + 3| + ln |x2 + 9| 108 108 92 √ 1 9 x − arctan √ + C. 8 9 9 34 1.5. Integración de funciones Racionales P(x) Q(x) 2. Que el factor irreducible sea de la forma x2 + bx + c, donde b, c ∈ R. En este caso hacemos la completación de cuadrado para obtener la integral. Z dx = 2 x + bx + c Z √ m dx = arctan b 2 m (x + 2 ) + m x + 2b √ m ! + C, donde m es el término independiente que resulta de la completación de cuadrado. Ejemplo 1.5.7 Z dx = x2 + x + 5 Z dx (x + 1 2 ) 2 + 19 4 = q 19 4 19 4 x+ arctan q 1 2 19 4 + C. Observación 1.5.5 Cuando el factor irreducible es de la forma x2 +bx+c en la integral Z Dx + E tenemos que 2 x + bx + c Z Dx + E D dx = 2 x + bx + c 2 D = 2 D = 2 Z Z 2x dx + E 2 x + bx + c 2x + b − b dx + E x2 + bx + c Z Z dx + bx + c x2 dx + bx + c Z dx dx +E 2 2 x + bx + c x + bx + c Z Z D 2x + b dx 2E − Db = dx + , 2 2 2 x + bx + c 2 x + bx + c Z 2x + b Db dx − 2 x + bx + c 2 x2 Z obteniendo así dos integrales inmediatas. Ejemplo 1.5.8 Z dx x5 − x2 Notemos que al factorizar el denominador tenemos que: x5 1 A B C Dx + E 1 = 2 = 2+ + + 2 2 2 −x x (x − 1)(x + x + 1) x x x−1 x +x+1 Por el método de los coeficientes indeterminados obtenemos que A = −1, B = 0, C = 1 1 E= D=− 3 3 35 1. Métodos de integración Así: Z 1.5.2.4. 1 dx = x5 − x2 3 Z dx − x−1 Z 1 = 3 Z dx − x−1 Z = 1 1 ln |x − 1| + 3 x = 1 1 ln |x − 1| + 3 x = 1 1 ln |x − 1| + 3 x − 13 x + 31 dx x2 + x + 1 Z Z 2 + 31 2x + 1 dx dx 1 3 − dx + 2 2 2 x 6 x +x+1 2 x +x+1 Z dx 1 1 − ln |x2 + x + 1| + 2 6 2 x + 12 + 34 q 3 1 x+ 1 1 4 q 2 − ln |x2 + x + 1| + 3 arctan 6 2 4 3 4 √ 3 1 2x + 1 2 √ +C − ln |x + x + 1| + arctan 6 3 3 dx + x2 Z Caso 4: Cuando Q(x) se factoriza como producto de factores cuadráticos repetidos. En este caso es recomendable un cambio de variable. Ejemplo 1.5.9 Z dx . (x2 + 9)2 Llamemos x2 = 9 tan2 t, de donde x = 3 tan t y de aquí obtenemos dx = 3 sec2 tdt, así Z Z Z dt 1 3 sec2 tdt 3 sec2 tdt = = 2 2 (9 tan t + 9)2 81(tan t + 1)2 27 sec2 t Z Z Z Z 1 1 + cos(2t) 1 1 1 2 cos tdt = dt + cos(2t)dt dt = = 27 27 2 54 54 x 1 1 sen(2t) 1 = + t+ +C = arctan (sent)(cos t) + C 54 108 54 3 108 x 1 x 3 1 + +C arctan = 54 3 108 x2 + 9 x2 + 9 x 1 3x = + arctan + C. 54 3 108(x2 + 9)2 dx = (x2 + 9)2 Z Observación 1.5.6 ZEn este caso puede usarse una fórmula de recurrencia que deduciremos dx . Integremos por parte. a continuación. Sea 2 (x + a2 )n u= (x2 1 −2nxdx −→ du = 2 2 n +a ) (x + a2 )n+1 dv = dx −→ v = x 36 1.5. Integración de funciones Racionales P(x) Q(x) Así Z x dx = + 2n (x2 + a2 )n (x2 + a2 )n x = + 2n (x2 + a2 )n Z Z x2 dx (x2 + a2 )n+1 (x2 + a2 ) − a2 dx (x2 + a2 )n+1 Z 1 1 2 dx − 2na dx 2 2 n 2 (x + a ) (x + a2 )n+1 Z Z x dx dx 2 = + 2n − 2na 2 2 n 2 2 n 2 (x + a ) (x + a ) (x + a2 )n+1 x + 2n = 2 (x + a2 )n de donde Z Z dx x 2n − 1 dx = + 2 2 n+1 2 2 2 n 2 2 (x + a ) 2na (x + a ) 2na (x + a2 )n la cual es la fórmula que usaremos para el cálculo de las integrales en este caso. Z (1.16) Ejemplo 1.5.10 Z dx . (i) 2 (x + 1)2 En este caso n = 1 y por la fórmula (1.16) tenemos: Z (ii) Z dx x 1 = + 2 2 2 (x + 1) 2(x + 1) 2 Z dx x 1 = + arctan x + C. 2 +1 2(x + 1) 2 x2 x−1 . (x2 + 2x + 3)2 Completando cuadrado tenemos: x2 + 2x + 3 = (x + 1)2 + 2 Llamemos t = x + 1, de donde t − 2 = x − 1 y de quí obtenemos dt = dx, así Z x−1 dx = 2 (x + 2x + 3)2 = = = = Z x−1 t−2 dx = dt 2 2 2 [(x + 1) + 2] (t + 2)2 Z Z t dt dt − 2 2 2 2 (t + 2) (t + 2)2 Z Z dt 2 −2 (t + 2) tdt − 2 2 (t + 2)2 Z 1 dt − (t2 + 1)−1 − 2 2 (t2 + 2)2 Z 1 dt − 2 −2 2 2(t + 2) (t + 2)2 Z 37 1. Métodos de integración dt , donde n = 1 tenemos: + 2)2 √ Z Z dt dt t 1 t 1 2 t = + = + arctan √ + C. 2 2 2 2 2 (t + 2) 2 · 2(t + 2) 2 · 2 t +2 4(t + 2) 4 2 2 Por otro lado, aplicando la fórmula (1.16) a Z (t2 Así Z (x2 1 x−1 =− −2 2 + 2x + 3) 2[(x + 1)2 + 2]2 1 2 x+1 x+1 + arctan √ 2 4[(x + 1) + 2] 4 2 2 Observación 1.5.7 Por lo general las integrales que aparecen son: mula (1.16) se reduce a: Z dx x 1 = 2 2 + 2 2 2 2 2 (x + a ) 2a (x + a ) 2a Z (x2 √ Z (x2 ! + C. dx , así la fór+ a2 )2 dx x 1 x = 2 2 + 3 arctan + C. 2 2 +a ) 2a (x + a ) 2a a Ejemplo 1.5.11 Z dx . 2 (x + 9)2 Por la fórmula anterior tenemos: Z (x2 1.5.3. dx x 1 x x 1 x = + arctan + C = + arctan + C. 2 2 2 + 9) 2 · 9(x + 9) 2 · 27 3 18(x + 9) 54 3 Cambios que conducen a integrales de fracciones racionales Aplicamos ahora el método de fracciones simples para el cálculo de algunas integrales mediante un cambio de variable apropiado. 1.5.3.1. Con funciones exponenciales. Ejemplo 1.5.12 (i) Z 1 + ex dx = 1 − ex Z 1 + ex x e dx. ex (1 − ex ) Llamemos t = ex , de donde obtenemos dt = ex dx, y notemos que t 6= 0 pues ex 6= 0, para todo x real. Así Z Z 1 + ex x 1+t e dx = dt. x x e (1 − e ) t(1 − t) 38 1.5. Integración de funciones Racionales P(x) Q(x) Observemos que: A B A(1 − t) + Bt 1+t = + = . t(1 − t) t 1−t t(1 − t) Igualando los numeradores tenemos: (1.17) 1 + t = A(1 − t) + Bt. Damos valores a xque anulen los denominadores y los sustituimos en (1.17). Para x = 1 obtenemos 2 = B(1), y de aquí B = 2. Para x = 0 obtenemos 1 = A(1), y de aquí A = 1. Así Z 1 + ex x e dx = ex (1 − ex ) Z 1+t dt = A t(1 − t) Z 1 dt + B t Z 1 dt 1−t = ln |t| − 2 ln |1 − t| + C = ln |ex | − 2 ln |1 − ex | + C = x − 2 ln |1 − ex | + C. Z ex 1 dx = dx. (ii) ex + e−x e2x + 1 Llamemos t = ex , de donde obtenemos dt = ex dx. Así Z Z Z 1 ex dt dx = dx = = arctan t + C = arctan ex + C. x −x 2x 2 e +e e +1 t +1 Z 1.5.3.2. Con funciones trigonométricas. En el cálculo de integrales de funciones trigonométricas combinada mediante suma, multiplicación y división, una sustitución muy útil que transforma estas funciones en función racional es: √ t2 + 1 t x 2 1 x t = tan , 2 x = arctan t, 2 donde dx = 2 dt. 1 + t2 Esta situación lleva a la expresión: senx = 2t , 1 + t2 y cos x = 1 − t2 . 1 + t2 En efecto. Escribamos: x x x t 2t 1 √ = 2sen cos = 2√ ,y senx = sen 2 = 2 2 2 2 2 2 t +1 t +1 t +1 39 1. Métodos de integración x x x 1 t2 1 − t2 = cos2 − sen2 = 2 − 2 = 2 . cos x = cos 2 2 2 2 t +1 t +1 t +1 Ejemplo 1.5.13 Z dx (i) 1 + senx Z dx = 1 + senx Z = 2 (ii) Z 1 Z 2 1+t2 2t + 1+t 2 dt = (t + 1)−2 dt = dx 3 + 5senx Z Z dx = 3 + 5senx Z 2 dt = 2 1 + 2t + t2 Z dt =2 2 t + 2t + 1 −2 −2 x + C. +C = t+1 +1 tan 2 2 1+t2 3+ 2t 5 1+t 2 dt = 2 Z 3t2 Z dt . + 10t + 3 Observemos que: 3t2 1 1 A B = = + . + 10t + 3 (t + 3)(3t + 1) t + 3 3t + 1 1 3 y B = . Así 8 8 Z Z Z Z dt dt dt dx = 2 = 2A + 2B 2 3 + 5senx 3t + 10t + 3 t+3 3t + 1 Calculando los coeficientes tenemos: A = − 2 6 1 = − ln |t + 3| + · ln |3t + 1| + C 8 8 3 1 x 1 x = − ln tan + 3 + ln 3 tan + 1 + C. 4 2 4 2 (iii) Z dx 3senx + 4 cos x Z dx = 3senx + 4 cos x Observemos que: 2t2 Z 3 2 1+ t2 2t −4 1 + t2 2 1−t 1 + t2 dt = − Z 2t2 1 A B 1 = = + . − 3t − 2 (t − 2)(2t + 1) t − 2 2t + 1 dt − 3t − 2 dt (t + 1)2 40 1.5. Integración de funciones Racionales P(x) Q(x) 2 1 y B = − . Así 5 5 Z Z Z Z dt dt dt dx = − = −A −B 2 3senx + 4 cos x 2t − 3t − 2 t−2 2t + 1 Calculando los coeficientes tenemos: A = 1 2 1 = − ln |t − 2| + · ln |2t + 1| + C 5 5 2 1 x 1 x = − ln tan − 2 + ln 2 tan + 1 + C. 5 2 5 2 1.5.3.3. Con funciones radicales con distintos índices. En el cálculo de integrales de funciones radicales combinada mediante suma, multiplicación y división, se considera el cambio tm , donde m es el mínimo común múltiplo de los índices de las raices vinculadas en la expresión. Ejemplo 1.5.14 (i) Z √ 4 x−1 √ dx. 3+ x−1 Primero hacemos un cambio de variable. Llamemos x − 1 = t4 , de donde obtenemos dx = 4t3 dt, así Z √ 4 x−1 √ dx = 3+ x−1 Z t 4t3 dt = 4 3 + t2 Z t4 dt. 3 + t2 t4 dt hacemos la división de polinomios y obtenemos: 3 + t2 Z Z Z Z Z 1 t4 9 2 2 dt = 4 t dt + 12 dt − 36 4 dt = 4 t +3− 2 dt 2 2 3+t t +3 t +3 En la integral 4 Z √ 36 3 t t3 +C arctan √ = 4 + 3t − 3 3 3 √ √ √ 4 √ ( 4 x − 1)3 36 3 x−1 4 √ =4 + 3( x − 1) − arctan + C. 3 3 3 Sustituyendo en la ecuación anterior tenemos: Z √ 4 x−1 √ dx = 4 3+ x−1 √ 4 x−1 3 3 +3 √ 4 √ √ 4 x−1 36 3 √ arctan + C. x−1 − 3 3 41 1. Métodos de integración (ii) Z √ 6 x √ dx. 1+ 3x Llamemos x = t6 , de donde obtenemos dx = 6t5 dt. Luego Z √ 6 √ 6 Z Z t6 1 t6 4 2 5 √ dt = 6 t −t +1− dt 6t dt = 6 3 1 + t2 1 + t2 1 + t6 Z Z Z Z 1 4 2 dt = 6 t dt − 6 t dt + 6 dt − 6 1 + t2 5 3 t t = 6 −6 + 6t + arctan t + C 5 3 √ √ √ 6√ 6 6 = x5 − 2 x3 + 6 6 x + arctan( 6 x) + C. 5 x √ dx = 1+ 3x Z 1.6. Integración De Funciones Trigonométricas 1.6.1. Integrales de la forma: Z 1.6.2. Si n es par. Z senn xdx y cosn xdx. De ser este el caso, usaremos las identidades trigonométricas: sen2 x = 1 − cos(2x) 2 y cos2 x = 1 + cos(2x) . 2 Ejemplo 1.6.1 (i) Z sen2 xdx. Como n es par (n = 2) reemplazamos sen2 x = Z 2 sen xdx = = Z 1 − cos(2x) . 2 1 1 − cos(2x) dx = 2 2 Z 1 dx − 2 Z cos(2x) 1 1 sen(2x) 1 1 x− · + C = x − sen(2x) + C. 2 2 2 2 4 42 1.6. Integración De Funciones Trigonométricas (ii) Z cos4 xdx. Como n es par (n = 4) reemplazamos 4 cos x = Z cos4 xdx = = = = = 2 1 + cos(2x) 1 = (1 + 2 cos(2x) + cos2 (2x)). 2 4 Z Z Z 1 2 dx + 2 cos(2x)dx + cos (2x)dx 4 Z 1 2 sen(2x) 1 cos2 (2x) x+ · + 4 4 2 4 Z 1 1 + cos(4x) 2 sen(2x) 1 x+ · + dx 4 4 2 4 2 Z Z 1 2 sen(2x) 1 1 1 dx + cos(4x)dx x+ · + 4 4 2 4 2 2 2 sen(2x) 1 1 1 sen(4x) 1 +C x+ · + x+ · 4 4 2 4 2 2 4 De esta manera Z 1.6.2.1. 3 1 1 cos4 xdx = x + sen(2x) + sen(4x) + C. 8 4 32 Si n es impar. Usaremos la identidad sen2 x + cos2 x = 1 y separamos. Z Z Z Z n n−1 n sen (x)dx = sen (x)sen(x)dx ó cos (x)dx = cosn−1 (x) cos(x)dx. Ejemplo 1.6.2 (i) Z sen3 xdx. Como n es impar (n = 3) reemplazamos. Usamos sen2 x + cos2 x = 1, de donde sen2 x = 1 − cos2 x. Así Z Z Z 3 2 sen xdx = (sen x)senxdx = (1 − cos2 x)senxdx = Z senxdx − Z (cos2 x)senxdx = − cos x − cos3 x + C. 3 43 1. Métodos de integración (ii) Z cos5 xdx. Z 5 cos xdx = = = Z Z Z 4 (cos x) cos xdx = Z (1 − sen2 x)2 cos xdx (1 − 2sen2 x + sen4 x) cos xdx cos xdx − 2 Z 2 (sen x) cos xdx + sen3 x sen5 x = senx − 2 + + C. 3 4 1.6.3. Integrales de la forma: 1.6.3.1. Si m ó n es impar. Z Z (sen4 x) cos xdx (senm x)(cosn x)dx. Si m ó n es impar, se trabaja con el menor impar de la misma forma que en el caso anterior sustituyendo solo una de la funciones. Ejemplo 1.6.3 (i) Z (sen5 x)(cos3 x)dx. Como n = 3 es el menor impar reemplazamos cos2 x = 1 − sen2 x. Así Z Z Z 5 3 2 5 (sen x)(cos x)dx = (cos x)(cos x)(sen x)dx = (1 − sen2 x)(cos x)(sen5 x)dx = (ii) Z Z 5 (sen x) cos xdx − Z (sen7 x) cos xdx = sen6 x sen8 x − + C. 6 8 (sen3 x)(cos2 x)dx. Como m = 3 es el único impar reemplazamos sen2 x = 1 − cos2 x. De esta manera Z Z Z 3 2 2 2 (sen x)(cos x)dx = (sen x)(senx)(cos x)dx = (1 − cos2 x)(senx)(cos2 x)dx = Z 2 (cos x)senxdx − Z (cos4 x)senxdx = cos3 x cos5 x − + C. 3 5 44 1.6. Integración De Funciones Trigonométricas (iii) Z sen3 x √ dx. cos x 3 cos x Como m = 3 es el único impar reemplazamos sen2 x = 1 − cos2 x. Así tenemos: Z sen3 x √ dx = cos x 3 cos x = = Z Z Z 3 (sen x)(cos x)dx = Z 4 (sen2 x)(senx)(cos− 3 x)dx 4 (1 − cos2 x)(senx)(cos− 3 x)dx − 34 (cos x)senxdx − 1 = 3 cos− 3 x − 1.6.3.2. − 43 Z 2 (cos 3 x)senxdx 5 3 3 3√ 3 cos5 x + C. cos 3 x + C = − √ − 3 5 cos x 5 Si m y n son pares e iguales. Si m y n son pares e iguales se hace el cámbio: n n (sen x)(cos x) = 1 sen(2x) 2 n , pues sen(2x) = 2senx cos x, deduciéndose de aquí la ecuación anterior. Ejemplo 1.6.4 Z (sen2 x)(cos2 x)dx Z 1.6.3.3. (i) Z Z 1 1 − cos(4x) sen (2x)dx = dx 4 2 Z Z 1 1 1 1 dx − cos(4x)dx = x − sen(4x) + C. = 8 8 8 32 1 (sen x)(cos x)dx = 4 2 2 Z 2 Si m y n son pares y distintos. (sen4 x)(cos6 x)dx 45 1. Métodos de integración Z 4 6 (sen x)(cos x)dx = = = = = = = = (ii) Z 4 4 2 3 1 1 sen5 (2x) x+ sen(3x) − sen(4x) + + C. 256 2048 256 320 (cos4 x)(sen2 x)dx Z Z Z 1 + cos(2x) sen2 (2x) 4 2 2 2 2 (cos x)(sen x)dx = (cos x)(cos x)(sen x)dx = dx 2 2 Z Z 1 1 2 sen (2x)dx + sen2 (2x) cos(2x)dx = 4 4 Z 1 1 − cos(4x) 1 sen3 (2x) = dx + +C 4 2 4 2·3 = 1.6.4. Z 1 sen4 (2x) cos2 xdx (sen x)(cos x)(cos x)dx = 16 Z 1 + cos(2x) 1 4 sen (2x) dx 16 2 Z Z 1 1 4 sen (2x)dx + sen4 (2x) cos(2x)dx 32 32 Z 1 1 sen5 (2x) sen4 (2x)dx + · 32 64 5 2 Z 1 1 − cos(4x) 1 sen5 (2x) dx + · 32 2 64 5 Z Z Z 1 1 1 sen5 (2x) dx − cos(4x)dx + cos2 (4x)dx + 128 64 128 320 Z 1 1 + cos(8x) 1 1 sen5 (2x) x− sen(4x) + dx + 128 256 128 2 320 Z 1 1 1 x − sen(2x) + sen3 (2x) + C 8 16 24 Integrales de la forma: Z tann xdx. En este caso se descompone tann x = (tan2 x)(tann−2 x) y se sustituye tan2 x = sec2 x − 1. Ejemplo 1.6.5 Z (i) tan2 xdx. Z Z Z Z 2 2 2 tan xdx = (sec x − 1)dx = sec xdx − dx = tan x − x + C. 46 (ii) 1.6. Integración De Funciones Trigonométricas Z tan3 xdx. Z Z Z 3 2 tan xdx = (tan x)(tan x)dx = (sec2 x − 1) tan xdx = (iii) Z Z 2 (sec x) tan x − Z tan2 x + ln | cos x| + C. 2 tan xdx = tan4 xdx Z tan xdx = Z = Z 4 = 2 2 2 2 (tan x)(tan x)dx = (tan x)(sec x)dx − Z Z (sec2 x − 1) tan2 xdx tan3 x tan xdx = − 3 2 tan3 x − tan x + x + C. 3 Z (sec2 x − 1)dx Observación 1.6.1 Éstas integrales se resuelven también haciendo un cambio de variable conveniente. Es recomendable hacerla de esta manera ya que es más rápido y no requieren de destreza en trigonometría. Ejemplo 1.6.6 (i) Z tan4 xdx Llamemos t = tan x. Así, arctan t = x, obteniéndose que sigue que Z Como 4 tan xdx = Z 1 dt = dx. De aquí se 1 + t2 t4 dt t2 + 1 t4 1 = (t2 − 1) + 2 2 t +1 t +1 se tiene que Z 4 tan xdx = Z t4 dt = t2 + 1 Z 2 t dt − Z dt + Z dt t2 + 1 = tan3 x t3 − t + arctan t = − tan x + arctan(tan x) + C 3 3 = tan3 x − tan x + x + C 3 47 1. Métodos de integración (ii) Z tan7 xdx. Análogamente al ejemplo anterior, llamemos t = tan x, de donde arctan t = x. De aquí 1 dt = dx, y de esta forma 1 + t2 Z Z Z 1 t 7 7 5 3 tan xdx = t dt = dt t −t +t− 1 + t2 1 + t2 = t6 t4 t2 1 − + − ln |1 + t2 | + C 6 4 2 2 = tan6 x tan4 x tan2 x 1 − + − ln |1 + tan2 x| + C. 6 4 2 2 Es decir, para éste caso es siempre conveniente hacer el cambio de variable t = tan x y dt dx = , obteniendo así 1 + t2 Z Z tn n dt tan x = 1 + t2 1.6.5. Integrales de la forma: 1.6.5.1. Si n es par. Z secn xdx. En este caso se descompone secn x = (sec2 x)(secn−2 x) y se sustituye sec2 x = 1 + tan2 x. Ejemplo 1.6.7 Z (i) sec2 xdx (ii) Z Z sec4 xdx Z Z Z 4 2 2 sec xdx = (sec x)(sec x)dx = (1 + tan2 x)(sec2 x)dx = 1.6.6. sec2 xdx = tan x + C. (Inmediata) Z 2 sec xdx + Z (tan2 x)(sec2 x)dx = tan x + tan3 x + C. 3 Si n es impar. En este caso se usa el método de integración por parte.En este caso hay que tener presente que las integrales resultantes son cíclicas 48 1.6. Integración De Funciones Trigonométricas Z Ejemplo 1.6.8 sec3 xdx Z 3 sec xdx = Z (sec2 )(sec x)dx. Tomemos u = sec x −→ du = (sec x)(tan x)dx dv = sec2 xdx −→ v = tan x. Así Z 3 sec xdx = Z 2 (sec )(sec x)dx = (sec x)(tan x) − = (sec x)(tan x) − = (sec x)(tan x) − Z Z Z (tan2 x)(sec x)dx (sec2 x − 1) sec xdx 3 sec xdx − Z sec xdx Observemos que después de aplicar el método llegamos a la integral inicial. Entonces tratamos la expresión como una ecuación. Z Z 3 2 sec xdx = (sec x)(tan x) − sec xdx, así Z 1.6.7. sec3 xdx = (sec x)(tan x) − ln | sec x + tan x| + C. 2 Integrales de la forma: Z (tann x)(secm x)dx. Z sec xdx. Ejemplo 1.6.9 (i) Z (ii) Z (tan x)(sec x)dx = (iii) Z (tan3 x)(sec2 x)dx = (tan x)(sec x)dx = sec x + C. 2 Z 3 sec xdx − tan4 x + C. 4 Observación 1.6.2 En este caso intentamos escribir el integrando como función de tann x con sec2 x como su derivada derivada, o como función de secn x con (sec x)(tan x) como su derivada . 49 1. Métodos de integración (iv) Z (tan3 x)(sec3 x)dx Z 3 3 (tan x)(sec x)dx = = = = (v) Z Z Z Z (tan2 x)(sec3 x)(tan x)dx (sec2 x − 1)(sec2 x)(tan x)(sec x)dx 4 (sec x)(tan x)(sec x)dx − sec5 x sec3 x − + C. 5 3 Z (sec2 x)(tan x)(sec x)dx (tan4 x)(sec6 x)dx Z 4 6 (tan x)(sec x)dx = = = = Z Z Z Z + = (tan4 x)(sec4 x)(sec2 x)dx (tan4 x)(tan2 x + 1)2 (sec2 x)dx (tan4 x)(tan4 x + 2 tan2 x + 1)(sec2 x)dx 8 2 (tan x)(sec x)dx + 2 Z Z (tan6 x)(sec2 x)dx (tan4 x)(sec2 x)dx tan9 x tan7 x tan5 x +2 + + C. 9 7 5 En el ejemplo anterior se puede notar que para las integrales de la forma se tiene que: Z (tann x)(secm x)dx 1. Si n es par, se reserva sec2 . 2. Si n y m son ambos impares, se reserva sec x tan x y se lleva todo a sec x. 3. Si m es par y n es impar, se lleva todo a sec x. 1.6.8. Integrales de la forma: R R R sen(mx) cos(nx)dx, sen(mx)sen(nx)dx, cos(mx) cos(nx)dx. En cada uno de los casos se usa la fórmula correspondiente. 50 1.6. Integración De Funciones Trigonométricas 1 1. sen(mx) cos(nx) = [sen(m − n)x − sen(m + n)x]. 2 1 2. sen(mx)sen(nx) = [cos(m − n)x − cos(m + n)x]. 2 1 3. cos(mx) cos(nx) = [cos(m − n)x + cos(m + n)x]. 2 Ejemplo 1.6.10 (i) Z sen(5x) cos(8x)dx Z (ii) Z Z 1 sen(5x) cos(8x)dx = 2 Z 1 = − 2 [sen(−3x) + sen(13x)]dx Z 1 sen(3x)dx + 2 Z sen(13x)dx = 1 cos(3x) 1 cos(13x) · − · +C 2 3 2 13 = 1 1 cos(3x) − cos(13x) + C. 6 26 cos(x) cos(2x) cos(5x)dx cos(x) cos(2x) cos(5x)dx = Z 1 = 2 [cos(x) cos(2x)] cos(5x)dx Z 1 = − 2 1 = − 4 1 + 4 1 = − 4 1 + 4 = [cos(−x) + cos(3x)] cos(5x)dx Z Z Z Z Z 1 cos(x) cos(5x)dx + 2 Z cos(3x) cos(5x)dx [cos(−4x) + cos(6x)]dx [cos(−2x) + cos(8x)]dx 1 cos(4x)dx + 4 Z 1 cos(−2x)dx + 4 Z cos(6x)dx cos(8x)dx 1 1 1 1 sen(4x) + sen(6x) − sen(−2x) + sen(8x) + C. 16 24 8 32 51 1. Métodos de integración 1.7. Integración Por Sustituciones Trigonométricas Calcularemos integrales de la forma Z f (x, √ ±a2 ± b2 x2 dx). √ a a2 − b2 x2 hacemos el cambio x = sent. b √ a (b) Si a2 + b2 x2 hacemos el cambio x = tan t. b p a (c) Si b2 (x2 − a2 ) hacemos el cambio x = sec t. b (a) Si Ejemplo 1.7.1 (i) Z √ 9 − x2 dx. x Hacemos el cambio de variable x = 3sent, de donde dx = 3 cos tdt, así Z √ Z √ Z √ 9 − 9sen2 t 3 1 − sen2 t 3 cos tdt = 3 cos tdt 3sent 3sent Z √ 2 Z Z cos t cos tdt cos2 t 1 − sen2 t = 3 =3 dt = 3 dt sent sent sent Z Z Z 1 dt − 3 sentdt = 3 csc tdt + 3 cos t + C = 3 sent 9 − x2 dx = x = 3 ln | csc t + cot t| + 3 cos t + C. Por último cambiamos nuevamente a la variable original de la siguiente manera. Si x = 3sent, enx = sent y esto nos sugiere la construcción tonces 3 del siguiente triángulo: x 3 t √ 9 − x2 √ √ 9 − x2 9 − x2 3 Así cos t = , csc t = y cot t = . Finalmente 3 x x √ √ Z √ x 9 − x2 9 − x2 9 − x2 +3 dx = 3 ln + + C. x 3 x 3 Z dx √ . (ii) x 4 + x2 Hacemos el cambio de variable x = 2 tan t, de donde dx = 2 sec2 tdt, así 52 1.7. Integración Por Sustituciones Trigonométricas Z Z 1 sec2 t 2 sec2 tdt √ √ = dt 2 2 tan t 4 + 4 tan2 t tan t 1 + tan2 t Z Z Z Z sec2 t sec t dt 1 1 1 1 √ csc tdt dt = = = dt = 2 2 tan t 2 sent 2 tan t sec2 t 1 = − ln | csc t + cot t| + C. 2 dx √ = x 4 + x2 Z Por último cambiamos nuevamente a la variable original de la siguiente manera. Si x = 2 tan t enx tonces = tan t y esto nos sugiere la construcción 2 del siguiente triángulo: Así csc t = (iii) Z √ √ √ 4 + x2 x t 2 4 + x2 2 y cot t = . Finalmente x x √ Z dx 4 + x2 2 1 √ + + C. = − ln 2 x x x 4 + x2 x2 dx. x2 − 25 Hacemos el cambio de variable x = 5 sec t, de donde dx = 5(sec t)(tan t)dt. Así Z Z Z 25(sec2 t)5(sec t)(tan t)dt 5(sec3 t)(tan t)dt x2 √ √ √ dx = = 25 dt x2 − 25 25 sec2 t − 25 5 sec2 t − 1 Z Z (sec3 t)(tan t) √ dt = 25 sec3 tdt = 25 2 tan t 25(sec t)(tan t) − ln | sec t + tan t| + C. = 2 Por último cambiamos nuevamente a la variable original de la siguiente manera. Si x = x 5 sec t, entonces = sec t y esto nos sugiere 5 la construcción del siguiente triángulo: Así tan t = √ √ x2 − 25 x t 5 x2 − 25 . Finalmente 5 √ √ Z x2 − 25 x2 − 25 x 25 x x2 √ · − ln + + C. dx = 2 5 5 5 5 x2 − 25 53 1. Métodos de integración Observación 1.7.1 Cuando la función sub-radical es un trinomio de segundo grado (mx2 + nx + d), lo transformamos en una suma o resta de cuadrados mediante la completación de cuadrado, es decir: mx2 + nx + d = (x ± a)2 ± c donde a = n2 n y c= + d. 2 4 Ejemplo 1.7.2 (i) Z √ x2 − 6x − 7dx. Observemos que x2 − 6x − 7 = (x − 3)2 − 16, así obtenemos Z √ Z p 2 x − 6x − 7dx = (x − 3)2 − 16dx. Ahora hacemos el cambio de variable x − 3 = 4 sec t, de donde dx = 4(sec t)(tan t)dt. Así Z √ x2 − 6x − 7dx = Z p = 16 = 16 = 16 = (x − Z √ Z Z 3)2 − 16dx = Z √ 16 sec2 t − 16(4 sec t)(tan t)dt sec2 t − 1(sec t)(tan t)dt = 16 2 (tan t)(sec t)dt = 16 3 sec tdt − 16 Z Z Z (tan t)(sec t)(tan t)dt (sec2 t − 1)(sec t)dt sec tdt 16[(sec t)(tan t) − ln | sec t + tan t|] − 16 ln | sec t + tan t| + C 2 = 8(sec t)(tan t) − 24 ln | sec t + tan t| + C. Por último cambiamos nuevamente a la p x−3 variable original de la siguiente manera. (x − 3)2 − 16 x−3 Si x−3 = 4 sec t, entonces = sec t t 4 y esto nos sugiere la construcción del 4 siguiente triángulo: p (x − 3)2 − 16 . Finalmente Así tan t = 4 p p Z √ 2 − 16 (x − 3) (x − 3)2 − 16 8(x − 3) x − 3 x2 − 6x − 7dx = + C. − 24 ln + 4 4 4 4 54 (ii) 1.7. Integración Por Sustituciones Trigonométricas Z √ 3 − 2x − x2 dx. Observemos que −x2 − 2x + 3 = −(x2 + 2x − 3) = −[(x + 1)2 − 4] = 4 − (x + 1)2 . Así obtenemos Z √ Z p 2 3 − 2x − x dx = 4 − (x + 1)2 dx. Ahora hacemos el cambio de variable x + 1 = 2 sen t, de donde dx = 2 cos tdt. De esta forma Z √ Z √ Z p 2 2 3 − 2x − x dx = 4 − (x + 1) dx = 4 − 4sen2 t (2 cos tdt) = 4 = 4 Z √ Z 1 − sen2 t(cos tdt) = 4 1 + cos(2t) dt = 2 2 Z Z √ dt + 2 cos2 t(cos tdt) sen(2t) = 2t + sen(2t) + C 2 = 2t + 2(sent)(cos t) + C Por último cambiamos nuevamente a la variable original de la siguiente manera. Si x + 1 = 2sent, x+1 entonces = sent y esto nos sugiere la cons2 trucción del siguiente triángulo: Así cos t = p Z √ (iii) Z 4 − (x + 1)2 x+1 , sent = y arcsen 2 2 3 − 2x − x2 dx = 2arcsen x+1 2 2 x+1 t p 4 − (x + 1)2 x+1 2 x+1 +2 · 2 = t. Finalmente p 4 − (x + 1)2 + C. 2 dx p . [(x + 1)2 + 4]3 Hacemos el cambio de variable x + 1 = 2 tan t, de donde dx = 2 sec2 tdt. Así Z dx p [(x + 1)2 + 4]3 2 sec2 tdt 2 sec2 tdt p p = 8 (sec2 t)3 (4 tan2 t + 4)3 43 (tan2 t + 1)3 Z Z Z 1 sec2 t dt 1 1 1 = cos tdt = sent + C. dt = = 3 4 sec t 4 sec t 4 4 = Z p = Z 2 sec2 tdt Z 55 1. Métodos de integración Por último cambiamos nuevamente a la variable original de la siguiente manera. Si x + 1 = 2 tan t, x+1 = tan t y esto nos sugiere la consentonces 2 trucción del siguiente triángulo: p (x + 1)2 + 4 x+1 t 2 x+1 . Finalmente (x + 1)2 + 4 Z dx 1 1 x+1 p = sent + C = · p + C. 4 4 [(x + 1)2 + 4]3 (x + 1)2 + 4 Así sent = p 1.8. Integración por sustituciones de Euler Las integrales de la forma Z f (x, √ ax2 + bx + c)dx se calcula haciendo una de las si- guientes sustituciones de Euler: √ √ ax2 + bx + c = t ± x a, √ √ 2. ax2 + bx + c = tx ± c, √ 3. ax2 + bx + c = (x − a)t, del trinomio ax2 + bx + c. 1. si a > 0. si c > 0. si ax2 + bx + c = a(x − α)(x − β), es decir; si α es una raíz Ejemplo 1.8.1 (i) Z 1+ √ dx . + 2x + 2 x2 Como a = 1 > 0, hacemos la sustitución √ x2 + 2x + 2 = t − x. Elevando al cuadrado y haciendo las operaciones correspondientes obtenemos: 2x + 2tx = t2 + 2 de donde x = t2 + 2t + 2 t2 − 2 y dx = dt. De esta manera 2(1 + t) 2(1 + t)2 1+ √ x2 t2 − 2 t2 + 4t + 4 + 2x + 2 = 1 + t − = , 2(1 + t) 2(1 + t) y sustituyendo obtenemos una integral de fracciones simples. Z Z Z 2(t + 1)(t2 + 2t + 2) dx t2 + 2t + 2 √ = dt = dt. (t2 + 4t + 4)2(1 + t)2 (1 + t)(t + 2)2 1 + x2 + 2x + 2 56 1.9. Integrales de la forma: Z xm (a + bxn )p dx, con m, n, p ∈ Q Observemos que t2 + 2t + 2 A B D = + + . 2 (1 + t)(t + 2) t + 1 t + 2 (t + 2)2 Calculando los coeficientes tenemos: A = 1, B = 0, y D = −2. Así Z Z Z Z t2 + 2t + 2 dt dt dx √ = dt = −2 2 (1 + t)(t + 2) t+1 (t + 2)2 1 + x2 + 2x + 2 2 = ln |t + 1| + + C. t+2 Por último cambiamos nuevamente a la variable original x. Z √ dx 2 √ √ = ln x + 1 + x2 + 2x + 2 + + C. 2 1 + x + 2x + 2 x + 2 + x2 + 2x + 2 Z xdx √ . (ii) ( 7x − 10 − x2 )3 En este caso a < 0 y c√< 0. Como 7x −p 10 − x2 tiene raíces reales (α = 2 y β = 5) hacemos la sustitución 7x − 10 − x2 = (x − 2)(5 − x) = (x − 2)t. Elevando al cuadrado y haciendo las operaciones correspondientes obtenemos: 5 − x = (x − 2)t2 de donde x = 5 + 2t2 6tdt y dx = − , así 2 1+t (1 + t2 )2 5 + 2t2 3t (x − 2)t = −2 t= , 2 1+t 1 + t2 y sustituyendo obtenemos la integral: Z Z Z 5 + 2t2 5 2 6 xdx √ dt = − + 2 dt = − 27 t2 9 t2 ( 7x − 10 − x2 )3 5 2 − + 2t + C, = − 9 t donde t= 1.9. 1.9.1. √ Integrales de la forma: 7x − 10 − x2 . x−2 Z xm (a + bxn)pdx, con m, n, p ∈ Q Si p es un número entero. Si p > 0 se desarrolla la fórmula binomial de Newton, pero si p < 0 entonces hacemos x = tk , donde k es el común denominador de las fracciones de m y n. 57 1. Métodos de integración Ejemplo 1.9.1 (i) Z √ 3 x(2 + √ 2 x) dx = Z x1/3 (2 + x1/2 )2 dx. Observemos que p = 2 > 0, así Z Z Z √ √ 2 1/3 1/2 2 3 x(2 + x) dx = x (2 + x ) dx = x1/3 (x + 4x1/2 + 4)dx = (ii) Z Z 24 3 (x4/3 + 4x5/6 + 4x1/3 )dx = x7/3 + x11/6 + 3x4/3 + C. 7 11 x−2/3 (1 + x2/3 )−1 dx. Observemos que p = −1 < 0, por lo tanto hacemos x = t3 donde dx = 3t2 dt. Así Z Z Z 1 −2/3 2/3 −1 −2 2 −1 2 dt = 3 arctan t + C x (1 + x ) dx = x (1 + t ) 3t dt = 3 1 + t2 √ = 3 arctan 3 x + C. 1.9.2. Si m+1 es un número entero. n En este caso hacemos tα = a + bxn , donde α es el denominador de la fracción p. Ejemplo 1.9.2 √ Z p Z 1+ 3x √ dx = x−2/3 (1 + x1/3 )1/2 dx. 3 2 x 1 1 m+1 2 y = 1 es un número entero, entonces Observemos que m = − , n = , p = 3 3 2 n 1 hacemos la sustitución 1 + x1/3 = t2 donde x−2/3 dx = 2tdt. De esta forma 3 Z p 1.9.3. √ Z Z 1+ 3x −2/3 1/3 1/2 √ dx = x (1 + x ) dx = 6 t2 dt = 2t3 + C = 2(1 + x1/3 )3/2 + C. 3 x2 Si m+1 + p es un número entero. n En este caso hacemos a + bxn = tα xn , donde α es el denominador de la fracción p. 58 1.9. Integrales de la forma: Z xm (a + bxn )p dx, con m, n, p ∈ Q Ejemplo 1.9.3 Z Z dx √ = x−11 (1 + x4 )−1/2 dx. 11 4 x 1+x m+1 1 + p = −3 es un número entero, entonces hacemos la Observemos que p = − y 2 n 1 de donde sustitución 1 + x4 = x4 t2 , de aquí obtenemos x = 2 (t − 1)1/4 tdt dx = − 2 . Luego 2(t − 1)5/4 Z Z Z 1 dx −11 4 −1/2 √ (t2 − 1)2 dt dx = x (1 + x ) dx = − 2 x11 1 + x4 Z t5 t3 t 1 = − + − +C =− (t4 − 2t2 + 1)dt 10 3 2 2 1 p 1 p 1 √ 4 )5 + 4 )3 − = − (1 + x (1 + x 1 + x2 + C. 10x10 3x6 2x2 CAPÍTULO 2 MISCELÁNEA DE INTEGRALES Las siguientes integrales son una recopilación de exámenes hechos en la facultades de ciencias e ingeniería de la Universidad de Los Andes, y están presentados con la intención de que el lector desarrolle los métodos de integración presentados previamente. Se recomienda hacerlos antes y luego comparar los resultados. 2.1. Ejercicios Propuestos x2 √ dx 3 x3 − 1 1. Z 2. Z 3. Z earctan x + x ln(1 + x2 ) + 1 dx 1 + x2 4. Z dx √ ex 5. Z 6. Z dx q √ (1 + x2 ) ln(x + 1 + x2 ) 7. Z 8. Z x √ dx 1 − x4 dx √ √ x+1− x 2 x arctan(3x)dx 2 x arcsenxdx 9. Z √ sen xdx 10. Z √ arc cos( 1 − x)dx 11. Z arcsen r 12. Z e−x ln(ex + 1)dx 13. Z x3 ex dx 14. Z arc cos2 xdx 15. Z earcsenx dx 16. Z x arctan x √ dx 1 + x2 x x+1 2 dx 60 2.1. Ejercicios Propuestos 17. Z x2 arctan x dx 1 + x2 18. Z ln(x2 + x)dx 19. Z ln x √ dx 1−x 20. Z √ 21. Z arctan xdx Z x+1 dx x2 + 3 22. √ 2 x xe dx √ Z arctan x dx x2 Z √ 25. Z x arctan x √ dx 1 + x2 26. Z x5 27. Z ex + 1 dx e2x − 9 28. Z e2x dx e4x + 5 29. Z dx 4senx + 3 cos x + 5 30. Z dx senx − cos x + 2 31. Z x4 − 6x dx x4 − 16 32. Z dx (1 + x2 )3 33. Z dx 1 + x4 23. 24. 34. Z √ 35. Z (cos2 x)(sen5 x)dx 36. Z cos6 (2x)sen2 (2x)dx 37. Z (tan5 x)(sec7 x)dx 38. Z (tan4 x)(sec6 x)dx 39. Z 40. Z 41. Z 42. Z ex + 1dx dx − x2 tan xdx x (tan2 x)(cos2 x) dx, sin usar tan tan x + 1 2 dx p (x2 − 2x + 5)3 √ x x2 + 2x + 2 dx √ x3 dx 64 − x2 43. Z √ 44. Z (x + 45. Z dx √ x4 1 + x2 46. Z √ 47. Z √ 48. Z x2/3 (x5/3 + 1)2/3 dx 49. Z 2x3 dx (x2 + 1)2 50. Z sen2 (2x)sen2 xdx 51. Z x2 − 6x − 7 dx 1)2 dx √ x2 + 2x + 2 dx x2 − 2x − 3 x2 dx x6 − 1 dx √ (x − 1) x2 − 1 61 2. Miscelánea de integrales 52. Z √ 1+ e−2x dx dx 53. (senx)(2 cos2 x − 1) √ Z 8 x √ √ 54. dx x+2 4x+1 Z dx √ 55. 3 x 1 + x4 Z dx 56. 2 sen x cos4 x Z √ x32+x √ dx x+ 32+x 57. Z 58. Z 59. Z 60. Z ln(2x) 1 dx ln(4x) x 61. Z x cos4 xdx xarcsenx p dx (1 − x2 )3 xex dx (x + 1)2 62 2.2. Solución de los Ejercicios Propuestos 2.2. 1. Solución de los Ejercicios Propuestos Z x2 √ dx. 3 x3 − 1 Llamemos t = x3 − 1, de donde obtenemos dt = 3x2 dx, así Z 2. Z √ x2 1 √ dx = 3 3 3 x −1 Z dt 1 √ = 3 3 t Z x √ dx = 1 − x4 Z t−1/3 dt = 1√ 1p 3 t2 + C = 3 (x3 − 1)2 + C. 2 2 x dx. 1 − x4 Notemos que Z x p 1 − (x2 )2 dx. Llamemos t = x2 , de donde obtenemos dt = 2xdx, así Z 3. Z x √ dx = 1 − x4 Z 1 p dx = 2 1 − (x2 )2 x Z √ dt 1 1 = arcsent + C = arcsenx2 + C. 2 2 2 1−t earctan x + x ln(1 + x2 ) + 1 dx 1 + x2 Notemos que Z Z Z Z arctan x xdx dx e + x ln(1 + x2 ) + 1 arctan x dx 2 dx = e + ln(1 + x ) + . 2 2 2 1+x 1+x 1+x 1 + x2 dx dx , y llamemos t = arctan x. De esta forma dt = . 1 + x2 1 + x2 Luego Z Z arctan x dx I1 = e = et dt = et + C = earctan x + C. 1 + x2 Z xdx . Por otro lado sea I2 = ln(1 + x2 ) 1 + x2 2xdx . Así y llamemos t = ln(1 + x2 ), de donde obtenemos dt = 1 + x2 Z Z 1 2 xdx 1 1 2 2 tdt = I2 = ln(1 + x ) = t + C = ln (1 + x2 ) + C. 1 + x2 2 4 4 Consideremos así I1 = Z earctan x 63 2. Miscelánea de integrales Ahora bien, consideremos I3 = Z dx = arctan x + C. 1 + x2 Por último tenemos Z arctan x e + x ln(1 + x2 ) + 1 1 dx = I1 + I2 + I3 = earctan x + ln2 (1 + x2 ) + arctan x + C. 2 1+x 4 4. dx √ ex Z Z 5. Z dx √ = ex Z dx = x (e )1/2 dx q (1 + x2 ) ln(x + Llamemos t = ln(x + Z 6. √ 7. √ √ q = 1 + x2 ) Z q 1 dx . ·√ √ 2 1 + x 2 ln(x + 1 + x ) 1 + x2 ), de donde obtenemos dt = √ dx (1 + x2 ) ln(x + dx √ x+1− x Z Z 2 e−1/2x dx = −2e−1/2x + C = −2(ex )−1/2 + C = − √ x + C. e dx q √ (1 + x2 ) ln(x + 1 + x2 ) Notemos que Z Z Z √ dx . Así 1 + x2 dx 1 ·√ √ 1 + x2 1 + x2 ) ln(x + 1 + x2 ) Z Z √ 1 1 √ dt = t− 2 dt = 2 t + C = q t √ = 2 ln(x + 1 + x2 ) + C. = Z q √ Z Z Z √ √ √ x+1+ x dx √ dx = x + 1 dx + x dx √ = x+1− x Z (x − 1) − x Z 2p 2√ 3 = (x + 1)1/2 dx = x1/2 dx = (x + 1)3 + x + C. 3 3 x2 arctan(3x)dx. 64 2.2. Solución de los Ejercicios Propuestos Tomemos 3 dx 1 + 9x2 u = arctan(3x) −→ du = dv = x2 dx −→ v = Así Z x3 x arctan(3x)dx = arctan(3x) − 3 8. x3 3 · dx 3 1 + 9x2 Z 2 x3 = arctan(3x) − 3 x3 dx 1 + 9x2 Z x3 1 x = arctan(3x) − x− dx 3 9 1 + 9x2 Z Z x3 1 1 xdx = arctan(3x) − xdx + 3 9 9 1 + 9x2 Z x3 18x 1 2 1 = arctan(3x) − x + dx 3 18 162 1 + 9x2 = arctan(3x) Z x3 , 3 Z x3 1 1 − x2 + ln(1 + 9x2 ) + C. 3 18 162 x2 arcsenxdx. Tomemos u = arcsenx −→ du = √ dv = x2 dx −→ v = Así Z x3 3 1 x3 x arcsenxdx = arcsenx − 3 3 2 1 dx 1 − x2 Z √ x3 dx 1 − x2 x3 dx haciendo un cambio de variable. Llamemos x = sent, 1 − x2 de donde obtenemos dx = cos tdt. Así Ahora calculemos Z Z √ x3 √ dx = 1 − x2 = Z Z (sen3 t)(cos t) √ dt = 1 − sen2 t 2 Z (1 − cos t)sentdt = 3 sen tdt = Z sentdt − Z Z √ cos3 t + C = − 1 − x2 + = − cos t + 3 y finalmente (sen2 t)(sent)dt (cos2 t)(sent)dt p (1 − x2 )3 + C, 3 65 2. Miscelánea de integrales Z 1 x3 arctan x − x arcsenxdx = = 3 3 2 = 9. Z 1 x3 arctan x − 3 3 x3 dx 1 − x2 ! p 2 )3 √ (1 − x − 1 − x2 + + C. 3 Z √ √ sen xdx. Llamemos x = t2 , de donde obtenemos dx = 2tdt. Así Z Z Z √ sen xdx = (sent)2tdt = 2 tsentdt. Ahora aplicamos integración por partes a Z 10. tsentdt, para ello consideremos lo siguiente: u = t −→ du = dt dv = sentdt −→ v = − cos t Así Z Z √ sen xdx = 2 Z Z tsentdt = 2 −t cos t + cos tdt = −2t cos t + sent + C √ √ √ = −2 x cos x + sen x + C. √ arc cos( 1 − x)dx. √ √ Llamemos arc cos( 1 − x) = t, de donde 1 − x = cos t y de aquí obtenemos 1 − √ dx = −sentdt, 2 1−x √ luego dx = 2 1 − xsentdt = 2(cos t)(sent)dt = sen(2t)dt, y así Z Z √ arc cos( 1 − x)dx = t sen(2t)dt. Ahora aplicamos integración por partes a Tomemos así Z t sen(2t)dt. u = t −→ du = dt dv = sen(2t)dt −→ v = − cos(2t) , 2 66 2.2. Solución de los Ejercicios Propuestos De esta manera Z Z Z √ cos(2t) 1 cos(2t)dt + arc cos( 1 − x)dx = tsen(2t)dt = −t 2 2 = −t cos(2t) 1 + sen(2t) + C 2 4 cos2 t − sen2 t 1 = −t + 2(sent)(cos t) + C, 2 4 √ √ √ 2 y como cos t = 1 − x tenemos sent = 1 − cos t = x. Finalmente √ cos2 t − sen2 t 1 + (sent)(cos t) + C arc cos( 1 − x)dx = = −t 2 2 √ √ √ 1√ √ = − arc cos( 1 − x)[( 1 − x)2 − ( x)2 ] + x 1−x+C 2 √ 1p x(1 − x) + C. = − arc cos( 1 − x)(1 − 2x) + 2 r Z x 11. arcsen dx. x+1 Z Tomemos u = arcsen r x x+1 1 −→ du = √ dx 2 x(x + 1) dv = dx −→ v = x, Así Z arcsen r x x+1 dx = = arcsen r x x+1 1 x− 2 Z x 1 √ dx. (x + 1) x 1 √ dx haciendo un cambio de variable. Llamemos x = t2 , (x + 1) x de donde obtenemos dx = 2tdt. De esta manera Z Z Z Z 1 1 t2 t2 √ dx = x dt 2tdt = 2 dt = 2 1− 2 (t2 + 1)t t2 + 1 t +1 (x + 1) x Z Z 1 = 2 dt − 2 dt = 2t − 2 arctan t + C t2 + 1 √ √ = 2 x − 2 arctan x + C. Ahora calculemos Z x Finalmente r r Z Z x x 1 1 √ dx dx = arcsen x− x arcsen x+1 x+1 2 (x + 1) x r √ √ x x − x + arctan x + C. = arcsen x+1 67 2. Miscelánea de integrales 12. Z e−x ln(ex + 1)dx. Tomemos u = ln(ex + 1) −→ du = ex dx ex + 1 dv = e−x dx −→ v = −e−x , Luego Z −x e x −x ln(e + 1)dx = −e −x = −e −x = −e x ln(e + 1) − x ln(e + 1) + x ln(e + 1) + Z Z Z (−e−x )ex dx ex + 1 1 dx ex + 1 ex dx ex (ex + 1) ex haciendo un cambio de variable. Llamemos ex = t, de ex (ex + 1) donde obtenemos ex dx = dt, y así Z Z Z Z dt dt dt ex = = A + B ex (ex + 1) t(t + 1) t t+1 Ahora calculemos Z = A ln |t| + B ln |t + 1| + C = A ln |ex | + B ln |ex + 1| + C = Ax + B ln(ex + 1) + C. Observemos que: 1 A B = + , t(t + 1) t t+1 y calculando los coeficientes tenemos: A = 1 y B = −1. Finalmente Z Z ex −x x −x x e ln(e + 1)dx = −e ln(e + 1) + dx ex (ex + 1) = −e−x ln(ex + 1) + Ax + B ln(ex + 1) + C = −e−x ln(ex + 1) + x − ln(ex + 1) + C. 13. Z 3 x2 x e dx = Z 2 x2 ex xdx. Llamemos t = x2 , de donde obtenemos dt = 2xdx. De esta forma Z Z Z 1 3 x2 2 x2 tet dt. x e dx = x e xdx = 2 68 2.2. Solución de los Ejercicios Propuestos Ahora aplicamos integración por partes a Z tet dt. Para ello tomemos u = t −→ du = dt dv = et dt −→ v = et , De esta manera Z Z Z 1 1 1 1 1 2 3 x2 t t t x e dx = te dt = te − e dt = tet − et + C = ex (x2 − 1) + C. 2 2 2 2 2 14. Z arc cos2 xdx. Llamemos t = arc cos x, de donde cos t = x y de aquí −sentdt = dx. Así Z Z 2 arc cos xdx = − t2 sentdt. Aplicamos integración por partes a Z t2 sentdt. u = t2 −→ du = 2tdt dv = sentdt −→ v = − cos t, Z Z 2 2 2 arc cos xdx = − t sentdt = t cos t − 2 (cos t)tdt Z Ahora aplicamos integración por partes a (cos t)tdt. Para ello consideremos Z u = t −→ du = dt dv = cos tdt −→ v = sent. Finalmente tenemos: Z Z Z 2 2 2 arc cos xdx = t cos t − 2 (cos t)tdt = t cos t − 2 tsent − sentdt = t2 cos t − 2tsent − 2 cos t + C √ = (arc cos2 x)x − 2(arc cos x) 1 − x2 − 2x + C. 15. Z earcsenx dx. Llamemos t = arcsenx, de donde sent = x y de aquí cos tdt = dx. Así Z Z arcsenx e dx = et cos tdt. 69 2. Miscelánea de integrales Apliquemos integración por partes a Z et cos tdt. Tomemos u = cos t −→ du = −sentdt dv = et dt −→ v = et , Así Z t t e cos tdt = e cos t + Ahora apliquemos integración por partes a Z Z et sentdt. et sentdt. Tomemos u = sent −→ du = cos tdt dv = et dt −→ v = et Así Z t t e cos tdt = e cos t + Z Z t t e sentdt = e cos t + e sent − e cos tdt t t Observemos que después de aplicar el método llegamos a la integral inicial, entonces tratamos la expresión como una ecuación. Z 16. Z earcsenx dx = Z √ t ( 1 + x2 + x)earcsenx (cos t + sent)e +C = + C. et cos tdt = 2 2 x arctan x √ dx. 1 + x2 Llamemos t = arctan x, de donde tan t = x y de aquí obtenemos sec2 tdt = dx, así Z x arctan x √ dx = 1 + x2 Z √ t tan t 2 1 + tan2 t sec tdt = Ahora aplicamos integración por partes a Z Z t(tan t)(sec2 t) dt = sec t Z t(tan t)(sec t)dt. t(tan t)(sec t)dt. u = t −→ du = dt dv = (tan t)(sec t)dt −→ v = sec t, Z x arctan x √ dx = 1 + x2 Z t(tan t)(sec t)dt = t sec t − Z = = t sec t − ln | sec t + tan t| + C sec tdt √ √ = = (arctan x) 1 + x2 − ln | 1 + x2 + x| + C. 70 17. 2.2. Solución de los Ejercicios Propuestos Z x2 arctan x dx. 1 + x2 Notemos que Z x2 arctan x dx = 1 + x2 Z x2 arctan x 1 dx. 1 + x2 1 dx, y así Llamemos t = arctan x de donde tan t = x y de aquí obtenemos dt = 1 + x2 Z Z Z Z 2 x arctan x 1 2 2 dx = x arctan x dx = (tan t)tdt = (sec2 t − 1)tdt. 1 + x2 1 + x2 Z Z Z t2 2 = t sec tdt − tdt = t sec2 tdt − + C. 2 Z Ahora aplicamos integración por partes a t sec2 tdt. u = t −→ du = dt dv = sec2 tdt −→ v = tan t, Por lo tanto Z 2 Z Z x arctan x t2 t2 2 dx = t sec tdt − + C = t tan t − tan tdt − +C 1 + x2 2 2 t2 = = t tan t + ln | cos t| − + C 2 arctan2 x 1 √ + C. = x arctan x + ln − 2 1 + x2 18. Z ln(x2 + x)dx. Tomemos 2x + 1 dx x2 + x dv = dx −→ v = x, Z Z Z x(2x + 1) 2x + 1 2 2 2 ln(x + x)dx = ln(x + x)x − dx = ln(x + x)x − dx 2 x Z x + x Z+1 Z 1 dx 2 2 = ln(x + x)x − 2− dx = ln(x + x)x − 2dx + x+1 x+1 = x ln(x2 + x) − 2x + ln |x + 1| + C. Z ln x √ 19. dx 1−x u = ln(x2 + x) −→ du = Llamemos 1 − x = t2 , de donde x = 1 − t2 y de aquí obtenemos dx = −2tdt, y así 71 2. Miscelánea de integrales Z ln(1 − t2 ) tdt = −2 ln(1 − t2 )dt t Z Ahora aplicamos integración por partes a ln(1 − t2 )dt. Tomemos Z ln x √ dx = −2 1−x Z u = ln(1 − t2 )dt −→ du = dv = dt −→ v = t −2t 1 − t2 Así ln x √ dx = −2 1−x Z Z Z 2 ln(1 − t )dt = −2 t ln(1 − t ) + 2 2 t2 dt 1 − t2 Z 1 2 dt = −2t ln(1 − t ) − 4 −1 + 1 − t2 Z 1 2 = −2t ln(1 − t ) + 4t − 4 dt 1 − t2 2 = −2t ln(1 − t ) − 4 Z t2 dt 1 − t2 Observemos que: 1 A B = + , 1 − t2 1−t 1+t 1 1 y calculando los coeficientes tenemos: A = y B = − . Finalmente 2 2 Z Z 1 ln x √ dx = −2t ln(1 − t2 ) + 4t − 4 dt 1 − t2 1−x = −2t ln |1 − t2 | + 4t + 4A ln |1 − t| − 4B ln |1 + t| + C √ √ √ √ = −2 1 − x ln |x| + 4 1 − x + 2 ln |1 − 1 − x| − 2 ln |1 + 1 − x| + C. 20. Z √ √ x e2 x dx. Llamemos x = t2 de Z Z donde obtenemos dx = 2tdt. De esta manera √ 2√x x e dx = 2 t2 e2t dt. Z Aplicamos integración por partes a t2 e2t dt. u = t2 −→ du = 2tdt dv = e2t dt −→ v = e2t , 2 72 2.2. Solución de los Ejercicios Propuestos Luego Z √ Tomemos así √ 2 x xe dx = 2 Z 2t Z Z 2e 2t 2 2t t e dt = 2 t − e tdt = t e − 2 e2t tdt 2 2 2t u = t −→ du = dt e2t dv = e2t dt −→ v = , 2 Z Z √ 2√x 2 2t x e dx = t e − 2 e2t tdt 2t Z e 1 2t e dt = t e −2 t − 2 2 e2t 1 2 2t 2t 2 2t = t e − te − t −t− +C +C =e 2 2 √ √ 1 2 x + C. x− x− = e 2 2 2t 21. Z √ arctan xdx. Llamemos x = t2 , de donde obtenemos dx = 2tdt, y así Z Z Z √ arctan xdx = (arctan t)2tdt = 2 (arctan t)tdt. Ahora aplicamos integración por partes a Z (arctan t)tdt. u = arctan t −→ du = dv = tdt −→ v = Así Z arctan √ xdx = = = = dt 1 + t2 t2 2 Z t2 t2 1 2 (arctan t)tdt = 2 (arctan t) − dt 2 2 1 + t2 Z 1 2 dt (arctan t)t − 1− 1 + t2 Z Z dt 2 = t2 arctan t − t + arctan t + C (arctan t)t − dt + 1 + t2 √ √ √ x arctan x − x + arctan x + C. Z 73 2. Miscelánea de integrales 22. Z x+1 dx x2 + 3 √ Z Z Z x+1 3 1 xdx dx x 2 dx = + = ln |x + 3| + arctan √ + C. x2 + 3 x2 + 3 x2 + 3 2 3 3 23. Z arctan x dx. x2 Llamemos t = arctan x, de donde tan t = x y de aquí obtenemos sec2 tdt = dx, y así Z Z Z t arctan x 2 dx = sec tdt = t(tan−2 t)(sec2 t)dt. x2 tan2 t Ahora aplicamos integración por partes a Z t(tan−2 t)(sec2 t)dt. u = t −→ du = dt 1 1 (sec2 t)dt −→ v = − dv = 2 tan t tan t De esta manera Z arctan x t dx = − + 2 x tan t 24. 1 t tan Z t = − t + cot tdt tan t t + ln |sent| + C = − tan t = − Z Z √ √ 1 + x2 x 1 2 arctan t x + ln √ +C t 1 + x2 ex + 1dx. Llamemos t2 = ex + 1, de donde 2tdt = ex dx = (t2 − 1)dx y de aquí obtenemos 2tdt dx = 2 , y así t −1 Z Z Z Z √ 2tdt t2 1 x e + 1 dx = t 2 dt =2 dt = 2 1+ 2 t −1 t2 − 1 t −1 Z Z Z Z dt dt dt = 2t + 2A + 2B . = 2 dt + 2 t2 − 1 t−1 t+1 Observemos que: t2 A B 1 = + , −1 t−1 t+1 74 2.2. Solución de los Ejercicios Propuestos y calculando los coeficientes tenemos: A = √ Z 25. Z ex dt + 2B t−1 1 1 y B = − . Finalmente 2 2 Z dt dt + 1 dx = 2t + 2A − t−1 t+1 √ √ ex + 1 − 1 = 2t + ln |t − 1| − ln |t + 1| + C = 2 ex + 1 + ln √ x + C. e +1+1 Z Z dt = 2t + t+1 Z x arctan x √ dx. 1 + x2 Llamemos t = arctan x, de donde tan t = x y de aquí obtenemos sec2 tdt = dx, y así x arctan x √ dx = 1 + x2 Z Z (tan t)t(sec2 t) √ dt = 1 + tan2 t Ahora aplicamos integración por partes a Z Z t(sec2 t)(tan t) dt = sec t Z t(sec t)(tan t)dt. t(sec t)(tan t)dt. Tomemos así u = t −→ du = dt dv = (sec t)(tan t)dt −→ v = sec t Así Z x arctan x √ dx = 1 + x2 Z t(sec t)(tan t)dt = t sec t − Z sec tdt = t sec t − ln | sec t + tan t| + C √ √ = x 1 + x2 − ln | 1 + x2 + x| + C. 26. Z x5 dx − x2 Z dx = 5 x − x2 Z dx = 2 x (x3 − 1) Z x2 (x dx . − 1)(x2 + x + 1) Observemos que: x2 (x 1 A B D Ex + F = + + 2+ 2 2 − 1)(x + x + 1) x−1 x x x +x+1 2. Miscelánea de integrales 75 Así Z dx = 5 x − x2 dx − 1)(x2 + x + 1) Z Z Z Z Z dx dx dx xdx dx = A +B +D + E + F x−1 x x2 x2 + x + 1 x2 + x + 1 Z Z D E 2x + 2 dx E = A ln |x − 1| + B ln |x| − + dx − 2 x 2 x +x+1 2 (x + 21 )2 + 43 Z dx +F (x + 12 )2 + 43 Z x2 (x D E + ln |x2 + x + 1| x 2 √ 2 3 2x E arctan √ + C, − +F 2 3 3 = A ln |x − 1| + B ln |x| − 1 y calculando los coeficientes tenemos: A = , D = −1, . . . 3 27. Z ex + 1 dx. e2x − 9 dt , así t Z Z Z Z Z x t + 1 dt dt dt dt e +1 dx = =A +B +D 2x 2 e −9 (t − 9) t t t−3 t+3 Llamemos t = ex , de donde dt = ex dx y de aquí obtenemos dx = = A ln |t| + B ln |t − 3| + D ln |t + 3| + C = A ln |ex | + B ln |ex − 3| + D ln |ex + 3| + C = Ax + B ln |ex − 3| + D ln |ex + 3| + C, 1 2 1 y calculando los coeficientes tenemos: A = − , B = y D = . 9 9 9 28. Z e2x dx. e4x + 5 Llamemos t = e2x , de donde dt = 2e2x dx, así Z 1 e2x dx = 4x e +5 2 Z √ √ 2x dt 1 5 t e 5 = arctan √ arctan √ +C = + C. 2 t +5 2 5 10 5 5 76 29. 2.2. Solución de los Ejercicios Propuestos Z dx 4senx + 3 cos x + 5 Z 2dt Z 2 dx dt 1 + t = =2 2 2 2t 4senx + 3 cos x + 5 2t + 8t + 8 1−t 4 +3 +5 2 2 1+ Zt Z 1+t 1 dt dt = =− +C = 2 2 t + 4t + 4 (t + 2) 3(t + 2)3 Z 1 i + C. x = − h +2 3 tan 2 30. Z dx senx − cos x + 2 Z dx = senx − cos x + 2 = = = 31. 2dt Z dt 1 + t2 =2 2 2 2t 3t + 2t + 1 1−t − +2 2 2 1+t Z1 + t Z dt dt 2 2 = 1 2 2 3 3 t2 + 3 t + 3 (t + 3 )2 + 92 √ t + 13 2 3 2 · arctan √ +C 3 2 2 ! √ 3 tan( x2 ) + 31 √ + C. 2 arctan 2 Z x4 − 6x dx x4 − 16 Notemos que Z 4 Z Z Z Z x − 6x 16 − 6x 16 − 6x 8 − 3x dx = dx + dx = 1+ 4 dx = x + 2 dx. 4 4 x − 16 x − 16 x − 16 x4 − 16 Z 8 − 3x dx. Ahora calculemos la integral x4 − 16 Z Z 8 − 3x 8 − 3x dx = dx 2 2 (x − 4)(x + 4) (x − 2)(x + 2)(x2 + 4) Z Z Z Z dx dx x dx = A +B +D dx + E 2 2 x−2 x+2 x +4 x +4 x D E = A ln |x − 2| + B ln |x + 2| + ln |x2 + 4| + arctan + C, 2 2 2 1 7 2 11 donde A = , B = , D = y E = − . Finalmente 16 16 3 4 Z 8 − 3x dx = x4 − 16 Z 77 2. Miscelánea de integrales Z x4 − 6x dx = x + 2 x4 − 16 = x+ 32. Z dx = (1 + x2 )3 Z Z 8 − 3x dx x4 − 16 x 1 11 7 2 + C. ln |x − 2| + ln |x + 2| + ln x2 + 4 − arctan 8 8 3 4 2 1 dx . 2 2 (1 + x ) (1 + x2 ) Llamemos x = tan t, de donde arctan x = t y de aquí obtenemos dt = Z 33. Z dx = (1 + x2 )3 dx . Así 1 + x2 Z Z Z 1 1 dt dx = dt = = cos4 tdt (1 + x2 )2 (1 + x2 ) (1 + tan2 t)2 sec4 t 2 Z Z 1 + cos(2t) 1 [1 + 2 cos(2t) + cos2 (2t)]dt = dt = 2 4 Z Z Z 1 1 1 + cos(4t) 1 dt + cos(2t)dt + dt = 4 2 4 2 Z = 1 1 sen(2t) 1 1 sen(4t) t+ + t+ +C 4 2 2 8 8 4 = 1 1 1 1 arctan x + sen(2 arctan x) + arctan x + sen(4 arctan x) + C. 4 4 8 32 dx 1 + x4 Notemos que Z dx = 1 + x4 = Z Z dx = x4 − 2x2 + 2x2 + 1 (x2 + 1 − √ Z dx (x2 + 1)2 − 2x2 dx √ . 2x)(x2 + 1 + 2x) Por otro lado: (x2 − √ Ax + B Dx + E 1 √ √ √ = + 2 2 2 2x + 1)(x + 2x + 1) x − 2x + 1 x + 2x + 1 78 2.2. Solución de los Ejercicios Propuestos De esta forma Z Z Z dx dx xdx √ √ √ = =A 4 1+x (x2 + 1 − 2x)(x2 + 1 + 2x) x2 − 2x + 1 Z Z Z dx xdx dx √ √ √ +B +D +E 2 2 2 x − 2x + 1 x + 2x + 1 x + 2x + 1 √ √ √ √ Z Z Z 2x − 2 + 2 x− 2+ 2 dx A √ √ +D dx + B dx = √ 2 2 + 2 x2 − 2x + 1 x 2x + 1 2 1 x− 2 +2 Z dx +E √ 2 x + 22 + 21 √ Z Z Z A 2x − 2 A√ dx dx √ = +B dx + 2 2 √ √ 2 2 2 x2 − 2x + 1 1 2 2 x− 2 x− 2 +2 + 21 √ Z Z Z √ dx dx x+ 2 √ +E +D dx − D 2 2 √ √ 2 x2 + 2x + 1 x + 22 + 21 x + 22 + 12 √ ! 2 √ √ √ x − A 2 √ = ln |x2 − 2x + 1| + ( 2A + B) 2 arctan 2 2 2 √ ! 2 √ √ √ x + D 2 2 √ + C, + ln |x + 2x + 1| + (E + D 2) 2 arctan 2 2 2 donde los valores de A, B, D y E se encuentran aplicando el método de los coeficientes indeterminados. √ √ Sugerencia: Dar a x los valores 0, 1, 2 y − 2 sucesivamente. Z √ 34. tan x dx. Llamemos t2 = tan x, de donde 2tdt = (tan2 x + 1)dx = (t4 + 1)dx y de aquí obtenemos 2tdt . Así dx = 1 + t4 Z Z Z √ √ t2 2t 2 dt = 2 dt, tan x dx = t 1 + t4 1 + t4 y esto se reduce a calcular la integral anterior. 79 2. Miscelánea de integrales 35. Z (cos2 x)(sen5 x)dx Z 2 5 (cos x)(sen x)dx = = = Z Z Z = − 36. Z 2 4 (cos x)(sen x)(senx)dx = Z (cos2 x)(1 − cos2 x)2 (senx)dx (cos2 x)(1 − 2 cos2 x + cos4 x)(senx)dx 2 (cos x)(senx)dx − 2 Z 4 (cos x)(senx)dx + cos5 x cos7 x cos3 x +2 − + C. 3 5 7 Z (cos6 x)(senx)dx cos6 (2x)sen2 (2x)dx Z Z 6 2 cos (2x)sen (2x)dx = cos4 (2x)sen2 (2x) cos2 (2x)dx sen2 (4x) dx 4 2 Z 1 − cos(4x) 1 = sen2 (4x)dx 4 2 Z 1 [1 − 2 cos(4x) + cos2 (4x)]sen2 (4x)dx = 16 Z Z 1 1 2 sen (4x)dx − sen2 (4x) cos(4x)dx = 16 8 Z 1 + sen2 (4x) cos2 (4x)dx 16 Z Z 1 1 − cos(8x) sen2 (8x) 1 sen3 (4x) 1 = dx − · + dx 16 2 8 3·4 16 4 Z Z 1 1 1 dx − cos(8x)dx − sen3 (4x) = 32 32 96 Z 1 1 − cos(16x) + dx 64 2 = Z [cos2 (2x)]2 x 1 sen(8x) sen3 (4x) x 1 sen(16x) = − − + − + C. 32 32 8 96 128 128 16 80 37. 2.2. Solución de los Ejercicios Propuestos Z (tan5 x)(sec7 x)dx Z 5 7 (tan x)(sec x)dx = = = = Z Z Z Z + = 38. Z (tan4 x)(sec6 x)(sec x)(tan x)dx (sec2 x − 1)2 (sec6 x)(sec x)(tan x)dx (sec4 x − 2 sec2 x + 1)(sec6 x)(sec x)(tan x)dx 10 (sec x)(sec x)(tan x)dx − 2 Z (sec6 x)(sec x)(tan x)dx sec11 x sec9 x sec7 x −2 + + C. 11 9 7 4 6 (tan x)(sec x)dx = = = = Z Z Z Z + = 39. (sec8 x)(sec x)(tan x)dx (tan4 x)(sec6 x)dx Z Z Z (tan4 x)(sec4 x)(sec2 x)dx (tan4 x)(tan2 x + 1)2 (sec2 x)dx (tan4 x)(tan4 x + 2 tan2 x + 1)(sec2 x)dx 8 2 (tan x)(sec x)dx + 2 Z Z (tan6 x)(sec2 x)dx (tan4 x)(sec2 x)dx tan9 x tan7 x sec5 x +2 + + C. 9 7 5 (tan2 x)(cos2 x) dx tan x + 1 Notemos que Z (tan2 x)(cos2 x) dx = tan x + 1 Z = Z (tan2 x)(cos4 x) = (tan x + 1) cos2 x Z (tan2 x)(sec2 x) dx (tan x + 1) sec4 x (tan2 x)(sec2 x) dx. (tan x + 1)(1 + tan2 x)2 81 2. Miscelánea de integrales Llamemos t = tan x, de donde obtenemos dt = sec2 xdx, y así Z Z Z (tan2 x)(sec2 x) t2 dt (tan2 x)(cos2 x) dx = dx = . tan x + 1 (tan x + 1)(1 + tan2 x)2 (t + 1)(1 + t2 )2 Observemos que: t2 A Bt + D Et + F = + + , 2 2 2 (t + 1)(1 + t ) t+1 1+t (1 + t2 )2 1 1 1 1 1 y calculando los coeficientes tenemos: A = , B = − , D = , E = y F = − . Fi4 4 4 2 2 nalmente Z t2 dt (t + 1)(1 + t2 )2 Z Z Z 1 dt t−1 t−1 1 1 = − dt + dt 2 2 4 t+1 4 t +1 2 (t + 1)2 √ 1 1 1+t 1 2 ln |t + 1| − ln | t + 1| − +C = 4 4 4 1 + t2 (tan2 x)(cos2 x) dx = tan x + 1 = Z 1 1 ln |senx + cos x| − (cos x)(senx + cos x) + C. 4 4 Resolvamos este ejercicio de otra manera, para mostrar cómo el uso de las recurrencias algebraicas y/o trigonométricas pueden simplificar el cálculo de una integral. Z (tan2 x)(cos2 x) dx = tan x + 1 = = = = Z (sen2 x)(cos x) dx = senx + cos x Z (sen2 x)(cos x − senx)(cos x) dx cos2 −sen2 x Z (sen2 x)(cos2 x) (sen2 x)(senx)(cos x) dx − dx cos(2x) cos(2x) Z Z 1 sen2 (2x) (sen2 x)sen(2x) 1 dx − dx 4 cos(2x) 2 cos(2x) Z Z 1 − cos2 (2x) 1 − cos(2x) 1 1 dx − sen(2x)dx 4 cos(2x) 4 cos(2x) Z Z Z 1 1 1 sec(2x)dx − cos(2x)dx − tan(2x)dx 4 4 4 Z 1 sen(2x)dx + 4 Z = = 1 1 1 ln | sec(2x) + tan(2x)| − sen(2x) + ln | cos x| 4 8 4 1 − cos(2x) + C. 8 82 40. 2.2. Solución de los Ejercicios Propuestos dx p (x2 − 2x + 5)3 Z p Notemos que: Z dx dx , − 2x + [(x − 1)2 + 4]3 y haciendo el cambio de variable x − 1 = 2 tan t, se tiene que dx = 2 sec2 tdt. Luego Z Z Z dx dx 2 sec2 tdt p p p = = (x2 − 2x + 5)3 [(x − 1)2 + 4]3 (4 tan2 t + 4)3 Z Z sec2 t 1 2 sec2 tdt p p = dt = 32 (sec2 t)3 43 (tan2 t + 1)3 Z Z 1 sec2 t 1 1 cos tdt = dt = sent + C = 32 sec3 t 32 32 (x2 5)3 = Z p Por último cambiamos nuevamente a la variable original de la siguiente manera. x−1 Si x − 1 = 2 tan t, entonces tan t = y esto 2 nos sugiere la construcción del siguiente triángulo: x−1 t 2 x−1 . Finalmente Así sent = p (x − 1)2 + 4 Z 41. Z 1 1 dx p = sent + C = 32 32 (x2 − 2x + 5)3 x−1 p (x − 1)2 + 4 √ x x2 + 2x + 2 Notemos que Z p (x − 1)2 + 4 ! + C. Z p √ 2 x x + 2x + 2dx = x (x + 1)2 + 1 dx. Ahora bien, llamemos x + 1 = tan t, de donde x = tan t − 1, y de aquí obtenemos que dx = sec2 tdt. De esta forma Z √ Z p Z p x x2 + 2x + 2 dx = x (x + 1)2 + 1 dx = (tan t − 1) tan2 t + 1(sec2 t)dt = Z = Z 3 (tan t − 1)(sec t)dt = 2 Z (sec t)(sec t)(tan t)dt − Ahora aplicamos integración por partes a Z 3 (tan t)(sec t)dt − Z Z sec3 t − sec tdt = 3 3 sec3 tdt, para ello tomemos u = sec t −→ du = (sec t)(tan t)dt dv = sec2 t −→ v = tan t, sec3 tdt Z sec3 tdt. 83 2. Miscelánea de integrales De aquí se tiene que Z Z 3 sec tdt = (sec t)(tan t) − (tan2 t)(sec t)dt = (sec t)(tan t) − Z = (sec t)(tan t) − Z (sec2 t − 1)(sec t)dt 3 sec tdt + Z sec tdt Observemos que después de aplicar el método llegamos a la integral inicial, entonces tratamos la expresión como una ecuación. Z (sec t)(tan t) + ln | sec t + tan t| sec3 tdt = + C, 2 Así Z Z √ sec3 t 2 − sec3 tdt x x + 2x + 2dx = 3 = sec3 t (sec t)(tan t) + ln | sec t + tan t| − + C. 3 2 Por último cambiamos nuevamente a la variable original de la siguiente manera. Si x + 1 = tan t, entonces esto nos sugiere la construcción del siguiente triángulo: p (x + 1)2 + 1 x+1 t 1 Así sec t = Z p tan2 t + 1 = p (x + 1)2 + 1. Finalmente √ sec3 t (sec t)(tan t) + ln | sec t + tan t| x x2 + 2x + 2 dx = − + C. 3 2 p [(x + 1)2 + 1]3 = 3 p p (x + 1)2 + 1 (x + 1) + ln | (x + 1)2 + 1 + (x + 1)| − + C. 2 84 42. 2.2. Solución de los Ejercicios Propuestos Z √ x3 dx. 64 − x2 Hacemos el cambio de variable x = 8sent, de donde dx = 8 cos tdt. Así Z x3 √ dx = 64 − x2 Z Z 83 (sen3 t)(8 cos t) 3 √ dt = 512 sen tdt = 512 (sen2 t)(sent)dt 64 − 64sen2 t Z Z Z 2 = 512 (1 − cos t)(sent)dt = 512 sent − 512 (cos2 t)(sent)dt Z = 512 cos t − 512 cos3 t + C. 3 Por último cambiamos nuevamente a la variable original de la siguiente manera. x Si x = 8sent, entonces sent = y esto nos su8 giere la construcción del siguiente triángulo: Así cos t = Z 43. Z √ √ 8 x t p 64 − x2 64 − x2 . Finalmente 8 √ 3 64 − x2 √ x3 cos3 t 2 √ 64 − x + C512 − dx = = 512 cos t − 512 +C 3 8 64 − x2 p √ = 64 64 − x2 − (64 − x2 )3 + C. x2 − 6x − 7dx Observemos que Z √ x2 − 6x − 7dx = Z p (x − 3)2 − 16 dx. Así Hacemos el cambio de variable x − 3 = 4 sec t, de donde dx = 4(sec t)(tan t)dt. Así Z √ x2 Z p Z p 2 − 6x − 7 dx = (x − 3) − 16 dx = 4 (sec2 t − 1) 4(sec t)(tan t)dt = 16 = 16 Z Z (tan t)(sec t)(tan t)dt = 16 2 (sec t − 1)(sec t)dt = 16 Z Z (tan2 t)(sec t)dt 3 sec tdt − 16 Z sec tdt. 85 2. Miscelánea de integrales (sec t)(tan t) + ln | sec t + tan t| + C, así En el ejercicio 41 vimos que sec3 tdt = 2 Z √ Z Z 3 x2 − 6x − 7 dx = 16 sec tdt − 16 sec tdt Z = 16 (sec t)(tan t) + ln | sec t + tan t| − 16 ln | sec t + tan t| + C. 2 Por último cambiamos nuevamente a la variable x−3 p original de la siguiente manera. Si x − 3 = 4 sec t, (x − 3)2 − 16 x−3 entonces sec t = y esto nos sugiere la const 4 trucción del siguiente triángulo: 4 p (x − 3)2 − 16 . Finalmente Así tan t = 4 Z √ (sec t)(tan t) + ln | sec t + tan t| − 16 ln | sec t + tan t| + C x2 − 6x − 7 dx = 16 2 ! p p (x − 3)2 − 16 x−3 x − 3 (x − 3)2 − 16 + ln + = 8 4 4 4 4 p (x − 3)2 − 16 x−3 −16 ln +C + 4 4 p (x − 3)2 − 16 x − 3p x−3 2 + C. + = (x − 3) − 16 − 15 ln 2 4 4 44. Z (x + 1)2 dx √ x2 + 2x + 2 Obsérvese que Z dx √ = 2 (x + 1) x2 + 2x + 2 Z (x + 1)2 dx p . (x + 1)2 + 1 Hacemos el cambio de variable x + 1 = tan t, de donde obtenemos dx = sec2 tdt, y así Z Z Z dx sec2 tdt dx √ p √ = = (x + 1)2 x2 + 2x + 2 (x + 1)2 (x + 1)2 + 1 (tan t) tan2 t + 1 Z Z sec t dt = csc tdt = − ln | csc t + cot t| + C. = tan t Por último cambiamos nuevamente a la variable original de la siguiente manera. Si x + 1 = tan t, entonces esto nos sugiere la construcción del siguiente triángulo: p (x + 1)2 + 1 x+1 t 1 86 2.2. Solución de los Ejercicios Propuestos p (x + 1)2 + 1 . Finalmente Así, csc t = x+1 Z dx √ = − ln | csc t + cot t| + C (x + 1)2 x2 + 2x + 2 p (x + 1)2 + 1 1 + C. + − ln x+1 x+1 45. Z x4 dx √ . 1 + x2 Hacemos el cambio de variable x = tan t, de donde obtenemos dx = sec2 tdt, así Z Z Z Z cos3 t sec2 tdt dx sec t √ √ dt = dt = = tan4 t sen4 t x4 1 + x2 (tan4 t) 1 + tan2 t Z Z (cos2 t)(cos t) 1 − sen2 t = dt = cos tdt sen4 t sen4 t Z Z sen−3 t sen−1 t −4 = (sen t)(cos t)dt − (sen−2 t)(cos t)dt = − +C −3 −1 = − 1 1 1 + + C = − csc3 t + csc t + C. 3 3sen t sent 3 √ Por último cambiamos nuevamente a la variable x2 + 1 original de la siguiente manera. Si x = tan t, enx tonces esto nos sugiere la construcción del siguiente t triángulo: 1 √ 2 x +1 De esta manera, csc t = . Finalmente: x p √ Z dx 1 (x2 + 1)3 x2 + 1 1 3 √ + + C. = − csc t + csc t + C = − 3 3 x3 x x4 1 + x2 Z dx √ 46. x2 − 2x − 3 Notemos que Z dx √ = x2 − 2x − 3 Z dx p . (x − 1)2 − 4 Hacemos el cambio de variable x−1 = 2 sec t, de donde obtenemos dx = 2(sec t)(tan t)dt, así Z Z Z Z 2(sec t)(tan t)dt dx dx √ p √ = = = sec tdt x2 − 2x − 3 2 sec2 t − 1 (x − 1)2 − 4 = ln | sec t + tan t| + C. 87 2. Miscelánea de integrales Por último cambiamos nuevamente a la variable original de la siguiente manera. x−1 Si x − 1 = 2 sec t, entonces sec t = y esto 2 nos sugiere la construcción del siguiente triángulo: p (x − 1)2 − 4 Así, tan t = . Por lo tanto 2 Z 47. Z √ x−1 p (x − 1)2 − 4 t 2 dx x−1 √ = ln | sec t + tan t| + C = ln + 2 x2 − 2x − 3 p (x − 1)2 − 4 + C. 2 x2 dx x6 − 1 Obsérvese que Z x2 √ dx = x6 − 1 Z p x2 dx. (x3 )2 − 1 Llamemos t = x3 , de donde obtenemos dt = 3x2 dx, así Z x2 √ dx = x6 − 1 Z x2 1 p dx = 3 (x3 )2 − 1 Z √ dt . −1 t2 Ahora hacemos el cambio de variable t = sec z, de donde obtenemos dt = (sec z)(tan z)dz, y así Z Z Z dt (sec z)(tan z)dz (sec z)(tan z)dz x2 1 1 1 √ √ √ dx = = = 3 3 3 tan z x6 − 1 t2 − 1 sec2 z − 1 Z √ 1 1 1 sec zdz = ln | sec z + tan z| + C = ln |t + t2 − 1| + C = 3 3 3 √ 1 ln x3 + x6 − 1 + C. = 3 Z 48. Z 2/3 x 5/3 (x + 1) 2/3 dx = Z (x5/3 + 1)2/3 x2/3 dx. 5 Llamemos t = x5/3 , de donde obtenemos dt = x2/3 dx, así 3 Z Z Z 3 2/3 5/3 2/3 5/3 2/3 2/3 (t + 1)2/3 dt x (x + 1) dx = (x + 1) x dx = 5 = 3 (t + 1)5/3 9 + C = (x5/3 + 1)5/3 + C. 5 5/3 25 88 49. 2.2. Solución de los Ejercicios Propuestos Z 2x3 dx = (x2 + 1)2 Z x2 (2xdx) . (x2 + 1)2 Llamemos t − 1 = x2 , de donde t = x2 + 1 y de aquí obtenemos dt = 2xdx, así Z 2 Z Z Z Z x (2xdx) t−1 dt dt 1 2x3 dx = = dt = − = ln |t| + + C 2 2 2 2 2 2 (x + 1) (x + 1) t t t t = ln x2 + 1 + 50. Z 2 1 − cos(2x) dx 2 Z Z 1 1 2 sen (2x)dx − sen2 (2x) cos(2x)dx = 2 2 Z 1 1 − cos(4x) 1 sen3 (2x) = dx − +C 2 2 4 3 Z Z 1 1 1 dx − cos(4x)dx − sen3 (2x) + C = 4 4 12 2 sen (2x)sen xdx = = 51. 1 + C. +1 sen2 (2x)sen2 xdx Z Z x2 Z sen2 (2x) 1 1 1 x − sen(4x) − sen3 (2x) + C. 4 16 12 dx √ . (x − 1) x2 − 1 Hacemos el cambio de variable x−1 = sec t−1, de donde x = sec t y de aquí obtenemos dx = (sec t)(tan t)dt, así Z dx √ = (x − 1) x2 − 1 Z Z (sec t)(tan t)dt sec t 1 + cos t √ = dt = dt sec t − 1 1 − cos2 t (sec t − 1) sec2 t − 1 Z Z Z 1 + cos t 2 dt = csc tdt − (sen−2 t)(cos t)dt = sen2 t Z = − cot t − 1 + C. sent Por último cambiamos nuevamente a la variable original de la siguiente manera. Si x = sec t, entonces esto nos sugiere la construcción del siguiente triángulo: x √ x2 − 1 t 1 89 2. Miscelánea de integrales Así cot t = √ 52. Z √ 1 . Finalmente x2 −1 Z 1 dx 1 √ − cot t − + C = −√ − x + C. sent (x − 1) x2 − 1 x2 − 1 1 + e−2x dx Nótese que: Z √ 1+ e−2x Z r dx = Z √ = 1 1 + 2x dx = e Z r e2x + 1 dx = e2x Z √ e2x + 1 dx ex e2x + 1 x e dx. e2x Llamemos t = ex , de donde obtenemos dt = ex dx. Así Z √ 1+ e−2x dx = Z √ e2x + 1 x e dx = e2x Z √ t2 + 1 dt. t2 Ahora hacemos el cambio de variable t = tan z, de donde obtenemos dt = sec2 zdz, así Z √ 1+ e−2x dx = = = = = 53. Z Z √ Z sec z (sec2 z)(sec z) 2 sec zdz = dz tan2 z tan2 z Z Z Z (tan2 z + 1)(sec z) sec z dz = sec zdz + dz 2 tan z tan2 z Z cos z 1 ln | sec z + tan z| + dz = ln | sec z + tan z| − +C 2 sen z senz √ √ t2 + 1 2 ln t + 1 + t − +C t √ √ e2x + 1 x + C. ln e2x + 1 + e − ex t2 + 1 dt = t2 Z dx (senx)(2 cos2 x − 1) Notemos que Z dx = (senx)(2 cos2 x − 1) Z senxdx = 2 (sen x)(2 cos2 x − 1) Z (1 − senxdx . x)(2 cos2 x − 1) cos2 90 2.2. Solución de los Ejercicios Propuestos Llamemos t = cos x, de donde obtenemos dt = −senxdx, así Z Z Z senxdx dt dx = = 2 2 2 2 (senx)(2 cos x − 1) (1 − cos x)(2 cos x − 1) (t − 1)(2t2 − 1) Z dt = √ √ (t − 1)(t + 1)(2t − 2) t + 22 Z Z Z Z dt dt dt dt √ √ +E = A +B + t−1 t+1 2t − 2 t + 22 √ D = A ln |t − 1| + B ln |t + 1| + ln |2t − 2| 2 √ 2 +C +E ln t + 2 √ D = A ln | cos x − 1| + B ln | cos x + 1| + ln 2 cos x − 2 2 √ 2 + C, = +E ln cos x + 2 √ √ 1 1 y calculando los coeficientes tenemos: A = , B = , D = − 2 y E = 2. 2 2 54. Z √ 8 x √ √ dx x+2 4x+1 Sea t8 = x, de donde obtenemos dx = 8t7 dt, y así √ Z Z Z 8 x 8t8 t 7 √ √ 8t dt = dt dx = t4 + 2t2 + 1 t4 + 2t2 + 1 x+24x+1 Ahora bien, puesto que el grado del numerador es mayor que el denominador, al realizar la división de polinomios tenemos que 8t8 32t2 + 24 32t2 + 24 4 2 4 2 = 8t − 16t + 24 − = 8t − 16t + 24 − t4 + 2t2 + 1 t4 + 2t2 + 1 (t2 + 1)2 De esta forma aplicando el método de fracciones simples tenemos que √ Z Z 8 x 32t2 + 24 4 2 √ √ dt dx = 8t − 16t + 24 − 2 (t + 1)2 x+24x+1 Z Z Z Z 32t2 + 24 4 2 dt = 8 t dt − 16 t dt + 24 dt − (t2 + 1)2 Z Z Z Z Z B A 4 2 dt − dt = 8 t dt − 16 t dt + 24 dt − 2 2 t +1 (t + 1)2 91 2. Miscelánea de integrales B dt es la única no + 1)2 elemental. Calculemos dicha integral, para ello consideremos el cambio t = tan u, de donde dt = sec2 udu. Así Z Z Z Z B B B sec2 u B 2 dt = sec udu = du = du 2 2 2 2 4 (t + 1) (tan u + 1) sec u sec2 u Z Z Z Z 1 + cos(2u) B B 2 = B cos udu = B du = du + cos(2u)du 2 2 2 Notemos que muchas de esas integrales son elementales; Z (t2 (t2 = B B B B u + sen(2u) + C = u + senu cos u + C 2 4 2 4 = B B u + senu cos u + C 2 4 Por último cambiamos nuevamente a la variable original de la siguiente manera. Si t = tan u, entonces esto nos sugiere la construcción del siguiente triángulo: Así senu = √ Z √ 1 + t2 t u 1 t 1 y cos u = √ , y de esta forma 2 1+t 1 + t2 B B B B t t 1 B √ dt = arctan t + √ +C + C = arctan t + 2 2 2 + 1) 2 4 1+t 1+t 2 4 1 + t2 Finalmente √ √ Z 8 √ √ √ √ x B B 8x 8 4 8 √ √ √ +C arctan( x) − dx = 8 x − 16 x + 24 x − A + x+2 4x+1 2 4 1+ 4x donde, calculando los coeficientes, A = 32 y B = −8. Z dx √ 55. x3 1 + x4 Notemos que Z dx 1 √ = x−3 (1 + x4 )− 2 . 3 4 x 1+x 1 Además, m = −3, n = 4, p = − , a = 1 y b = 1. Así 2 Z m+1 −3 + 1 1 = = − , no es entero n 4 2 m+1 1 1 + p = − − = −1 es entero n 2 2 92 2.2. Solución de los Ejercicios Propuestos 1 De esta forma la sustitución es x−4 + 1 = z 2 , de donde obtenemos que x = (z 2 − 1)− 4 , z 5 y así dx = − (z 2 − 1)− 4 dz Por lo tanto 2 Z x3 dx √ = 1 + x4 = = = = = 5 − 1 1 1 z ((z 2 − 1)− 4 )−3 (1 + ((z 2 − 1)− 4 )4 )− 2 − (z 2 − 1) 4 dz 2 5 Z − 3 1 z (z 2 − 1) 4 (1 + (z 2 − 1)−1 )− 2 − (z 2 − 1) 4 dz 2 1 − 2 Z 1 1 2 − 21 zdz − (z − 1) 1+ 2 2 z −1 2 − 21 Z 1 1 z − zdz (z 2 − 1)− 2 2 2 z −1 Z 1 1 (z 2 )− 2 2 − 21 (z − 1) − 1 zdz 2 (z 2 − 1)− 2 Z 1 dz − 2 Z 1 = − z+C 2 De esta forma, regresando los cambios tenemos que Z dx 1 √ −4 1 √ x +1+C =− =− 2 2 x3 1 + x4 r √ x4 + 1 x4 + 1 + C = − +C x4 2x2 Otra forma de resolver esta integral es la siguiente: notemos que Z dx √ = 3 x 1 + x4 Z x4 √ x dx 1 + x4 Consideremos así el cambio x2 = tan t, teniéndose que 2xdx = sec2 t dt. De esta manera Z Z 1 sec2 t sec2 t √ √ dt = dt 2 tan2 t 1 + tan2 t tan2 t sec2 t Z Z Z sec2 t 1 sec t 1 cos t 1 dt = dt = 2 2 dt = 2 tan t sec t 2 tan t 2 sen2 t Z 1 sen−2 t cos t dt = 2 1 x √ dx = 4 4 2 x 1+x = − Z 1 +C 2sent 93 2. Miscelánea de integrales Cambiamos ahora a la variable original de la siguiente manera. Si x2 = tan t, entonces esto nos sugiere la construcción del siguiente triángulo: √ 1 + x4 x2 t 1 √ 1 + x4 x2 1 =− , y por lo Así sent = √ , obteniéndose de esto último que − 2sent 2x2 1 + x4 tanto √ Z dx 1 + x4 √ =− +C 2x2 x3 1 + x4 56. Z dx sen2 x cos4 x dx Notemos que Z dx dx = 2 sen x cos4 x Z = Z = Z = Z = Z Z sen2 x + cos2 x sen2 x cos2 x dx = dx + dx sen2 x cos4 x sen2 x cos4 x sen2 x cos4 x Z sin2 x + cos2 x 4 sec xdx + dx sen2 x cos2 x Z sen2 x + cos2 x 2 2 (1 + tan x) sec xdx + dx sen2 x cos2 x Z Z sen2 x cos2 x 2 2 (1 + tan x) sec xdx + dx + dx sen2 x cos2 x sen2 x cos2 x Z Z 2 2 2 (1 + tan x) sec xdx + sec xdx + csc2 xdx Z Consideremos así el cambio t = tan x, obteniéndose dt = sec2 xdx. De esta manera Z 2 2 (1 + tan x) sec xdx = Z 1 1 (1 + t2 )dt = t + t3 + C = tan x + tan3 x 3 3 Finalmente Z 57. Z √ x32+x √ dx x+ 32+x dx sen2 x cos4 x dx = 2 tan x + 1 tan3 x − cot x + C 3 94 2.2. Solución de los Ejercicios Propuestos Llamemos t3 = 2 + x, de donde x = t3 − 2 y por lo tanto dx = 3t2 dt. De esta manera Z √ Z (t3 − 2)t 2 x32+x √ dx = 3t dt t3 − 2 + t x+ 32+x 3t6 − 6t3 dt t3 + t − 2 = 3t6 − 6t3 dt (t − 1)(t2 + t + 2) = Al dividir y aplicar el método de fracciones simples tenemos que A Bt + D 3t6 − 6t3 = 3t3 − 3t + + 2 . 2 (t − 1)(t + t + 2) (t − 1) t + t + 2 Luego Z √ Z Z Z Z dt x32+x Bt + D 3 √ dx = 3 t dt − 3 tdt + A + dt 3 (t − 1) t2 + t + 2 x+ 2+x De esta forma, exceptuando la integral Calculemos así la integral faltante. Z Z Bt + D dt, todas las integrales son directas. +t+2 t2 Bt + D dt = 2 t +t+2 Z (t2 Bt + D dt + 12 )2 + 47 1 1 Llamemos u = t + . Así, t = u − y dt = du, y por lo tanto 2 2 Z Bt + D dt = 2 (t + 12 )2 + 47 Z = B 2 = B 2 = B 2 Z Z B(u − 12 ) + D u du dt = B 7 7 du + D 2 2 2 u +4 u +4 u + u D 7 2 + q arctan q ln u + 4 7 7 4 4 √ √ ! 2 7 7D 7u 2 + ln u2 + arctan 4 7 7 √ √ ! √ 2 2 7D 7t 7 ln(t2 + t + 2) + arctan + 7 7 7 7 4 95 2. Miscelánea de integrales De esta forma Z 3t6 − 6t3 3t4 3t2 = − + A ln |t − 1| + (t − 1)(t2 + t + 2) 4 2 √ √ 2 7t 2 7D arctan + + 7 7 B ln(t2 + t + 2) 2 √ ! 7 7 3t4 3t2 − + A ln |t − 1| + 4 2 √ √ 2 7D 2 7t + arctan + 7 7 B ln(t2 + t + 2) 2 √ ! 7 , 7 = y finalmente √ √ √ Z √ 3( 3 x + 2)4 3( 3 x + 2)2 x32+x 3 √ dx = − + A ln | x + 2 − 1| 3 4 2 x+ 2+x √ √ B + ln(( 3 x + 2)2 + 3 x + 2 + 2) 2 √ √ ! √ √ 2 7D 2 73 x+2 7 + arctan + 7 7 7 3 15 3 Ahora bien, calculando los coeficientes tenemos que A = − , B = yD=− . 4 4 2 Z xarcsenx p 58. dx (1 − x2 )3 Aplicamos integración por partes para calcular esta integral. dx 1− Z x2 xdx p dx −→ v = (1 − x2 )3 u = arcsenx −→ √ x dv = √ ( 1 − x2 )3 xdx p , para continuar con la integral que deseamos (1 − x3 )3 Z Z 3 1 xdx p +C dx = x(1 − x2 )− 2 dx = − √ v= 1 − x2 (1 − x2 )3 Así, calculemos la integral calcular. Z De esta forma Z Z Z 1 1 arcsenx 1 xarcsenx arcsenx p √ + √ dx = − √ + dx dx = − √ 2 2 2 2 2 3 1 − x2 1−x 1−x 1−x 1−x (1 − x ) 1+x 1 arcsenx +C + ln = −√ 2 2 1−x 1−x 96 59. 2.2. Solución de los Ejercicios Propuestos Z xex dx (x + 1)2 Notemos que Z xex dx = (x + 1)2 Z Z (x + 1 − 1)ex (x + 1)ex ex = dx − dx (x + 1)2 (x + 1)2 (x + 1)2 Z Z ex ex = dx − dx (x + 1) (x + 1)2 Z Ahora bien, apliquemos el método de integración por partes a tomemos 1 dx u= −→ du = − 1+x (1 + x)2 x x dv = e dx −→ v = e Así Z ex xex dx = − (x + 1)2 (x + 1) R ex dx. (x+1) Para ello Z (−1) ex e dx − dx (x + 1)2 (x + 1)2 Z Z ex ex ex = + dx − dx (x + 1) (x + 1)2 (x + 1)2 Z x ex +C (x + 1) = Resolvamos esta misma integral, pero ahora haciendo uso del método de integración por parte en forma directa u = xex −→ du = (ex + xex )dx 1 dx −→ v = − dv = (1 + x)2 1+x De esta manera tenemos que Z xex xex dx = − + (x + 1)2 1+x = − 60. Z Z xex ex + xex dx = − + 1+x 1+x Z xex ex (1 + x) dx = − + 1+x 1+x xex −xex + xex + ex ex + ex + C = +C = +C 1+x 1+x 1+x ln(2x) dx x ln(4x) Notemos que Z ln(2x) dx = x ln(4x) Z ln 2 + ln x 1 dx = ln 4 + ln x x Z ln 2 + ln x 1 dx 2 ln 2 + ln x x Z ex dx 97 2. Miscelánea de integrales 1 . De esta forma x Z Z Z Z ln 2 + t ln 2 + t 2 ln 2 + t − ln 2 ln(2x) dx = dt = dt = dt x ln(4x) 2 ln 2 + t 2 ln 2 + t 2 ln 2 + t Z Z Z ln 2 dt = 1− dt = dt − ln 2 2 ln 2 + t 2 ln 2 + t Consideremos el cambio de variable t = ln x de donde dt = = t − ln 2 ln | ln 2 + t| + C = ln x − ln 2 ln | ln 2 + ln x| + C = ln x − ln 2 ln | ln 2x| + C 61. Z x cos4 xdx Calculemos esta integral haciendo uso del método de integración por parte. Tomemos así u = x −→ du = dx 2 Z 1 + cos(2x) 4 dv = cos xdx −→ v = dx 2 2 Z 1 + cos(2x) dx, para así poder calcular la De esta forma, calculemos primero 2 integral que nos interesa. 2 Z Z 1 + cos(2x) 1 + 2 cos2 x + cos2 (2x) dx dx = 2 4 Z Z Z 1 1 1 + cos(4x) 1 dx + cos(2x)dx + dx = 4 2 4 2 Z Z Z Z 1 1 1 1 dx + cos(2x)dx + dx + cos(4x)dx = 4 2 8 8 Z Z Z 3 1 1 = dx + cos(2x)dx + cos(4x)dx 8 2 8 = 3x sen(2x) sen(4x) + + +C 8 4 32 3x sen(2x) sen(4x) + + , y finalmente 8 4 32 Z Z 3x sen(2x) sen(4x) 3x sen(2x) sen(4x) 4 − dx + + + + x cos xdx = x 8 4 32 8 4 32 2 3x2 xsen(2x) xsen(4x) 3x cos(2x) cos(4x) = +C + + − − − 8 4 32 16 8 128 De esta manera v = 98 2.2. Solución de los Ejercicios Propuestos BIBLIOGRAFÍA 99 100 2.2. Solución de los Ejercicios Propuestos BIBLIOGRAFÍA [1] S. L. Salas, y E.Hille, Calculus: una y varias variables, Vol.1, New York, Reverté S.A., 1984. [2] I. A. Maron, Problems in calculus of one variable, Russian, 1973. [3] B. Demidovich, Problemas y ejercicios de análisis matemático, Mir Moscú, 1977. [4] Earl Swokowski, Cálculo con geotería analítica, Iberoamérica, 1988. 101