Nathalie Sepúlveda Delgado Guía de Trabajo n° 1 Segundo medio Fu

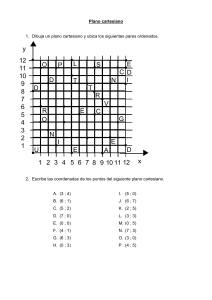
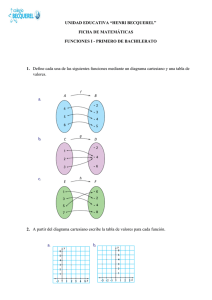
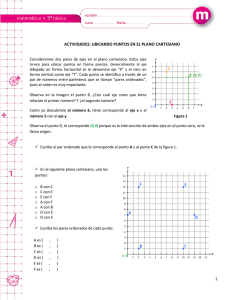
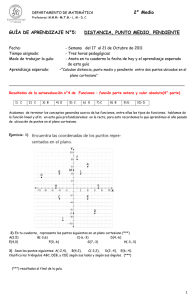
Colegio Antil Mawida
Departamento de Matemática
Profesor: Nathalie Sepúlveda Delgado
Guía de Trabajo n° 1 Segundo medio
Funciones
N°
1
Fecha
Tiempo 2 Horas
Nombre del/la alumno/a
Unidad Nº 3
Álgebra
Núcleos temáticos de Funciones
la Guía
Objetivos de la Guía
Recordar, comprender y aplicar conceptos asociados a producto
cartesiano, relaciones y funciones.
Aprendizaje
Recuerdan, comprenden y aplican conceptos asociados a
Esperado
producto cartesiano, relaciones y funciones.
PRODUCTO CARTESIANO
Dados los conjuntos A y B , su producto cartesiano ( A × B ) está formado por cada uno de
los pares ordenados donde el primer elemento pertenece a A y el segundo a B :
𝐴 𝑥 𝐵 = { (𝑎, 𝑏) / 𝑎 Є 𝐴 𝑦 𝑏 Є 𝐵 }
Ejemplo:
Si A = { a, b, c } y B = { 1, 2 } , entonces:
A x B = { (a,1), (a,2), (b,1), (b,2), (c,1), (c,2)}
RELACIONES:
Una “relación R” de un conjunto A a un conjunto B (R: A
B), es un subconjunto del
producto cartesiano entre A y B (A x B), determinado por una, o más condiciones.
Ejemplo:
Si A = {2, 3, 7} y B = {4, 5, 6} y R una relación de A en B tal que:
R = { (a,b) Є A x B / b es múltiplo de a} entonces:
A x B = {(2,4); (2,5); (2,6); (3,4); (3,5); (3,6); (7,4); (7,5); (7,6)}
R = {(2,4); (2,6); (3,6)} A x B
Utilizaremos el ejemplo anterior para explicar algunos conceptos.
R = {(2,4); (2,6); (3,6)} A x B
Dominio: Es el conjunto formado por todos los elementos del conjunto de partida que son
pre-imagen de algún elemento del conjunto de llegada.
Recorrido: Es el conjunto formado por todos los elementos del conjunto de llegada que son
imagen de algún elemento del conjunto de partida.
Conj. de partida
Pre-imágenes {2,3}
Dominio y Recorrido
Conj. de llegada (Codominio)
Imágenes {4,6}
Ejemplo:
Si A = {2, 3, 7} y B = {4, 5, 6} y R una relación de A en B tal que:
R = {(2,4); (2,6); (3,6)}  A x B , entonces:
Dom(R): = {2,3}
Rec(R): = {4,6}
FUNCIÓN
Una “función f” es una relación, tal que todo elemento del conjunto de partida tiene
imagen, y ésta es única.
• Dom f = A (ocupados)
•
Ningún elemento del dominio tiene más de una imagen. (fieles)
Ejemplos: 1. Determine si la siguiente relación R es función:
2. Determine si la siguiente relación R es función:
EVALUACIÓN DE FUNCIONES
Ejemplo 1: Sea f una función, definida en los reales como: f(x) = 2x + 3.
Para f(x) = 2x + 3, determinar :
a) f(4)
b) f(0)
c) f(-1)
Dominio y Recorrido
f(x) = 2x + 3 es “función afín”, Dom(f)=IR y Rec(f)=IR
Ejercicio:
Indicar si los siguientes gráficos corresponden a funciones, determinando el dominio y
recorrido de aquellos que representen una función.
Ejercicios