VARIABLES ALEATORIAS Y DISTRIBUCIÓN DE PROBABILIDADES
Anuncio

VARIABLES ALEATORIAS Y DISTRIBUCIÓN DE
PROBABILIDADES
HAMLET MATA MATA PROF. DE LA UNIVERSIDAD
POLITÉCNICA DE EL TIGRE-VENEZUELA
http://hamletyestadisticaspss.jimdo.com/
Variable Aleatoria es una función que asocia un número real, perfectamente
definido, a cada punto muestral. A veces las variables aleatorias (va) están ya
implícitas en los puntos muestrales.
EJEMPLO 1: Sea el evento, la experiencia relacionada con la medición de la
estatura de 100 individuos. Un punto muestral (resultado de un experimento) es
ya un número (estatura). La va está implícita.
EJEMPLO 2: Sea el evento, lanzar una moneda 3 veces al aire. Si se representa
la cara con c y el sello con s, entonces el espacio muestral será:
Espacio Muestral = {ccc, ccs, csc, scc, css, scs, ssc, sss}
La probabilidad de cada suceso elemental es 1/8. Por ejemplo p(ccc) = 1/8, ya
que la probabilidad de sacar cara en una tirada es 1/2 según la definición clásica y
las tiradas son independientes.
DEFINIMOS LA VARIABLE ALEATORIA X: número de caras, que puede tomar
los valores {0, 1, 2, 3}. Se buscan todos los puntos muestrales que dan lugar a
cada valor de la variable y a ese valor se le asigna la probabilidad del suceso
correspondiente.
x
Sucesos
px
0
{zzz}
1/8
1
{czz, zcz,
zzc}
3/8
2
{ccz, czc,
zcc}
3/8
3
{ccc}
1/8
En el caso de las variables discretas, como en el ejemplo, es una función que para
cada valor de la variable da su probabilidad.
EJEMPLO 3. Sea el evento experimental, lanzar al aire 2 monedas. Se sabe que el
espacio muestral de este experimento contiene 4 puntos muestra les.
S = {(c, c), (c, s), (s, c), (s, s)}, donde el primer elemento de cada par indica si
se obtuvo cara (c) o sello (s) en la primera moneda, y el segundo lo mismo con
respecto a la segunda moneda. La probabilidad de cada punto muestral es
entonces 1/4. Ahora bien, normalmente
no estamos interesados en los puntos
muestrales, sino en cierta magnitud asociada con los puntos muestrales. Por Ej.
Se podría estar interesado en el número de caras que hay en cada punto
muestral. Si definimos una variable Xi como el número de caras en el punto
muestral si, Xi tomará los valores X1 = 2, X2 = 1, X3 = 1, X4 = 0. Por lo tanto,
Xi es una variable aleatoria.
Una variable X es una variable aleatoria si es una magnitud susceptible de tomar
diversos valores con determinadas probabilidades. Es una regla que asocia un
número con cada evento simple en el espacio muestra de un experimento. Por lo
general, esta regla se simboliza por medio de las mayúsculas X, Y o Z.
DEFINICIÓN: Una variable aleatoria es una función que asocia un número
real a cada elemento del espacio muestral. O también, Una Variable
Aleatoria es una función que asigna un número real a cada resultado en
el espacio muestral de un experimento aleatorio.
Una variable es aleatoria si toma diferentes valores como resultado de un
experimento aleatorio. Esta variable aleatoria puede ser discreta o continua. Si
puede tomar sólo un número limitado de valores, entonces es una variable
aleatoria discreta. En el otro extremo, si puede tomar cualquier valor dentro de un
intervalo dado, entonces se trata de una variable aleatoria continua.
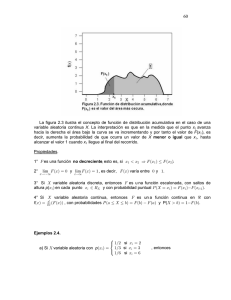
La distribución de probabilidad X se describe por una fórmula que enuncia la
probabilidad como una función de x. Es decir, la distribución de X está especificada
por la función f x ( x) P( X x) . El subíndice de f x (x) revela la variable aleatoria de
interés. El subíndice se omitirá cuando no
halla ninguna confusión sobre la
probabilidad del resultado. Puesto que f x (x) está definida como una probabilidad,
f x (x) es una función que va del conjunto de valores posibles de la variable
aleatoria al intervalo [0, 1].
DEFINICIÓN: La función f x (x k ) P(X x k ), k 1,2,3,...
que va del conjunto
de los valores posibles de la variable aleatoria discreta X al intervalo [0, 1]
recibe el nombre de función de probabilidad. Para una variable aleatoria
X , f x ( x)
satisface las siguientes propiedades:
1..... f x ( x k ) P(X x k )
2....f x ( x k ) 0,...
3....
Para todo x.
f x (x k ) 1
x
Se ha esgrimido el término experimento estadístico para representar cualquier
proceso a través del cual se generan diversas observaciones al azar. Con
frecuencia no interesan los detalles asociados con cada punto muestral, sino
simplemente alguna descripción numérica del resultado. Por ejemplo, el espacio
muestral que da una descripción detallada de cada uno de los resultados posibles
de los alumbramientos de una mujer en 3 ocasiones, pueden escribirse así:
S = (Espacio Muestral) = {HHH, HHM, HMH, MHH, HMM, MHM, MMH, MMM}
Si lo que interesa es sólo el número de hembras que alumbra la mujer, entonces
se podría asignar un valor numérico de 0, 1, 2 ó 3 a cada uno de los puntos
muestrales.
Los números 0, 1, 2 y 3 son cantidades aleatorias que se determinan a través del
resultado del experimento. Se podría pensar como los valores que toma alguna
variable aleatoria X, que en este caso representa el número hembras que nacen
cuando la mujer tiene 3 alumbramientos.
DEFINICIÓN: Si un espacio muestral contiene un número finito de posibilidades o
una secuencia sin final con igual número de elementos que números enteros, se
le denomina variable aleatoria discreta (espacio muestral discreto). A una
variable aleatoria se le denomina variable aleatoria discreta si su conjunto de
posibles resultados es contable. Las distribuciones discretas son aquellas en
las que la variable puede pude tomar un número determinado de valores.
Las variables aleatorias discretas representan datos que se refieren, tales
como el número de artículos defectuosos en una muestra de m de ellos o el
número de accidentes en carreteras por año en un estado determinado.
EJEMPLO: si se lanza una moneda al aire puede salir cara o cruz; si se tira un
dado puede salir un número de 1 al 6; en una ruleta el número puede tomar un
valor del 1 al 32.
El resultado de un experimento estadístico que puede no ser finito ni contable. Un
ejemplo de este paradigma ocurre cuando se produce
una investigación para
medir las distancias que recorre cierta marca de automóvil en una distancia de
prueba especificado con 5 litros de gasolina. Asumiendo que el trayecto es una
variable que se puede medir con cualquier grado de precisión, entonces resulta
claro que se tiene un número infinito de distancias posibles en el espacio muestral
y que no puede igualarse al número de números enteros. Si se registrara también
la cantidad de tiempo en que se efectúa el recorrido de la diferentes marcas, da
nueva cuenta de los intervalos de tiempos posibles que conforman el espacio
muestral serian infinitos en número e incontables. Se observa con esto que no
todos los espacios muestrales son necesariamente discretos.
DEFINICIÓN: Si un espacio muestral
contiene un número infinito de
posibilidades iguales al número de puntos que se encuentran en un segmento de
línea, se le denomina variable aleatoria continua (espacio muestral
continuo). Las distribuciones continuas son aquellas que presentan un número
infinito de posibles soluciones. Cuando una variable aleatoria puede tomar valores
en una escala continua, se le denomina variable aleatoria continua.
EJEMPLO: El peso medio de los alumnos de una clase puede tomar infinitos
valores dentro de cierto intervalo (42,37 kg, 42,3764 kg, 42, 376541kg, etc); la
esperanza media de vida de una población (72,5 años, 7,513 años, 72, 51234
años).
Con frecuencia, los valores posibles de una variable aleatoria continua son
precisamente los mismos valores contenidos en el espacio muestral continuo. Tal
es el caso de aquella variable aleatoria que representa la distancia que cierta
marca de automóvil puede recorrer, en un camino de prueba, con 5 litros de
gasolina. En la mayoría de los problemas prácticos, las variables aleatorias
continuas representan datos medidos, tales como alturas, pesos, temperaturas,
distancias o períodos de vida posibles.
Se puede especular en una variable aleatoria como un valor o una magnitud que
cambia de un desarrollo a otra, sin seguir una secuencia predecible. Por ejemplo,
en un hospital para tratamiento del cáncer de pulmón no se tiene manera de
saber con exactitud cuántos hombres van a ser atendidas en un día cualquiera. Si
los registros diarios del hospital indican que los valores de la variable aleatoria van
desde 100 hasta 115 pacientes diarios, entonces ésta es una variable aleatoria
discreta.
Una variable aleatoria es discreta cuando únicamente puede tomar un
determinado número de valores en un intervalo. Por ejemplo, la variable aleatoria
N° de caras obtenidas al lanzar 2 monedas, es una variable aleatoria discreta en
el intervalo (0,2). Solo puede tomar los valores 0, 1 y 2. Si el espacio muestral
consiste en un Conjunto discontinuo de sucesos, entonces una variable asociada
con ese conjunto se le llama discreta; de otra manera, se le llama continua.
Una variable aleatoria es continua cuando puede tomar cualquier valor en un
intervalo. Supongamos el experimento de lanzar una moneda hacia una línea
marcada en el suelo. Supongamos que la distancia máxima a que puede caer la
moneda de la marca es 1 metro (entendiendo como distancia la del centro de la
moneda a la línea). Si definimos una variable aleatoria X que represente esa
distancia, X puede tomar cualquier valor en el intervalo [0,1].
DISTRIBUCIONES DE PROBABILIDAD PARA VARIABLES
ALEATORIAS
Una variable aleatoria es un evento numérico cuyo valor se
determina
mediante un proceso al azar. Cuando se asignan valores de probabilidad a todos
los datos numéricos posibles de una variable aleatoria X, ya sea mediante un
listado o a través de una función matemática, se obtiene como resultado una
distribución de probabilidad. La suma de las probabilidades para todos los
resultados numéricos posibles debe ser Igual a 1.0. Pueden denotarse los valores
de probabilidad individuales mediante el símbolo f(x), lo cual implica que hay
implícita una función matemática; mediante P(x = X), lo cual implica que la
variable aleatoria puede asumir diversos valores específicos, o simplemente
mediante P(X).
Para una variable aleatoria discreta, se pueden enumerar todos los valores
numéricos posibles de la variable en una tabla con las probabilidades
correspondientes. Existen diversas distribuciones estándar de probabilidad que
pueden utilizarse como modelos para una amplia gama de variables aleatorias
discretas en aplicaciones de negocios.
Para una variable aleatoria continua no es posible enumerar todos los posibles
valores fraccionarios de la variable y, por lo tanto, las probabilidades que se
determinan a través de una función matemática se ilustran en forma gráfica
mediante una función de densidad de probabilidad o curva de probabilidad.
EJEMPLO 1. En la Tabla A se muestra el número de camionetas que se han
solicitado para rentar en una arrendadora de automóviles, en un periodo de 50
días. En la última columna de la Tabla se incluyen las frecuencias observadas en
este periodo de 50 días. En la última columna de la tabla se incluyen las
frecuencias observadas en ese periodo de 50 días, convertidas en probabilidad.
Así, puede observarse que la probabilidad de que se hayan solicitado exactamente
siete camionetas en un día elegido al azar en ese periodo es de 0.20, y que la
probabilidad de que se hayan solicitado seis o más es de 0.28 + 0.20 + 0.08 =
0.56.
Tabla B. Demanda diarios de arrendamiento de camionetas
Durante un periodo de 50 días.
Demandas
Número
de Probabilidad P(X )
Valor
Posibles X
Días
Ponderado X .P( X )
3
3
0.06
0.18
4
7
0.14
0.56
5
12
0.24
1.20
6
14
0.28
1.68
7
10
0.20
1.40
8
4
0.08
0.64
E ( X ) 5.66
TOTALES
50
1.00
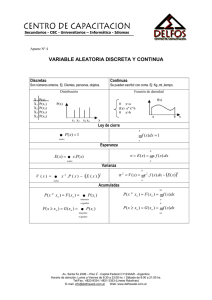
DISTRIBUCIONES DE PROBABILIDAD PARA VARIABLES
DISCRETAS
Las variables aleatorias, son aquellas que se relacionan con la ocurrencia de un
fenómeno aleatorio. Cuando una de esas variables aleatorias toma diversos
valores, la probabilidad asociada a cada uno de tales valores puede ser organizada
como una distribución de probabilidad, lo que se denomina distribución de las
probabilidades asociadas a cada uno de los valores de la variable aleatoria. Las
distribuciones de probabilidad logran representarse a través de una tabla, una
gráfica o una fórmula, en cuyo caso tal regla de correspondencia se le denomina
función de probabilidad.
VARIABLES ALEATORIAS DISCRETA: La variable aleatoria X se dice que es
discreta si los números asignados a los sucesos elementales de E son puntos
aislados. Sus posibles valores constituyen un conjunto finito o infinito numerable.
Por ejemplo, supongamos el experimento consistente en lanzar tres veces una
moneda no trucada; si consideramos la variable aleatoria X = ”número de caras
obtenidas en los tres lanzamientos”, los valores que puede tomar esta variable
aleatoria son finitos (0,1,2,3).
Entonces, una variable aleatoria discreta adquiere cada uno de sus valores con
cierta probabilidad. En el proceso del lanzamiento de una moneda 3 veces, la
variable X, que representa el número de sellos, toma el valor 2 con una
probabilidad de 3/8, puesto que 3 de los puntos muestrales igualmente probables
dan como resultado 2 sellos y 1 cara. Si se suponen arreglos iguales para los
eventos simples del siguiente ejemplo:
Un empleado de un depósito le regresa, en forma aleatoria, tres herramientas de
seguridad, previamente revisados, a tres obreros de un taller. Si Saúl (S), Jesús
(J) y Boris (B), en ese orden, reciben una de las tres herramientas, enumere los
puntos muestrales para los órdenes posibles de devolución de las herramientas y
calcule los valores b de la variable aleatoria B que representa el número de
agrupaciones correctas.
SOLUCIÓN.- Si S, J y B representan las herramientas de Saul, Jesús y Boris
respectivamente, luego los arreglos posibles en los que podrían devolverse las
herramientas y el número de agrupaciones correctas serán:
b
Espacio Muestral
3
SJB
1
1
0
0
1
SBJ JSB JBS BSJ BJS
La probabilidad de que ningún obrero reciba de nuevo la herramienta que tenía,
es decir, la probabilidad de que B tome el valor de cero, es 1/3. Los posibles
valores b de B y sus probabilidades están dados por
b
P(B = b)
0
1
3
1
1
2
3
1
6
Obsérvese que los valores de b agotan todos los casos posibles y por ello las
probabilidades suman 1.
Con frecuencia, resulta conveniente representar todas las probabilidades de una
variable aleatoria X a través de una fórmula. Esta fórmula seria necesariamente
función de los valores numéricos x, que se denotarán por f(x), g(x), r(x) y así
sucesivamente. Por lo tanto, se escribe f(x) = P(X= x); es decir f (3) P(X 3) . Al
conjunto de pares ordenados (x, f(x)) se le denomina función de probabilidad o
distribución de probabilidad de la variable aleatoria discreta X.
DEFINICIÓN: El conjunto de pares ordenados (x, f(x)) es una función de
probabilidad o una distribución de probabilidad de la variable aleatoria discreta X
si, para cada posible resultado x,
1. f ( x) 0.
2. f ( x) 1.
3. P( X x) f ( x).
EJEMPLO.- Un envió de ocho computadoras similares para un distribuidor
contiene tres defectuosas. Si un comerciante hace una compra aleatoria de dos de
esas computadoras, localice la distribución de probabilidad para el número de
computadoras imperfectas.
SOLUCIÓN.- Sea X una variable aleatoria cuyos valores de x son los números
posibles de computadoras defectuosas adquiridas por el comerciante. Luego, x
puede se cualquiera de los números 0, 1 y 2. Entonces:
3 5
3 5
10
0 2
1 1 15 ,..
f (0) P(X 0)
,..
f
(
1
)
P
(
X
1
)
28
28
8
8
2
2
3 5
3
2
0
.f (2) P(X 2) 8
28
2
Por lo tanto, la distribución de probabilidad de X es:
x
f(x)
0
10
28
1
15
28
2
3
28
EJEMPLO: Analice la variable aleatoria X, como la cantidad de caras observadas
cuando se lanzan dos monedas al aire. El espacio muestral es el conjunto {CC, CS,
SC, SS} y se puede observar que la variable X puede tomar como valores 0, 1 y 2.
Calculando las probabilidades tenemos:
P(de no observar caras)
=
P(SS)
=
P(X=0)
=
¼
P(de observar una cara)
=
P(SC o CS) =
P(X=1)
=
2
P(de observar dos caras)
=
P(CC)
P(X=2)
=
¼
=
/4
Si ahora se organizan estos resultados en el siguiente cuadro:
X
0
P(X=x)
¼
1
2
/4
2
¼
Se alcanzará explicar por qué se usa el nombre "distribución de probabilidad". Con
esta información se puede construir un histograma como el siguiente:
PROBLEMA
Se Lanzan dos dados al aire. ¿Cuál es
en los dados sea menor que 8?
probabilidad de que la suma de los puntos
SOLUCIÓN: Si asumimos que todos los resultados observados al lanzar los dos
dados son equiprobables (si todos los sucesos elementales que lo integran tienen
la misma probabilidad) entonces el espacio muestral del experimento, con treinta
y seis posibles resultados, se presentan a continuación:
Tabla 1. Espacio muestral
resultante al lanzar dos dados
1
2
3
4
5
6
1
1,1
1,2
1,3
1,4
1,5
1,6
2
2,1
2,2
2,3
2,4
2,5
2,6
3
3,1
3,2
3,3
3,4
3,5
3,6
4
4,1
4,2
4,3
4,4
4,5
4,6
5
5,1
5,2
5,3
5,4
5,5
5,6
6
6,1
6,2
6,3
6,4
6,5
6,6
Como nos interesa la suma de los puntos observados, si obtenemos el resultado
(3, 5) le asignamos el valor 8, correspondiente a la suma de 3 y 5. Podemos
calcular la probabilidad de que la suma sea igual a 8, contando todos los
resultados donde la suma es ocho. El evento de que la suma es ocho contiene 5
resultados: {(2,6), (3,5), (4,4), (5, 3), (6,2)}; por lo tanto la probabilidad
deseada es 5/36. Podemos repetir este proceso con cada uno de los resultados
para obtener las siguientes sumas probables al lanzar dos de acuerdo con la
tabla 2.
Tabla 2. Distribución de probabilidad del total de
las sumas observadas al lanzar dos dados
Sumas
2
3
4
5
6
7
8
9
10
11
12
Probabilidades
1
36
2
36
3
36
4
36
5
36
6
36
5
36
4
36
3
36
2
36
1
36
Hemos encontrado la distribución de probabilidad de los valores posibles de la
suma al tirar dos dados. Si R representa el resultado observado en el dado rojo y
V el resultado que se observará en el dado verde, podemos expresar el valor que
nos interesa así: X = R + V. Antes de lanzar los dados no sabemos qué valores
observaremos para R y V, por lo tanto tampoco lo sabemos para X.
El valor que asumirá X puede variar de lanzada en lanzada, sujeto a la distribución
especificada en la tabla de arriba. Así X es una variable, que asume un número
finito de valores sujeto a una distribución de probabilidad. Este es un ejemplo de
una variable aleatoria discreta. Otros ejemplos son las variables R y V. En general,
si S es un espacio muestral con una medida de probabilidad P, definimos una
variable aleatoria como una función que asigna un número real a cada uno de
los elementos de S.
Interpretamos, por ejemplo X = 8 como el evento de que se observó el resultado 8
al lanzar los dos dados, es decir el evento {(2,6), (3,5), (4,4), (5, 3), (6,2)}
ocurrió. También asignamos a X = 8 la probabilidad de ese evento. Así vemos que
P(X=8) = P({ (2,6), (3,5), (4,4), (5, 3), (6,2)}) = 5/36= 0.14. Es usual denotar
las variables aleatorias por letras mayúsculas y los valores que puede asumir por
letras minúsculas.
En este caso la variable X puede asumir un valor
entre un conjunto finito de
valores posibles. Cualquier variable que pueda asumir un número finito de valores
decimos es una variable aleatoria discreta. También son variables aleatorias
discretas aquellas que pueden asumir un número muy grande o infinito de valores
que potencialmente podrían ser contados, tal como el número de habitantes del
planeta, el número de granos de maíz producidos en el planeta en una fecha
determinada, el número de los árboles de un país.
En la Tabla 2
vemos que a cada valor posible de X, le asignamos un número
correspondiente a su probabilidad. Así podemos definir otra función:
f(x) = P(X = x), para cada número x en el campo de valores de la variable X. Esta
función se llama la función de probabilidad o distribución de probabilidad de
la variable X. Para el ejemplo de la suma de los puntos al tirar dos dados, los
valores de esta función están dados en la Tabla 2, la cual se puede reescribir
usando los conceptos estudiados.
Tabla 3. Distribución de probabilidad del total
de las sumas observadas al lanzar dos dados.
x
2
3
4
5
6
7
8
9
10
11
12
f(x)
1
36
2
36
3
36
4
36
5
36
6
36
5
36
4
36
3
36
2
36
1
36
Vemos que f(x) nunca adquiere un valor menor de cero. Esto se debe a que f(x)
representa una probabilidad, la cual nunca puede ser menor de cero. De igual
manera f(x) nunca puede ser menor de 1. Si sumamos todos los valores que
puede tener f(x) obtenemos 1, debido a que estamos sumando las probabilidades
de que la variable aleatoria asuma uno de los valores establecidos. Por su
definición, la función de probabilidad tiene las siguientes características:
1.
f ( x ) 0 para todo valor x en su dominio.
2.
f ( x ) 1
( donde la sumatoria se extiende sobre todos los valores x en
x
el dominio de f.
Los valores de la función de probabilidad se pueden representar en una gráfica
como la siguiente:
Diagrama de la distribucion de probabilidad
de la suma de dos dados
0,18
0,16
Probabilidades
0,14
0,12
0,1
0,08
0,06
0,04
0,02
0
1
2
3
4
5
6
7
8
9
10
11
12
Sumas de dos dados
La probabilidad de observar (En la grafica) un valor particular de la variable
aleatoria, digamos X = 3 está dado por la altura de la barra sobre el 3, es decir,
P(X = 3) = 2/36 = 0.056. De igual manera, en vez de asociar la altura de la barra
con la probabilidad, podemos ver que el área de la barra sobre el 3 es 2/36
1
= 2/36 = 0.056 ya que la altura de la barra es 2/36 y su ancho es 1. Usar el área
de las barras para representar la probabilidad es muy útil para extender la noción
de probabilidad a otras variables.
Podemos usar el histograma de probabilidad para calcular probabilidades tal como
P(X 4). Vemos que P(X 4) = P(X =2 ó X =3 ó X =4) = P(X = 2) + P(X = 3) +
P(X = 4) , ya que los eventos donde X = 2, X = 3 y X = 4 son disjuntos. Entonces
P(X 4) = 1/36 + 2/36 + 3/36 = 6/36, sumando las áreas de la barras que están
sobre el 4 y a su izquierda. Debemos ser muy cuidadosos con las desigualdades,
ya que P(X 4) = 6/36, mientras que P(X< 4) = 3/26.
Extendiendo esta idea de probabilidades acumulativas, podemos definir otra
función partiendo de la distribución de probabilidad. Si X es una variable aleatoria
discreta, definimos la función de distribución de X o función de distribución
acumulativa de X de la siguiente manera:
f ( x) p( X i x) f ( x),..Para.... <x<
x i
Las propiedades de las distribuciones de variables discretas son dos, y que
posteriormente, al hablar de las distribuciones de variables continuas, se repetirán
de manera muy similar:
a) Todos los valores de la distribución son mayores o iguales que cero, y además
son menores o iguales que uno.
0 ≤ P(X=x) ≤ 1.
b) La suma de todas las probabilidades de la distribución es la unidad. Esta
demostración es para mostrar que la distribución probabilística binomial cumple
con tales propiedades.
f (x) P(X=x) = 1.
De donde se puede afirmar que: la suma de todas las probabilidades de los
eventos posibles de una variable aleatoria es igual a la unidad. Hay que recalcar
que estas propiedades se enuncian suponiendo que conocemos el valor de la
probabilidad, pero en la realidad esto no ocurre, es decir, que no sabemos la
probabilidad y lo que se hace es trabajar con estimaciones. Se puede observar que
en ningún caso las combinaciones toma valores negativos, y como p y q son
positivos o cero, entonces todos los valores de la distribución probabilística son
positivos o cero. Precisamente esto conlleva a modelos teóricos que estiman los
resultados, y los principales, son los que a continuación se exhiben:
MODELOS DE DISTRIBUCIONES DE PROBABILIDAD DE
VARIABLES DISCRETAS
UNIFORME. Es la distribución donde todos los eventos elementales tienen la
misma probabilidad. Por
ejemplo: tirar un dado, donde la
función P(X=x)=
1
/6 para valores de x = {1, 2, 3, 4, 5, 6}
BINOMIAL. Es la que manipula la distribución de la probabilidad de obtener cierta
cantidad de éxitos al realizar una cantidad de experimentos con probabilidad de
éxito constante y con ensayos independientes.
GEOMÉTRICA. Es la distribución de la probabilidad de realizar cierto número de
experimentos antes de obtener un éxito.
HIPERGEOMÉTRICA. Es similar a la binomial, pero con un tamaño de muestra
grande en relación al tamaño de la población.
DE POISSON. Es la distribución de la probabilidad de que ocurra un evento raro
en un periodo de tiempo, un espacio o un lugar. Modelos de distribuciones de
probabilidad de variables discretas
UNIFORME. Es la distribución donde todos los eventos elementales tienen la
misma probabilidad. Por
ejemplo: tirar un dado, donde la
función P(X=x)=
1/6 para valores de x = {1, 2, 3, 4, 5, 6}
BINOMIAL. Es la que manipula la distribución de la probabilidad de obtener cierta
cantidad de éxitos al realizar una cantidad de experimentos con probabilidad de
éxito constante y con ensayos independientes.
Geométrica. Es la distribución de la probabilidad de realizar cierto número de
experimentos antes de obtener un éxito.
HIPERGEOMÉTRICA. Es similar a la binomial, pero con un tamaño de muestra
grande en relación al tamaño de la población.
De Poisson. Es la distribución de la probabilidad de que ocurra un evento raro en
un periodo de tiempo, un espacio o un lugar.
La que más nos interesará de estas será la distribución binomial que explicaremos
posteriormente.
MEDIA Y DESVIACIÓN ESTÁNDAR DE UNA
DISTRIBUCIÓN DE PROBABILIDAD PARA VARIABLES
DISCRETAS
En una distribución de frecuencias para datos agrupados se calculaba la media,
xf , donde, ( ) es la media de la población, la cual
utilizando la fórmula,
n
f
puede expresarse como X .
n
Considerando la definición de probabilidad de un evento, P(X) es el cociente de la
frecuencia entre el número total de eventos (probabilidad frecuencial de
ocurrencia), por lo que la media de una distribución de probabilidad de una
variable discreta es:
x.P( x )
POR EJEMPLO: Consideremos la variable X del ejemplo de caras observadas en
dos lanzamientos de monedas. Es decir, X tal que su distribución de probabilidad
sea:
X
P(X=x)
0
¼
1
/4
2
¼
2
Entonces, para calcular su media ( ) se realiza la siguiente operación:
2
xP ( x) 0.
x 0
1
1
1
1. 2. 1
4
2
4
Análogamente, la varianza se definió como
procedimiento semejante al anterior se tiene:
2
2
f (x )2
n
, y haciendo un
( x )2 n
f
Finalmente, la varianza de una distribución de probabilidad de una
variable discreta será:
Entonces, la desviación estándar de una distribución de probabilidad de
una variable discreta es:
( x )2 P( x )
POR EJEMPLO: Considerando la misma distribución de probabilidad
anterior, su desviación estándar se calcula:
( 0 1 )2
del ejemplo
1
1
1
1
1
1
1 1
1
2
( 1 1 )2 ( 2 1 )2 1. 0. 1.
.
4
2
4
4
2
4
4 4
2
2
ESPERANZA MATEMÁTICA O VALOR ESPERADO DE UNA
VARIABLE ALEATORIA DISCRETA
Valor esperado de una variable aleatoria discreta
Si X es una variable aleatoria, y el experimento aleatorio que determina el valor
de X se repite muchas veces, entonces se obtiene una secuencia de valores para
X. Puede emplearse un resumen de estos valores, tal como el promedio ( x ), para
identificar el valor central de la variable aleatoria. La función de probabilidad de X
puede interpretarse como la proporción de ensayos en los que X = x. En
consecuencia,
no es necesario realizar el experimento muchas veces con la
finalidad de determinar el valor medio de X. La media de X puede calcularse corno
el promedio ponderado de los valores posibles de X, asignando al resultado x un
factor de ponderación
f x ( x ) P( X x ) .
La media ( x ) de una distribución de probabilidad es el valor esperado de su
variable aleatoria.
El valor esperado o Esperanza Matemática de una variable aleatoria
discreta se puede considerar como su promedio ponderado sobre todos los
resultados posibles siendo las ponderaciones la probabilidad relacionada con cada
uno de los resultados.
Esta medida de resumen se puede obtener multiplicando cada resultado posible
Xi por su probabilidad correspondiente P( X i )
y después sumando los productos
resultantes. Por lo tanto el valor esperado de la variable aleatoria discreta
X, representada como E (X ) , se puede expresar con
la siguiente formula
matemática:
N
x E ( X ) X i P( X i ) , donde:
i 1
X = Variable aleatoria de Interés.
Xi = Resultado i de X.
P( X i ) Probabilidad de ocurrencia del evento i de X.
i= 1, 2, 3, ....,N.
También, se puede decir que:
La media, Esperanza Matemática o valor esperado de una variable aleatoria
x o
discreta X, expresada por
E (X ), es:
x E ( X ) xf x ( x)
x
N
o
x E ( X ) X i P( X i ) .
i 1
La media de X puede interpretarse como el centro de la masa del rango de los
valores de X. Esto es, si se coloca una masa igual a f x (x)
en cada punto x de la
recta real, entonces E(X) es el punto donde la recta queda en equilibrio. Por
consiguiente, el término función de probabilidad puede interpretarse mediante
esta analogía con la mecánica.
MEDIA DE UNA VARIABLE ALEATORIA
Si se tiran dos monedas al aire 16 veces y X representa el número de caras que
ocurren por lanzamiento, entonces los valores de X pueden ser 0, 1 y 2.
Supóngase que en el experimento se obtienen cero caras 4 veces, una cara 7
veces y dos caras 5 veces. El promedio de caras por lanzamiento de las dos
monedas es entonces
(0)(4) (1)(7) (2)(5)
1.06.
16
Este es un valor promedio y no necesariamente un resultado posible del
experimento. Por ejemplo, el ingreso mensual promedio de un vendedor no es
probable que sea igual a alguno de sus cheques de pago mensuales.
Reestructúrese ahora el cálculo para el número promedio de caras resultantes, de
modo que tenga la siguiente forma equivalente
0
4
7
5
1 2 1.06.
16
16
16
Los números 4/16, 7/16 y 5/16 son las fracciones del total de lanzamientos que
resulta en 0, 1 y 2 caras, respectivamente. Estas fracciones son también las
frecuencias relativas que corresponden a los diferentes valores de X en el
experimento. En efecto, se puede calcular entonces la media o el promedio de un
conjunto de datos, si se conocen los distintos valores que intervienen y sus
frecuencias relativas, sin conocimiento alguno del número total de observaciones
en el conjunto de datos. Por consiguiente, si 4/16 ó 1/4 de los lanzamientos
resultan 0 caras; 7/16, una cara; y 5/16, dos caras, el número medio de caras por
lanzamiento seria 1.06, sin importar que el número total de lanzamientos sea de
16, 1 000 o aun de 10 000.
Utilícese ahora este método de las frecuencias relativas para calcular a la larga el
número promedio de caras por lanzamiento de dos monedas que podría esperarse.
Este valor promedio se conoce como media de la variable aleatoria X o media
de la distribución de probabilidad de X, y se representa como x , o
simplemente como , cuando esté claro de que variable aleatoria se trata.
También es común entre los estadísticos designar a este valor como Esperanza o
Expectativa Matemática, o bien como valor esperado de la variable X, y
representarla como E(X).
Suponiendo que se tiran al aire dos monedas normales, se tiene que el espacio
muestra1 para el experimento es
S = {CC, CS, SC, SS}
Donde es C cara y S sello.
Puesto que los 4 puntos muestrales son igualmente probables, se deduce que
P(X = 0) = P(SS) = 1 .
4
P(X = l) = P(SC) + P(CS) = 1 .
4
1
.
P(X = 2) = P(HH) =
4
Donde un elemento, por ejemplo, SC, indica que de la primera tirada resultó Sello,
seguida de una cara en la segunda tirada. Ahora bien, estas probabilidades son
justamente las frecuencias relativas que a la larga corresponden a los eventos
dados. Por consiguiente,
1
4
1
2
1
4
E ( X ) 0 1 2 1.0.
Esto significa que una persona que tira al aire 2 monedas una y otra vez, logrará
en promedio 1 cara por tirada.
EL método descrito para calcular el número esperado de caras en cada tirada de 2
monedas, indica que la media o valor esperado de una variable aleatoria discreta
puede obtenerse multiplicando cada uno de los valores x1 , x2 ,..., xn , de la variable
aleatoria X por su probabilidad correspondiente f ( x1 ), f ( x2 ),....., f ( xn ), y sumando
luego los resultados. Sin embargo, esto se verifica sólo si la variable aleatoria es
discreta. En el caso de variables aleatorias continuas, la definición del valor
esperado es en esencia la misma, sólo que las sumatorias se reemplazan por integrales.
EJEMPLO. Determine el número esperado de químicos en un comité de tres
personas seleccionado al azar de un grupo de 4 químicos y 3 biólogos.
SOLUCIÓN. Se considera que X representa el número de químicos en el comité.
La distribución de probabilidad de X está dada por
4 3
x 3 x
f(x)
, para x = 0, 1, 2, 3.
7
3
Aplicando la formula se calculan los diferentes f ( xi ) así:
4 3
4 3
4 3
4 3
1
12
18
0 3 0
1 31
2 3 2
3 33 4
f (0)
;..
f
(
1
)
;..
f
(
2
)
,..
f
(
3
)
35
35
35
35
7
7
7
7
3
3
3
3
Los cálculos
obtenidos son:
f(0) = 1/35, f(l) = 12/35, f(2) = 18/35, y f(3) = 4/35. Entonces,
1
12
18
4 60 12
1.70.
1 2 3
35
35
35
35 35 7
E ( X ) 0
Por lo tanto, si se selecciona al azar una y otra vez un comité de 3 miembros a
partir de un grupo de 4 químicos y 3 biólogos, el mismo contendría en promedio
1.7 químicos.
EJEMPLO.
En un juego de azar de un casino, se le paga a una persona 5
dólares si al tirar a aire 3 monedas obtiene solo caras o sellos, mientras que esta
persona deberá pagar 3 dólares si obtiene sólo una o dos caras. ¿Cuál es la
ganancia esperada de jugador?
SOLUCIÓN. El espacio muestral formado por todos los posibles resultados que
pueden obtenerse cuando se lanzan 3 monedas de manera simultánea, o en forma
equivalente si la moneda se lanzan 3 veces sucesivamente (C = cara, S = sello),
es
S = {CCC, CCS, CSC, SCC, CSS, SCS, SSC, SSS}. Se puede argumentar que
cada una de estas posibilidades es igualmente posibles y
ocurre con una
probabilidad igual a 1/8. Un enfoque alternativo seria aplicar la regla multiplicativa
de probabilidad para sucesos independientes con cada uno de los elementos del
espacio muestral (S), así:
1 1 1 1
P(CCS ) P(C ) P(C ) P( S ) . Recuerde que la probabilidad de salir cara es
2 2 2 8
igual a la de salir sello, es decir, ½.
La variable aleatoria de interés es X, que es la cantidad que el jugador puede
ganar; y los valores posibles de X 5 $ si ocurre el evento E1 CCC , SSS y - 3
$ si ocurre el evento E2 CCS , CSC, SCC; CSS , SCS , SSC.Si se observa que E1 y E2 se
presentan con probabilidad de ¼ y ¾ , respectivamente, se concluye que
1
4
3
4
E ( X ) 5 3 1.
Por lo tanto en este juego el apostador, en promedio, perderá 1 $ al lanzar las 3
monedas.
Un juego de azar se considera justo si en el promedio el jugador termina sin
pérdida o ganancia. Por lo tanto, un juego justo se define como aquel donde hay
una ganancia esperada de cero, es decir, 0 .
Se puede pensar en una variable aleatoria como un valor o una magnitud que
cambia de una presentación a otra, sin seguir una secuencia predecible. Por
ejemplo, en una clínica para tratamiento del cáncer de mamas no se tiene manera
de saber con exactitud cuántas mujeres van a ser atendidas en un día cualquiera.
De modo que el número de pacientes del día siguiente es una variable aleatoria.
Los valores de una variable aleatoria son los valores numéricos correspondientes a
cada posible resultado del experimento aleatorio. Si los registros diarios de la
clínica indican que los valores de la variable aleatoria van desde 100 hasta 115
pacientes diarios, entonces ésta es una variable aleatoria discreta.
En la tabla B se ilustra el número de veces que se ha alcanzado cada nivel durante
los últimos l00 días. Observe que en la tabla aparece una distribución de
frecuencias. Hasta donde creamos que la experiencia de los pasados 100 días es
un comportamiento típico, podemos utilizar este registro para asignar una
probabilidad a cada número posible de pacientes y encontrar una distribución de
probabilidad. Hemos hecho esto en la tabla B mediante la normalización de la
distribución de frecuencias observadas (en este caso, dividimos cada valor que
aparece en la columna de las frecuencias (fi) de la tabla B , el número total de días
en que se tomaron los registros (número atendido). La distribución de probabilidad
para la variable aleatoria “número de atenciones diarias” se presenta de manera
gráfica en la figura I. Note que la distribución de probabilidad para una variable
aleatoria proporciona una probabilidad para cada valor posible y que estas
probabilidades deben sumar 1. De la misma forma en esa tabla se registra el valor
esperado o esperanza matemática que es simplemente la multiplicación de los
valores posibles de la variable aleatoria por la probabilidad de que la variable
aleatoria tome esos valores. En la tabla B mostramos que ambos requisitos se
cumplen. Además, tanto la tabla B como la figura I nos dan información acerca de
la frecuencia de presentación a la larga del número de pacientes atendidos
diariamente que esperaríamos observar si este “experimento” aleatorio se
efectuara de nuevo.
TABLA B
NÚMERO DE MUJERES ATENDIDAS DIARIAMENTE DURANTE 100
DÍAS EN UNA CLÍNICA PARA LA ATENCIÓN DE CÁNCER DE MAMA.
Valores
posibles de la
Variable
Aleatoria.
(1)
100
101
102
103
104
105
106
107
108
109
110
110
112
113
114
115
TOTALES
Número de
días que se
observa este
nivel (fi).
(2)
1
2
3
5
6
7
9
10
12
11
9
8
6
5
4
2
100
Probabilidad de que
la variable aleatoria
tome estos valores.
(3)
Esperanza
Matemática.
(1)x(3)
0.01
0.02
0.03
0.05
0.06
0.07
0.09
0.10
0.12
0.11
0.09
0.08
0.06
0.05
0.04
0.02
1.00
2.02
3.06
5.15
6.24
7.35
9.54
10.70
12.96
11.99
9.90
8.88
6.72
5.65
4.56
2.30
108.02
El valor esperado de la variable aleatoria “número diario de mujeres atendidas en
una clinica”, es igual 108.02.
0,14
Grafica correspondiente a la distribucion de
probabilidad para la variable aleatoria discreta,
"número diario de pacientes atendidos en una clinica"
0,12
PROBABILIDAD
0,1
0,08
0,06
0,04
0,02
10
10
0
10
1
10
2
10
3
10
4
10
5
10
6
10
7
10
8
10
9
11
0
11
1
11
2
11
3
11
4
11
5
0
Números diarios de mujeres atendidas
Si un agente de seguros afirma que puede esperarse que una mujer de 45 años
de edad viva otros 33 años, esto no significa que cualquier persona espere real-
mente que una mujer de 45 años siga viviendo hasta cumplir los 78 años y muera
al día siguiente. En lo concerniente a esa afirmación, ciertas mujeres de 45 años
vivirán 12 años más, otras sobrevivirán 25 años, otras vivirán 38 años más, . . . ,
y la expectativa de vida de “33 años más” se debe interpretar como una especie
de promedio particular, llamado valor esperado o esperanza matemática.
Originalmente, el concepto de la esperanza matemática apareció en relación con
juegos de azar y, en su forma más simple, se determina con el producto de la
cantidad que un jugador deposita para ganar y la probabilidad de que gane dicha
cantidad.
EJEMPLO ¿Cuál es nuestra esperanza matemática, si apostamos para ganar 500
bolívares, si y sólo si sale cara, al lanzar al aire una moneda equilibrada?
SOLUCIÓN: La moneda está equilibrada, de manera que la probabilidad de que
salga cara es ½, entonces
nuestra esperanza matemática es 500x0.5 = 250
bolívares.
EJEMPLO ¿Cuál es nuestra esperanza matemática, si compramos uno de los 1000
boletos de una rifa, en la que se ofrece como premio un televisor a color, que vale
480000 bolívares?
1
SOLUCIÓN: La probabilidad de que nos ganemos el televisor es
, entonces
1000
nuestra esperanza matemática es
1
480000
480000x
480 , es decir, 480 bolívares. Por lo tanto, en un sentido
1000
1000
estrictamente monetario, seria irracional pagar más
de 480 bolívares por el
boleto.
PROBLEMA. Sean 0.24, 0.35, 0.29 y 0.12 las probabilidades de que un usurero
pueda vender en un año un lote subdividido, con las respectivas ganancias de
Bs.1250000, Bs. 800000 o de Bs. 100000 o con una pérdida de Bs. 250000.
¿Cuál es la utilidad o ganancia esperada?
SOLUCIÓN: Si se sustituye
x1 1250000,...x 2 800000,..x3 100000,..x 4 250000,..
P1 0.24,..P2 0.35,..P3 0.25.. y..P4 0.12
.
Si ahora se aplica la fórmula matemática para la obtención de la Esperanza
Matemática se tiene:
N
x E ( X ) X i P( X i ) .
i 1
E 125000(0.24 80000(0.35) 10000(0.29) 25000(0.12) Bs.579000 . Este resultado indica
que el usurero espera ganar 579000 Bs. Con su usura.
PROBLEMA. La distribución de probabilidad de la variable aleatoria discreta X es
x
3 1 3
f ( x)
x 4 4
3 x
, x 0 ,1, 2, 3. Encuentre la esperanza matemática.
SOLUCIÓN:
0
3
3
0
2
2
27
27
3 1 3
3 1 3
3 1 3 9
f (0)
,... f (1)
,.. f (2)
64
64
0 4 4
1 4 4
2 4 4 64
1
3 1 3
f (3)
64
3 4 4
Con estos datos se puede formar la siguiente distribución de probabilidad:
x
f (x)
0
27
64
1
27
64
2
9
64
3
1
64
N
Aplicando la siguiente formula : x E ( X ) X i P( X i ) . Se tiene:
i 1
27
27
9
1 27 (2)9 (3)1 48 3
E 0 1 2 3
0.75.
64
64 4
64
64
64
64
Luego la esperanza matemática buscada es de 0.75.
FUNCIÓN DE DISTRIBUCIÓN ACUMULADA
En la teoría de probabilidades y estadísticas, la función de distribución
acumulativa (FDA), o simplemente función de distribución, describe la
probabilidad de que un valor real variable aleatoria X con una determinada
distribución de probabilidad se encontrará en un valor menor o igual que x. Las
funciones de distribución acumulativa también se utilizan para especificar la
distribución de múltiples variables aleatorias. Diremos que F es la Función de
distribución acumulada de probabilidad de X.
Si X es una variable aleatoria, entonces para cualquier número real x0, existe la
probabilidad P( X x0 ) del evento X x0 (X toma cualquier valor menor o igual a
x0). La probabilidad P( X x0 ) que depende de la elección de x0 es la probabilidad
acumulada hasta x0 que es la función distribución o distribución acumulada y
se denota por F(x0). Entonces, F ( x0 ) es igual a:
F ( x0 ) P X x0
p( x
X xi
0
)
OBSERVACIONES
1. F(xo) = P[X ≤ xo] = p(x1) + p(x2) + ... + p(xo)
2.
Si
X:
0,
1,
2,
3,
4
entonces
F(0) = P[X ≤ 0] = P(X < 0 ) + P(X = 0) = 0 + p(0) = p(0)
F(1) = P[X ≤ 1] = P(X ≤ 0) + P(X = 1) = p(0) + p(1)
F(2) = P[X ≤ 2] = P(X ≤ 1) + P(X = 2) = p(0) + p(1) + p(2)
F(3) = P[X ≤ 3] = P(X ≤ 2) + P(X = 3) = p(0) + p(1) + p(2) + p(3)
etc.
En general:
F(x)
=
P[X
≤
x-1]
+
P(X
=
x)
=
F(x-1)
+
p(x)
3. Si X: 0, 1, 2, 3, ..., n entonces: F(x) = 0 si X < 0. La acumulada siempre
empieza en 0. Siendo función de probabilidad, no puede tomar valores
negativos. F(x) = 1 si X ≥ n. Como en el caso anterior, siendo una función de
probabilidad no puede ser mayor que 1.
FORMA DE PRESENTAR LA DISTRIBUCIÓN ACUMULADA
Si la función de probabilidad de X viene dada por:
X
x1
x2
p( x )
p( x1 )
x3
x4
p( x2 ) p( x3 ) p( x4 )
La función de distribución acumulada F será:
CONSIDERACIONES
ACUMULADA
A
TOMARSE
F ( xi ) P X xi
EN
CUENTA
EN
LA
DISTRIBUCIÓN
p( x )
i
X xi
EJEMPLOS
Sea X una variable aleatoria discreta cuya función de probabilidad viene dada por:
X
0
1
2
3
p(x) 1/8 3/8 3/8 1/8
a) Obtenga
la
función
de
distribución
acumulada
de
b) Usando la distribución acumulada, encuentre P(X ≤ 2); P(X > 2);
b) P(1 ≤ X ≤ 2) y P(1 < X ≤ 2)
c)
d)
X
SOLUCIÓN
a) Recordemos que para todo valor de X menor que el mínimo valor implica que:
F(x) = 0
Del mismo modo, para X mayor o igual que el máximo valor de X, se tendrá
F(x) = 1
Tomando en cuenta estos criterios, la función acumulada viene dada por:
b)Puesto
P(X
que
F(a)
≤
=
2)
P(X
=
≤
F(2)
a),
entonces:
=
7/8
Usando complemento: P(X > 2) = 1 . P(X >2) = 1 - F(2) = 1 - 7/8 = 1/8
Usando propiedades: P(1 ≤ X ≤ 2) = F(2) - F(1) + P(X = 1) = 7/8 - 4/8 +
3/8
=
6/8
Del mismo modo, P(1 < X ≤ 2) = F(2) - F(1) = 7/8 - 4/8 = 3/8
Si X es una variable aleatoria, entonces para cualquier número real x0, existe la
probabilidad P( X x0 ) del evento X x0 (X toma cualquier valor menor o igual a
x0).
La probabilidad P( X x0 ) que depende de la elección de x0 es la probabilidad
acumulada hasta x0 que es la función distribución o distribución acumulada y
se denota por F(x0). F ( x0 ) P( X x0 )
Ejemplo 7: Encuentre los valores de la función distribución acumulada F(X) de la
variable aleatoria X descrita en el ejemplo 3.
X
f(X)
F(X)
2
1/36
1/36
3
2/36
3/36
4
3/36
6/36
5
4/36
10/36
6
5/36
15/36
7
6/36
21/36
8
5/36
26/36
9
4/36
30/36
10
3/36
33/36
11
2/36
35/36
12
1/36
36/36
Obsérvese que F(X=5) = f(X=2) + f(X=3) + f(X=4) + f(X=5) =
La gráfica de la función distribución acumulada de una variable discreta es siempre
una gráfica escalonada.
Fig. 6 Función distribución para la variable aleatoria del ejemplo 4.3
EJEMPLO 8: Halle los valores de la función distribución acumulada, F(X), de la
variable aleatoria X del ejemplo 5.
X f(X) F(X)
0 15/45 15/45
1 24/45 39/45
2 6/45 45/45
Ahora demostraremos que la probabilidad
de un evento
se
puede expresar en términos de la función distribución acumulada F(X), donde x1 y
x2 son dos de los valores cualesquiera
Obsérvese que
el evento
.
y
.
son eventos mutuamente exclusivos, su unión es
Por el axioma 3 de probabilidad, obtenemos
P(
) = P(
Despejando P
P
= P(
) + P(
)
se tiene
) - P(
) = F(x2) - F(x1)
En consecuencia, F(x) determina en forma única la distribución de probabilidades
de la variable aleatoria correspondiente.
FUNCIÓN DISTRIBUCIÓN
CONTINUAS:
PARA
VARIABLES
ALEATORIAS
Si X es una variable aleatoria continua, entonces la regla de la correspondencia
que define la función distribución acumulada F(X) es:
Hemos usado v para representar la variable de integración, ya que x se usa para
representar al límite superior de la integración. El integrando f es la función
densidad de probabilidad, y al derivar la expresión anterior (Teorema Fundamental
del Cálculo) se tiene que
La función distribución acumulada es
F(x0) =
PROPIEDADES DE LA FUNCIÓN DISTRIBUCIÓN ACUMULADA
2.
, si X es discreta
, si X es continua.
Fig. 4.7 Función distribución
3.
, si X es continua.
4. Si X es continua
EJEMPLO 4.9: Determinar el valor de la constante c tal que f(x) defina una
función densidad en el intervalo dado y determinar la regla de correspondencia de
la función de distribución acumulada correspondiente.
a.
,
b.
,
SOLUCIÓN: La integral sobre todo el intervalo es la probabilidad del espacio
muestral, que es igual a 1. Una vez evaluada la integral definida se despeja la
constante c, lo cual garantizará que la función obtenida es una función densidad
de probabilidad.
a.
b.
Sustituyendo el valor de c se obtiene la función densidad
La función distribución es entonces la integral de la función densidad para
cualquier intervalo (0,x), la cual permitirá calcular probabilidades para
cualquier intervalo.
c. Para el segundo caso se hará lo mismo que para el anterior con la diferencia
que tenemos una integral impropia.
La función densidad es entonces
Las propiedades de la función distribución acumulada son:
2.
, si X es discreta
, si X es continua.
3.
4.
, si X es continua.
Si
X
es
continua,
DISTRIBUCIONES DE VARIABLE DISCRETAS MÁS
IMPORTANTES
DISTRIBUCIÓN POISSON: La Distribución de Poisson es una distribución de
probabilidad discreta que enuncia, a partir de una frecuencia de ocurrencia media,
la probabilidad de ocurrencia de un determinado número de eventos durante cierto
periodo de tiempo. La función de masa de la distribución de Poisson es
Dónde: k es el número de ocurrencias del evento o
fenómeno (la función origina la probabilidad de que el evento suceda precisamente
k veces). λ es un parámetro positivo que significa el número de veces que se
espera que ocurra el fenómeno durante un intervalo dado. Por ejemplo, si el
suceso analizado ocurre en promedio 4 veces por minuto y estamos interesados en
la probabilidad de que ocurra k veces dentro de un intervalo de 10 minutos,
usaremos un modelo de distribución de Poisson con λ = 10×4 = 40. e es la base
de los logaritmos naturales (e = 2,71828 ...)
DISTRIBUCIÓN GEOMÉTRICA: La distribución geométrica es cualquiera de las
dos distribuciones de probabilidad discretas siguientes: la distribución de
probabilidad del número X del ensayo de Bernoulli necesaria para obtener un
éxito, contenido en el conjunto { 1, 2, 3,...} o la distribución de probabilidad del
número Y = X − 1 de fallos antes del primer éxito, contenido en el conjunto { 0, 1,
2, 3,... }. Cuál de éstas es la que uno llama "la distribución geométrica”, es
una cuestión de convención y conveniencia. Si la probabilidad de éxito en cada
ensayo es p, entonces la probabilidad de que x ensayos sean necesarios para
obtener un éxito es
,
para x = 1, 2, 3,....
Equivalentemente, la probabilidad de que haya x fallos antes del primer éxito es
para x = 0, 1, 2, 3,....
DISTRIBUCIÓN HIPERGEOMÉTRICA: La distribución hipergeométrica es
una distribución discreta relacionada con muestreos aleatorios y sin reemplazo.
Imagínese que se posee una población de N elementos de los cuales, d
pertenecen a la categoría A y N-d a la B. La distribución hipergeométrica mide la
probabilidad de obtener x (
) elementos de la categoría A en una
muestra de n elementos de la población original. La función de probabilidad de
una variable aleatoria con distribución hipergeométrica puede deducirse a través
de razonamientos combinatorios y es igual a
donde N es el tamaño de población, n es el tamaño
de la muestra extraída, d es el número de elementos en la población original
que pertenecen a la categoría deseada y x es el número de elementos en
N
la muestra que pertenecen a dicha categoría. La notación
hace
n
referencia al coeficiente binomial, es decir, el número de combinaciones
posibles al seleccionar n elementos de un total N.
DISTRIBUCIÓN UNIFORME DISCRETA: En teoría de la probabilidad, una
distribución uniforme discreta es una distribución de probabilidad que toma un
número finito de valores con la misma probabilidad, donde los elementos de un
conjunto finito son equiprobables. Si la distribución asume los valores reales
, su función de probabilidad es:
y su función de distribución la función escalonada
Su media estadística es
y su varianza
LA DISTRIBUCIÓN BINOMIAL
LA DISTRIBUCIÓN BINOMIAL es una distribución de probabilidad discreta que
mide el número de éxitos en una secuencia de n ensayos de Bernoulli
independientes entre sí, con una probabilidad fija p de ocurrencia del éxito entre
los ensayos. Estos experimento de Bernoulli se caracterizan por ser dicotómico,
vale decir, que únicamente son posibles dos resultados. A uno se le designa como
éxito y presenta una probabilidad de ocurrencia p y al otro se le llama fracaso,
con una probabilidad q = 1 - p. En la distribución binomial el anterior experimento
se repite n veces, de forma independiente, y se trata de calcular la probabilidad de
un determinado número de éxitos. Para n = 1, la binomial se convierte, de hecho,
en una distribución de Bernoulli. Para representar que una variable aleatoria X
sigue una distribución binomial de parámetros n y p, se escribe:
La función de probabilidad es
Donde
de en
(
y
elementos tomados de
Siendo las combinaciones
en
).
El nombre que recibe esta distribución se debe a la similitud existente entre la
distribución de las probabilidades
de obtener
0, 1, 2, 3,…..elementos
considerados como “éxito” de una muestra de tamaño
n, y los términos
n
sucesivos del desarrollo binomial ( p q ) , donde p expresa la probabilidad de
éxito de un solo ensayo (situación experimental), y q es la probabilidad de
“fracaso” (tal que, p + q = 1). En este caso, éxito significa encontrarse con
cierta clase de evento, mientras que fracaso significa no encontrarse con dicho
evento. En esta guía se hará un breve reposo del Teorema del binomio o
Binomio de Newton. El teorema del binomio, o Binomio de Newton por haber
sido éste quien propuso el método general para su desarrollo, es un binomio
elevado a una potencia n, que en su caso más simple es un número natural.
En términos generales, el teorema del binomio establece
que:
n
n
n
n
( a b ) a n a n1b .... abn1 b n
0
1
n1
n
n
n ni i
a b .
i 1 i
n
Para el caso concreto de esta guía, se cambiará la notación y se utilizará la
propiedad de conmutatividad de los números reales:
La probabilidad
Px de que un evento ocurra EXACTAMENTE
intentos esta dada por la ecuación:
x veces en
n
n x n x
Px . p q
.
x
La probabilidad Px de que un evento se presente POR LO MENOS
en n intentos esta expresada por la ecuación:
xn
x x
Px
x x
x x
x veces
n x n x
.
. p q
x
TRIÁNGULO DE PASCAL
Los coeficientes de los términos del desarrollo de cualquier potencia de un binomio
se pueden encontrar en forma inmediata utilizando el llamado triángulo de
Pascal. Los coeficientes del desarrollo de cualquier potencia de un binomio son los
números que se hallan en la fila horizontal en donde después del 1 esta el
exponente del binomio. Ejemplo: Los coeficientes del desarrollo del binomio
( a b )5 son aquellos números que se encuentran en la fila horizontal, del triángulo
de Pascal, en donde después del 1 esta el 5, es decir, 1, 5, 10, 10, 5, 1. De igual
manera se procede para ubicar los coeficientes de cualquier binomio.
El triángulo se forma de la siguiente manera: En la primera fila horizontal se
coloca 1. En la segunda fila se coloca 1 y 1. Desde la tercera fila en adelante se
comienza por 1 y cada número posterior al 1 se obtiene sumando en la fila
anterior el primer número con el segundo, el segundo con el tercero, el tercero
con el cuarto, cuarto con el quinto, el quinto con el sexto y así sucesivamente
hasta obtener los coeficientes de la potencia buscada, recuerde que el último
número de la fila horizontal siempre tiene que ser 1 (ver triángulo).
1
1
1
1
1
1
1
1
1
2
3
4
5
6
7
1
3
6
10
15
21
1
4
10
20
35
1
5
15
35
1
6
21
1
7
1
1
1
8
9
28
36
84
56
70
56
126
126
84
28
8
36
1
9
1
Ejemplo: Sean los binomios ( 2 x 3 y )5 y ( x y )5 , desarrolle los mismos aplicando
el triángulo de Pascal:
( 2 x 3 y )5 ( 2 x )5 5( 2 x )4 3 y 10( 2 x )3 ( 3 y )2 10( 2 x )2 ( 3 y )3 5( 2 x )( 3 y )4 ( 3 y )5
( 2 x 3 y )5 32 x 5 240 x 4 y 720 x 3 y 2 1080 x 2 y 3 810 xy 4 243 y 5 .
( x y )6 x 6 6 x 5 y 15 x 4 y 2 20 x 3 y 3 15 x 2 y 4 5xy 5 y 6 .
PROPIEDADES DE LA DISTRIBUCIÓN BINOMIAL
1.- El experimento se fundamenta en n ensayos repetidos.
2.- Cada ensayo proporciona un resultado que puede clasificarse como éxito o
fracaso. Cuando es éxito la variable toma el valor 1 y cuando es fracaso toma
el valor 0.
3.- La probabilidad de éxito, designada por p, permanece constante de un ensayo
a otro.
4.- Los ensayos son independientes.
EJEMPLOS 1: La Probabilidad de salir cara al lanzar una moneda al aire (sale cara
o no sale); la probabilidad de ser admitido en una universidad (o te admiten o no
te admiten); la probabilidad de acertar un Kino (o aciertas o no aciertas).
Al haber únicamente dos soluciones se trata de sucesos complementarios:
A la probabilidad de éxito se le denomina "p"
A la probabilidad de fracaso se le denomina "q"
Verificándose que:
p + q = 1.
EJEMPLOS 2: Probabilidad de salir cara al lanzar una moneda al aire:
Probabilidad de que salga cara: p = 0,5.
Probabilidad de que no salga cara: q = 0,5.
p + q = 0,5 + 0,5 = 1.
EJEMPLO 3: Probabilidad de ser admitido en la universidad:
Probabilidad de ser admitido: p = 0,25.
Probabilidad de no ser admitido: q = 0,75.
p + q = 0,25 + 0,75 = 1.
Ejemplo 4: Probabilidad de acertar un número de lotería de 100000:
Probabilidad de acertar: p = 0,00001.
Probabilidad de no acertar: q = 0,99999.
p + q = 0,00001 + 0,99999 = 1.
Considérense los siguientes experimentos y variables aleatorias
1.
Lanzar una moneda diez veces. Sea X = número de caras obtenidas.
2. IJna máquina herramienta desgastada produce 1 % ¡de partes defectuosas.
Sea X = número de partes defectuosas en las siguientes 25 que se produzcan.
3.
La posibilidad de que cada muestra de aire contenga una molécula rara es
10%. Sea X = número de muestras de aire que contienen la molécula rara en las
siguientes 18 muestras por analizar.
4. De todos los bits transmitidos por un canal de transmisión digital, el 10 % se
reciben con error. Sea X = número de bits con error en los siguientes cinco por
transmitir.
5. Un examen de opción múltiple contiene diez preguntas, cada una con cuatro
opciones, y se pide a una persona que adivine las respuestas. Sea X = número de
respuestas contestadas de manera correcta.
6.
De los siguientes 20 nacimientos en un hospital, sea X = número de
niñas.
7. De todos los pacientes que padecen una enfermedad en particular, el 35 %
experimenta una mejora con cierto medicamento. Para los siguientes
30
pacientes a los que se les administrará el medicamento, sea X = número de
pacientes que experimentan mejoría.
Estos ejemplos dejan entrever la utilidad de un modelo de probabilidad general
que incluya estos experimentos como casos particulares.
Cada uno de estos experimentos aleatorios pueden considerarse corno formado
por una serie de ensayos repetidos; 10 lanzamientos de la moneda en el
experimento (1), la producción de 25 partes en el experimento (2) y así
sucesivamente. En cada caso, la variable aleatoria es el conteo del número de
ensayos que cumplen con un criterio específico. Con esto, el resultado de cada
ensayo coincide o no con el criterio y X cuenta o no; en consecuencia, cada
ensayo puede resumirse como un éxito o un fracaso, respectivamente. Por
ejemplo,
en el experimento de opción múltiple, para cada una de las preguntas,
sólo la opción que es correcta es la que se considera como un éxito. La selección
de cualquiera de las otras tres opciones incorrectas da como resultado un ensayo
que puede resumirse como un fracaso.
Los términos éxito y fracaso son solo etiquetas. También pueden utilizarse para
este fin “A” “B” o “0” y "1". Por desgracia, en ocasiones las etiquetas usuales
pueden ser engañosas. En el experimento (2), dado que X es el número de
partes defectuosas, la producción de éstas es un éxito.
A menudo es razonable suponer que los ensayos que forman el experimento
aleatorio son independientes. Esto implica que el resultado de uno de los ensayos
no tiene ningún efecto sobre el resultado que se obtenga en cualquier otro ensayo.
En el experimento (2), la hipótesis de ensayos independientes implica saber que
la parte número 5 es defectuosa, no tiene ningún efecto sobre la probabilidad de
que cualquiera de las demás partes sea defectuosa. Asimismo, a menudo es
razonable suponer que la probabilidad de éxito en cada ensayo es constante. En el
experimento de opción múltiple [experimento (5)], si se supone que el sujeto que
lleva a cabo la prueba no tiene ningún conocimiento del tema y sólo adivina la
respuesta de cada pregunta, entonces puede considerarse que la probabilidad de
una respuesta correcta para cada pregunta es 1/4.
PROBLEMA VA : Sea el experimento binomial aquel donde se selecciona al azar
3 artículos de un proceso manufacturado, si se examinan y se clasifican como
defectuosos (D) o sin defectos, es decir, normales(N). Un artículo defectuoso se
considerara como un éxito. El número de éxitos es una variable aleatoria x que
toma valores enteros desde cero hasta 3. Los 8 posibles resultados y los
correspondientes valores de x son:
Resultados NNN
x
0
NDN
1
NND
1
DNN
1
NDD
2
DND
2
DDN
2
DDD
3
Los artículos se seleccionan en forma independiente de un proceso que produce
supuestamente 25 % de artículos defectuosos, entonces la probabilidad de
selección es
4143 4 9 64 .
P( NDN ) P( N )P( D )P( N ) 3
El número X de éxitos en n ensayo de un experimento binomial se llama
variable aleatoria binomial. La distribución de probabilidad de esta variable
aleatoria se le denomina distribución binomial y sus valores serán designados
por b(x, n, p), ya que dependen del número de ensayos y de la probabilidad de
éxitos en un ensayo
determinado. Por lo tanto, para la distribución de
probabilidad de X, el número de defectos en el problema antes planteado es
P( X x ) f ( x ) b( x.;..n;.. p ),
Generalizando la igualad anterior con el objeto de obtener una formula
matemática para b(x, n, p), que proporcione la probabilidad de x éxitos en n
ensayos en el caso de un experimento binomial. Primeramente se considerará la
probabilidad de x éxitos y de n – x fracasos en un orden especificado. Tomando
en cuenta que los ensayos son independientes, se pueden multiplicar todas las
probabilidades correspondientes a los diferentes resultados. Cada éxito ocurre con
una probabilidad
p y cada fracaso, con una probabilidad q = 1 – p. En
consecuencia, la probabilidad para un determinado pedido (del problema anterior)
es p x q n x . Se debe determinar ahora el número total de puntos maestrales en el
experimento que tiene x éxitos y n – x fracasos. Este número es igual al número
de particiones de n resultados en dos grupos, con x en un grupo y n – x en el
n
otro, el cual esta determinado por C( n ,x ) C x =
x
n
n!
(n! se lee factorial
x! ( n x )!
de n, donde por definición factorial de cero es igual 1). Como esas particiones son
mutuamente excluyentes, se suman las probabilidades de todas las particiones
x n x
diferentes para obtener la formula general o se multiplica p q
por
n
.
x
DEFINICIÓN DE DISTRIBUCIÓN BINOMIAL
Si un ensayo binomial puede resultar en un éxito con probabilidad p y en un
fracaso con probabilidad q = 1 – p, entonces en la distribución de probabilidad de
la variable aleatoria binomial X, el número de éxitos en
n
ensayos
independientes, es
n
b( x ,n , p ) f ( x ) . p x q n x ,.... x 0,1,2,3......, n
x
Esta es la fórmula de la distribución de probabilidad
binomiales.
para eventos
Observe el problema VA que cuando n = 3
y p =1/4, la distribución de
probabilidad de X, el número de defectos, se puede expresar así:
x
1
3 1 3
b x ,3, f ( x )
4
x 4 4
3 x
, x 0,1,2,3.
Aplicando Esta fórmula al problema VA se puede calcular la probabilidad de cada
evento así:
0
3
1
2
1
3
27
3 1 3
3 1
f ( 0 )
..., f ( 1 )
64
0 4 4
1 4
2
27
3
64
4
0
9
1
3 1 3
3 1 3
f ( 2 ) ..., f ( 3 )
64
2 4 4 64
3 4 4
La distribución de probabilidad del problema Va es:
x
f(x)
0
f ( x ) 27
1
64
27
2
64
9
3
64
1
64
EJEMPLO: La posibilidad de recibir de manera errónea un bit transmitido por un
canal de transmisión digital, es 0,1. Además, supóngase que los ensayos de
transmisión son independientes. Sea X = número de bits recibidos con error en
los próximos cuatro que serán transmitidos.
Calcule el espacio muestral de este experimento e indíquese el valor de X en cada
resultado. Calcúlese también, P(X = 2).
En este experimento se indica con E un bit erróneo, y con C un bit sin error, esto
es, recibido correctamente. Con esto, el espacio muestral de este experimento
puede describirse como una lista de cuatro letras que indican qué bits fueron
recibidos con y sin error. Por ejemplo, el resultado CECE indica que el segundo y el
cuarto bit son erróneos, y los otros dos se recibieron correctamente. Por
consiguiente, el espacio muestral es:
Resultado x
CCCC
0
CCCE
1
CCEC
1
CCEE
2
CECC
1
CECE
2
CEEC
2
CEEE
3
Resultado x
ECCC
1
ECCE
2
ECEC
2
ECEE
3
EECC
2
EECE
3
EEEC
3
EEEE
4
El evento en que X = 2 está formado por seis resultados:
S = {EECC, ECEC, ECCE, CEEC, CECE, CCEE}
Si se hace uso de la hipótesis de que los ensayos son independientes, entonces la
probabilidad de {EECC} es
P(EECC) = P(E)P(E)P(C)P(C) = (0.1)2(0.9)2 = 0.0081
Por otra parte, la probabilidad de que se presente cualquiera de los seis resultados
mutuamente excluyentes para los que X = 2, es la misma. Por consiguiente:
P(X = 2) = 6(0.0081) = 0.0486
En general,
P(X = x) =f(x)= (número de resultados con x errores) multiplicados por
(0.9)4-x
C\IlOs
(0.1)x
Para ultimar una fórmula general de probabilidad, únicamente es preciso una
expresión
para el número de resultados que contienen x errores. Puede
construirse un resultado que contiene x errores separando los cuatro ensayos en
dos grupos. El tamaño de uno de los grupos es x y contiene los errores, mientras
que el tamaño del otro grupo es n-x y está formado por los ensayos donde no hay
errores. Tomando en cuenta la ecuación de Combinación, el número de maneras
de separar cuatro objetos en dos grupos, uno de los cuales tiene tamaño x, es:
4!
4
. Por tanto, en este ejemplo,
x x! ( n x )!
4
4
x
4 x
P( X x ) f ( x ) ( 0.1 ) ( 0.9 ) P( X 2 ) f ( 2 ) ( 0.1 )2 ( 0.9 )42
x
2
P( X 2 ) f ( 2 ) 6( 0.01 )( 0.81 ) 0.0486 .
P( X 2 ) f ( 2 ) 0.0486 .
OTROS EJEMPLO
Los siguientes son ensayos Binomiales:
Un tornillo, puede estar defectuoso o no defectuoso.
El sexo de un bebé al nacer puede ser: niño o niña.
Las respuestas en una prueba determinada puden ser: correcta o incorrecta.
Si consideramos que una serie de ensayos Binomiales tiene como características:
1.
La probabilidad de éxito permanece constante, ensayo tras ensayo; y
2. Los ensayos son independientes entre sí;
3.
Entonces se tiene lo que se denomina experimento binomial, donde el número
de ensayos se denota con n, la probabilidad de éxito con p y la de fracaso con q.
Hay que notar que las probabilidades de éxito y de fracaso están relacionadas de
la siguiente manera: p + q =1.
POR EJEMPLO: Consideremos un examen con tres preguntas de opción múltiple,
con cuatro opciones, y que será contestado al azar.
Podemos utilizar el siguiente ejemplo:
1.Las
flores
de
la
cayena
a) rojas
b) azules
c) amarillas
d) naranjas
son
de
color:
2.Don
Cristóbal
Colon
a) 1592 b) 1692
c) 1492
d) 1792
3.El
significado
a) hoja
b) árbol
c) flor
de
d) fruto
descubrió
la
a
palabra
Venezuela
en:
planta
es:
Con los datos de esta prueba contamos con un experimento binomial, ya que la
probabilidad de éxito permanece constante en las tres preguntas (p = ¼) y las
respuestas de una a otra pregunta son independientes entre sí. Se cuenta con una
cantidad n = 3 de ensayos y q =1 – p = 3/4.
Hay que decir que n y p son los llamados parámetros de la distribución.
Tenemos ahora la variable aleatoria X del ejemplo anterior que representará el
número de respuestas correctas, siendo sus posibles valores: 0, 1, 2, y 3.
Para calcular la distribución de probabilidad correspondiente, consideraremos
como E los éxitos y como F los fracasos (el subíndice indica el número de
pregunta). Así pues, se tiene que:
P(X=
0)
= P(F1 F2 F3)
= P(F1)·P(F2)·P
(F3)
= (3/4 = 1·(3/4)3·(1
)3 =
/4)0
27
/6
4
P(X=
1)
= P[(E1 F2 F3) (F1 E2
F3)
(F1 F2 E3)]
=
P(X=
2)
= P[(E1 E2 F3) (E1 F2
E3) (F1 E2 E3)]
=
P(X=
3)
= P(E1 E2 E3)
P(X=x)
0
0.422
1
0.422
2
0.141
3
0.016
/2
= 3·(3/4)2·(1
/4)1
/64
= 3·(3/4)1·(1
/4)2
56
9
= P(E1)·P(E2)·P
(E3)
Al presentar esta información como tabla,
siguiente:
X
81
= (1/4 = 1·(3/4)0·(1
)3 =
/4)3
1
/64
su respectivo histograma seria el
EJEMPLO: Un estudio sobre la influencia relativa de esposos y esposas en las
políticas familiares de consumo, establece que el marido ejerce una influencia
decisiva en la compra de un automóvil nuevo, en lo referente a la marca, en 70 %
de las familias. Suponga que 4 familias han decidido comprar un automóvil nuevo.
a.- ¿Cuál es la probabilidad de que en exactamente 2 de las 4 familias los maridos
ejerza una influencia decisiva en la selección de la marca del automóvil a comprar?
b.- ¿Cuál es la probabilidad de que los maridos ejerzan una influencia decisiva en
la selección de la marca del automóvil en por lo menos 2 de las 4 familias?
c.- ¿Cuál es la probabilidad de que los maridos seleccionen la marca del automóvil
en las 4 familias?
SOLUCIÓN: Se supone que las decisiones de compras de las familias son
independiente y que p permanece constante de una familia a otra, por lo tanto, n
= 4, y p = 0.7. Sea x el número de familias en las cuales los maridos ejercen una
influencia decisiva en la selección de un automóvil nuevo. Por consiguiente, x = 0,
1, 2, 3 y 4, entonces se tiene que:
4
b( x ,4,0.7 ) f ( x ) 0.70 x 0.30 n x ,... x 0..,1..,2..,3..,4
x
4
a ). P( exactamente..dos ) P( x 2 ) f ( 2 ) .( 0.70 )2 ( 0.30 )2
2
4!
( 0.49 )( 0.09 ) 0.2646
2!.2!
Luego la probabilidad de que en exactamente 2 de las a familias los maridos
ejerzan una influencia decisiva en la selección de la marca de auto a comprar es
de 26.46 %.
b).- P(al menos dos) = tiene 2 soluciones posibles a saber:
1 ). P( x 2 ) p( 2 ) p( 3 ) p( 4 ),...o..tambien
2 ). P( x 2 ) 1 p( 0 ) p( 1 )
1 C 04 ( 0.7 )0 ( 0.3 )4 C14 ( 0.7 )1 ( 0.3 )3
1 0.0081 0.0756 1 0.0837
1 0.0837 0.9163
Entonces la probabilidad de que al menos en 2 de las familias el marido
seleccione la marca del automóvil nuevo es de 0.9163 = 91.63 %. La solución 1 se
le deja al estudiante para que la realice.
c).- P(4 familias) = C44 ( 0.7 )4 ( 0.3 )0
4!
( 0.7 )4 ( 1 ) 0.2401 .
4!.0!
La probabilidad de que los maridos de las 4 familias seleccionen la marca del
automóvil es de 0.2401 = 24.01 %.
PROBLEMA: Con el propósito de decidir si se aceptan los lotes de mercancía que
envía la fabrica RANICA a un comerciante, se lleva a cabo un procedimiento que
consiste en seleccionar 10 artículos al azar de cada lote y determinar el número
que presenta defectos. Un lote se rechaza siempre que se encuentren 2 o más
artículos defectuosos entre los 10 seleccionados. Se supone que el número de
artículos en cada lote es grande y que cada lote contiene un 5 % de artículos
defectuosos. ¿Cuál es la probabilidad de aceptar un lote de artículos? ¿Cuál es la
probabilidad de rechazarlo?
SOLUCIÓN: Sea x el número de artículos defectuosos observados; n 10 , y la
probabilidad de observar un articulo defectuoso en un ensayo es p = 0.05,
entonces:
10
p( x ) f ( x ) .( 0.05 ) x ( 0.95 )10 x , entonces las probabilidades de aceptar un lote
x
es:
1..P( aceptar ) p( 0 ) p( 1 )
2..P( aceptar ) 1
10
.( 0.05 ) x ( 0.95 )10 x
x2 x
10
1 ).P( aceptar ) p( 0 ) p( 1 ) C( 10,0 ) ( 0.05 )0 ( 0.95 )10 C( 10,1 ) ( 0.05 )1( 0.95 )9
P( aceptar ) ( 1 )(1 )( 0.599 ) ( 10 )( 0.05 )( 0.6302 ) 0.599 0.315
P( aceptar ) 0.914 91 .40 %.
a ).P( rechazar ) 1 P( aceptar 1 0.914 0.086 8.60 %...tambien.. puede..ser :
b ).P( rechazar )
10
.( 0.05 ) x ( 0.95 )10 x
x2 x
10
El estudiante debe realizar la parte 2 de la P( acetar ) y el resultado tiene que ser
igual al obtenido en la parte 1, (0.914). De la misma forma debe realizar los
cálculos de la parte b y el resultado tiene que ser igual al de la parte a (0.086).
LA MEDIA Y LA VARIANZA DE UNA VARIABLE ALEATORIA
BINOMIAL
El cálculo de p(x) puede ser muy aburrido cuando los valores de n son muy
grandes. Por tal razón, es conveniente describir la distribución de probabilidad
binomial mediante se media y su desviación estándar. Esto permitirá identificar
valores de x que son altamente improbables, usando el conocimiento sobre el
teorema de Tchebysheff y la regla empírica. Por lo tanto, es de gran importancia
conocer el valor esperado o esperanza matemática y la varianza de la variable
aleatoria binomial x.
La Media, la Varianza y la Desviación Estándar de una variable aleatoria Binomial
son:
E( x ) np
2 npq
npq
VARIABLE ALEATORIA CONTINUA
Una variable numérica puede clasificarse como discreta o continua. Las variables
discretas se miden utilizando números enteros y es posible asociarlas con la idea
de "contar". Las variables continuas se pueden asociar con la idea de "medir"
utilizando fracciones y decimales. Cuando la variable es continua el modelo
probabilístico que más se usa es la distribución normal. Las variables aleatorias
que hemos estudiado hasta ahora tienen la propiedad de que son el resultado de
contar; sus valores posibles varían en forma discreta (a saltos). Hay otro tipo de
variables aleatorias, las que son el resultado de un proceso de medir; sus valores
posibles cubren todo un intervalo en los números reales reales.
Cuando el espacio muestral de una variable aleatoria es un intervalo real decimos
que la variable es continua. La matemática que utilizamos para las variables
continuas es diferente a la de las discretas aunque los conceptos probabilísticos
sean los mismos de manera que en nuestro estudio de las continuas utilizaremos
este paralelo con las discretas.
DISTRIBUCIONES DE PROBABILIDADES CONTINUAS: La variable aleatoria X
será continua si los valores asignados pueden ser cualesquiera, dentro de ciertos
intervalos, es decir, puede tomar cualquier valor de R. Por ejemplo, si
consideramos el experimento aleatoria consistente en medir el peso de los
estudiantes de una universidad y tomamos la variable aleatoria X=” peso de los
estudiantes de una universidad”, esta puede tomar valores entre 30 y más
infinito. Entonces, Son aquellas donde las variables en estudio pueden asumir
cualquier valor dentro de determinados límites; por ejemplo, la estatura de un
estudiante.
DISTRIBUCIÓN UNIFORME: Se dice que una variable aleatoria continua X, que
toma todos los valores del intervalo [a, b] real, sigue una distribución uniforme de
parámetros a y b, si su función de densidad de probabilidad es:
1
f ( x)
.......si..a x b
b a
x a
F ( x) P( X x)
....si..a x b,...0....si.. a;....1...si..b x.
b a
DISTRIBUCIÓN NORMAL: Se dice que una variable aleatoria continua X, tiene
una distribución normal o de Gauss de parámetros μ y σ, si su función de
densidad de probabilidad es:
La representación gráfica así cómo los significados de la esperanza y varianza son:
DISTRIBUCIÓN EXPONENCIAL: Se dice que una variable aleatoria continua X,
tiene una distribución exponencial de parámetro β, si su función de densidad
de probabilidad es:
DENSIDAD DE UNA VARIABLE ALEATORIA CONTINÚA
FUNCIÓN DE DENSIDAD
Una función y=f(x) es una función de densidad de una variable aleatoria continua
si cumple las siguientes condiciones:
El primer hecho de importancia es que una va (variable aleatoria) continúa tiene
probabilidad cero de tomar un valor específico, sólo tiene valores positivos para
intervalos:
P( X = a ) = 0 para cualquier valor de a
Para calcular la probabilidad de que X esté en un intervalo (a, b) o (a, b] o [a, b) o
[a, b] o cualquier otro intervalo, debemos hacer uso de una función asociada a la
variable aleatoria, la función de densidad de X. Las variables aleatorias discretas
tienen la función de probabilidad, las continuas tienen función de densidad.
Además, como en el caso discreto, la función de densidad está ligada a la va X de
modo que cuando sea necesario aclarar a cuál densidad nos referimos podemos
usar la notación f x (x), poniéndole el subíndice X a la f.
PARÁMETROS DE UNA VARIABLE ALEATORIA CONTINUA
Por analogía con las definiciones de estos conceptos para variables aleatorias
discretas, se definen la esperanza matemática o media , la varianza 2 y la
desviación típica de una variable aleatoria continua de la siguiente forma:
TIPIFICACIÓN DE UNA VARIABLE ALEATORIA
Si
X
es
variable Z
una
variable
aleatoria
de
media y
desviación
típica
, la
X
tiene de media 0 y de desviación típica 1, y se llama tipificada
de X. Podemos decir que mide la desviación de X respecto de su media, tomando
como unidad la desviación típica de X.
DISTRIBUCIÓN NORMAL
Se llama distribución normal, distribución de Gauss o distribución de LaplaceGauss. Ello se debe a que el matemático francés Pierre Simon de Laplace (v.), fue
el primero que demostró la siguiente relación, muy importante en el estudio de la
distribución normal:
x2
e
Sin embargo, muchos autores consideran como auténtico descubridor de la
distribución normal a Abraham De Moivre (v.), quien publicó en 1733 un folleto
con el título de Approximatio ad summan terminorum binomii (a + b)n, en el que
aparece por primera vez la curva de la distribución de errores, que pasando el
tiempo, y con no cierta injusticia, se conoce como distribución de Gauss.
Es una de las distribuciones de probabilidad de variable continua que con más
frecuencia aparece aproximada en fenómenos reales. La gráfica de su función de
densidad tiene una forma acampanada y es simétrica respecto de un determinado
parámetro. La importancia de esta distribución radica en que permite modelar
numerosos fenómenos naturales, sociales y psicológicos.
El modelo matemático más importante en estadística es la distribución normal, ya
que provee una descripción adecuada para la distribución de una gran cantidad de
variables continuas.
Carl Friedrich Gauss.- Nació el 30 de Abril 1777 en Brunswick, (Ahora Alemania).
Falleció, el 23 de Febrero 1855 en Göttingen, Hanover (Ahora Alemania).
Cuando Gauss tenía diez años de edad, su maestro solicitó a la clase que
encontrará la suma de todos los números comprendidos entre uno y cien. El
maestro, pensando que con ello la clase estaría ocupada algún tiempo, quedó
asombrado cuando Gauss, levantó en seguida la mano y dio la respuesta correcta.
Gauss reveló que encontró la solución usando el álgebra, el maestro se dio cuenta
de que el niño era una promesa en las matemáticas. Hijo de un humilde albañil,
Gauss dio señales
de ser un genio antes de que cumpliera los tres años. A esa edad aprendió a leer y
hacer cálculos aritméticos mentales con tanta habilidad que descubrió un error en
los cálculos que hizo su padre para pagar unos sueldos. Ingresó a la escuela
primaria antes de que cumpliera los siete años. Cuando tenía doce años, criticó los
fundamentos de la geometría euclidiana; a los trece le interesaba las posibilidades
de la geometría no euclidiana. A los quince, entendía la convergencia y probó el
binomio de Newton. El genio y la precocidad de Gauss llamaron la atención del
duque de Brunswick, quien dispuso, cuando el muchacho tenía catorce años,
costear tanto su educación secundaria como universitaria. Gauss, a quien también
le interesaban los clásicos y los idiomas, pensaba que haría de la filosofía la obra
de su vida, pero las matemáticas resultaron ser una atracción irresistible.
Cuando estudiaba en Gotinga, descubrió que podría construirse un polígono
regular de diecisiete lados usando sólo la regla y el compás. Enseñó la prueba a su
profesor, quién se demostró un tanto escéptico y le dijo que lo que sugería era
imposible; pero Gauss demostró que tenía la razón. El profesor, no pudiendo
negar lo evidente, afirmó que también él procedió de la misma manera. Sin
embargo, se reconoció el mérito de Gauss, y la fecha de su descubrimiento, 30 de
Marzo de 1796, fue importante en la historia de las matemáticas. Posteriormente,
Gauss encontró la fórmula para construir los demás polígonos regulares con la
regla y el compás.
A la edad de setenta y siete años, Gauss falleció. Se ha dicho que la lápida que
señala su tumba fue escrita con un diagrama, que construyó el mismo Gauss, de
un polígono de diecisiete lados. Durante su vida, se reconoció que era el
matemático más grande de los siglos XVIII y XIX. Su obra en las matemáticas
contribuyó a formar una base para encontrar la solución de problemas
complicadísimos de las ciencias físicas y naturales.
La distribución normal es en forma de campana, habitualmente llamada
distribución de Gauss. Es simétrica en torno a su media ( ); la media, mediana y
modo son iguales; el área total de la curva por encima del eje basal x es la unidad
del área = 1, por lo tanto cada sector de derecha e izquierda tiene un valor de 0,5.
Si se trazan líneas perpendiculares a un desvío estándar ( ) de distancia de la
media, se obtiene un 68% del área de la curva. Dos desvíos estándar encierran un
95% y tres un 99,7% de la curva. La mayoría de las variables aleatorias que se
presentan en los estudios relacionados con las ciencias sociales, Administración,
físicas y biológicas, por ejemplo, el peso de niños recién nacidos, talla de jóvenes
de 18 años en una determinada región, son continuas y se distribuyen según una
función de densidad.
Esta distribución es frecuentemente utilizada en las aplicaciones estadísticas. Es
propio que ciertos fenómenos tienden a parecerse en su comportamiento a esta
distribución. Muchas variables aleatorias continuas presentan una función de
densidad cuya gráfica tiene forma de campana.
En otras ocasiones, al considerar distribuciones binomiales, tipo B(n, p), para un
mismo valor de p y valores de n cada vez mayores, se ve que sus polígonos de
frecuencias se aproximan a una curva en "forma de campana".
En resumen, la importancia de la distribución normal se debe principalmente a que
hay muchas variables asociadas a fenómenos naturales que siguen el modelo de la
normal.
Caracteres morfológicos de individuos (personas, animales, plantas,...) de
una especie, p.ejm. tallas, pesos, envergaduras, diámetros, perímetros,...
Caracteres fisiológicos, por ejemplo: efecto de una misma dosis de un
fármaco, o de una misma cantidad de abono.
Caracteres sociológicos, por ejemplo: consumo de cierto producto por un
mismo grupo de individuos, puntuaciones de examen.
Caracteres psicológicos,
adaptación a un medio,...
por
ejemplo:
cociente
intelectual,
grado
de
Errores cometidos al medir ciertas magnitudes.
Valores estadísticos muestrales, por ejemplo : la media.
Otras distribuciones como la binomial o la de Poisson son aproximaciones
normales, ...
Y en general cualquier característica que se obtenga como suma de muchos
factores.
En el gráfico se observa la campana de Gauss, representante de la distribución
normal y sus desvíos estándares.
Sir Francis Galton construyó un ingenioso dispositivo que permitía obtener de
forma experimental la curva de distribución normal. La mayoría de las
magnitudes, incluida la inteligencia, se distribuyen siguiendo esta ley normal, que
matemáticamente viene expresada por la función:
Donde:
e es la constante 2,7182…(base de los logaritmos neperianos).
es 3,1415… (Relación entre la longitud de la circunferencia y su diámetro).
x es la abscisa, cualquier punto del intervalo.
es la media de la variable aleatoria.
es la desviación tipo de la variable aleatoria,
2 es la varianza de la variable aleatoria
f(x) la ordenada de la curva.
Dicha curva y tal como vemos en la gráfica, presenta un apiñamiento de
frecuencias altas en torno a la media, que se alejan de la misma a medida que
ganan en singularidad.La medida de la distancia al valor central es indicado por la
desviación tipo o estándar.
Ejemplos de distribuciones normales con diferentes parámetros
Se dice que una variable aleatoria continua X sigue una distribución normal de
parámetros μ y σ y se denota X~N (μ, σ) si su función de densidad está dada
por:
Donde μ (mu) es la media y σ (sigma) es la desviación estándar (σ2 es la
varianza). Se llama distribución normal "estándar" a aquélla en la que sus
parámetros toman los valores μ = 0 y σ = 1.
Como e y π son constantes, la forma de la curva normal depende solamente de los
dos parámetros de la distribución normal, la media μx y la desviación estándar σx.
Las diferentes curvas normales van a variar dependiendo de esos dos parámetros.
En matemáticas, la ecuación de la distribución normal se puede representar
visualmente como una curva en forma de campana. El área debajo de esta curva
se halla por medio del integral de la función y corresponde al porciento o la
proporción de puntuaciones que se encuentran en el intervalo dado.
La distribución normal queda definida por dos parámetros, su media y su
desviación típica y la representamos así N ( , ) . Para cada valor de y se
tendrá una
función de densidad diferente, por lo tanto la expresión N ( , )
representa una familia de distribuciones normales.
Donde μ es la media de la variable aleatoria y σ es su desviación típica. Este tipo
de variables se dice que se distribuye normalmente. El área bajo la función de
densidad es 1. La función de densidad, en el caso de la distribución Normal, tiene
forma de campana:
Para una variable aleatoria X, que se distribuya normalmente con media: μ y
desviación típica: σ, la probabilidad de que la variable X esté comprendida entre
los valores a y b es el área teñida de rojo en la siguiente figura:
PROPIEDADES DE LA DISTRIBUCIÓN NORMAL
1.- Tiene una única moda, que coincide con su media y su mediana.
2.- La curva normal es asintótica al eje de abscisas. Por ello, cualquier valor entre
y es teóricamente posible. El área total bajo la curva es, por tanto, igual
a 1.
3.- Es simétrica con respecto a su media . Según esto, para este tipo de
variables existe una probabilidad de un 50% de observar un dato mayor que la
media, y un 50% de observar un dato menor.
4.- La distancia entre la línea trazada en la media y el punto de inflexión de la
curva es igual a una desviación típica ( ). Cuanto mayor sea , más aplanada
será la curva de la densidad.
5.- El área bajo la curva comprendida entre los valores situados aproximadamente
a dos desviaciones estándar de la media es igual a 0.95. En concreto, existe un
95% de posibilidades de observar un valor comprendido en el intervalo
1.96; 1.96 .
6.- La forma de la campana de Gauss depende de los parámetros y . La
media indica la posición de la campana, de modo que para diferentes valores de
la gráfica es desplazada a lo largo del eje horizontal. Por otra parte, la desviación
estándar determina el grado de apuntamiento de la curva. Cuanto mayor sea el
valor de , más se dispersarán los datos en torno a la media y la curva será más
plana. Un valor pequeño de este parámetro indica, por tanto, una gran
probabilidad de obtener datos cercanos al valor medio de la distribución.
7.- Como se deduce de este último apartado, no existe una única distribución
normal, sino una familia de distribuciones con una forma común, diferenciadas por
los valores de su media y su varianza. De entre todas ellas, la más utilizada es la
distribución normal estándar, que corresponde a una distribución de media 0 y
varianza 1.
8.- Ql y Q3 están situados a 2/3 de una desviación estándar. El 68 % del área de la
curva (probabilidad) se encuentra a una desviación estándar de la media.
9.- La variable tiene un alcance infinito, pero la mayor parte del área bajo la curva
se encuentra a tres desviaciones estándar de la media.
FUNCIÓN DE DISTRIBUCIÓN
Puede tomar cualquier valor (- , + )
Son más probables los valores cercanos a uno central que llamamos media
Conforme nos separamos de ese valor , la probabilidad va decreciendo de igual
forma a derecha e izquierda (es simétrica).
F(x) es el área sombreada de esta gráfica
LA DISTRIBUCIÓN NORMAL ESTANDARIZADA O TIPIFICACIÓN
La Distribución Normal Estándar es una Distribución Normal teórica que utiliza un
sistema numérico común. Cuando se estudia la variable de peso de los niños al
nacer, o el grueso de tornillos, o el número de frutos dañados en un árbol, aun
cuando las distribuciones de datos muestren la misma forma, las unidades
métricas son variables, por tanto, para poderlas comparar con una distribución
patrón es necesario referirlas en la misma unidad de medida. Esta unidad de
medida es la desviación estándar (se verá más adelante), de esta manera, sean
pesos de bebes, grueso de tornillos o frutos de árboles, transformados a una
unidad estándar, estaremos hablando en la misma escala. Cuando se diga por
ejemplo, entre el punto A y el punto B hay k desviaciones estándar, sin importar
las unidades en que fueron medidos los datos, kilos, micras o unidades para el
ejemplo. Por tanto, al comparar las magnitudes entre el punto A y el punto B en
los tres análisis con las unidades de la Distribución Normal Estándar, se podrá
deducir entre otras cosas, la magnitud relativa entre el punto A y el punto B. Debe
quedar claro que las comparaciones únicamente son posibles en poblaciones
similares, niños con niños, tornillos con tornillos etc.
Puesto que hay un número infinito de combinaciones para los dos parámetros,
hay un número infinito de curvas normales diferentes. Este problema se ha
resuelto prácticamente al transformar los valores de todas las distribuciones
normales a los valores de una distribución normal estandarizada (tipificada)
representada por la curva normal estandarizada.
Las puntuaciones estandarizadas (tipificadas) se logran restando la media a cada
observación y dividiendo entre la desviación estándar. La unidad estándar o
tipificada se llama Z y se obtiene mediante la fórmula:
Z
x
Donde μ es la media de la distribución y σ su desviación estándar.
En muchas ocasiones se quieren comparar puntuaciones que pertenecen a dos
distribuciones normales diferentes. La diferencia entre las dos distribuciones radica
en que las medias y las desviaciones estándar no son iguales. Sin embargo la
comparación se hace posible si se convierten las puntuaciones de ambas
distribuciones a puntuaciones z que corresponden a la distribución normal
estandarizada o tipificada.
Por tanto su función de densidad es
y su función de distribución es
Siendo la representación gráfica de esta función la siguiente:
A la variable Z se la denomina variable tipificada de X, y a la curva de su función
de densidad curva normal tipificada.
CARACTERÍSTICA DE LA DISTRIBUCIÓN NORMAL TIPIFICADA
(REDUCIDA O ESTÁNDAR)
No depende de ningún parámetro
Su media es 0, su varianza es 1 y su desviación típica es 1.
La curva f(x) es simétrica respecto del eje 0Y
Tiene un máximo en el eje Y
Tiene dos puntos de inflexión en z =1 y z = -1
La curva normal estándar tiene = 0 y = 1. Recordamos que la probabilidad
equivale al área bajo la curva, que el área bajo toda la curva es 1 y que el área
bajo cada mitad de la curva es 0.5. Para calcular probabilidades en una curva
normal no estándar, usamos la fórmula de conversión z. Cuando la media de la
distribución normal es 0 y la varianza es 1 se denomina "normal tipificada", y su
ventaja reside en que hay tablas donde se recoge la probabilidad acumulada para
cada punto de la curva de esta distribución.
Ejemplo:
Consideremos que el peso de los niños varones venezolanos en el momento del
nacimiento se distribuyen normalmente. Si sabemos que el peso medio en el
momento de nacer son 3,25 Kg. y la desviación típica es de 0,82 Kg., ¿cuál es la
probabilidad de que el peso de un niño varón al nacer sea superior a 4 Kg?
Z
X 4 3.25
0.9146
0.82
Tipificamos la variable aleatoria X, peso de los niños al nacer. En el proceso de
tipificación, al valor de X = 4, le corresponde el valor, t = 0,9146:
En la tabla de la distribución normal tipificada, buscamos el valor de α
correspondiente al valor de t = 0,9146 ; la probabilidad de t > 0,9146 es, según
se puede apreciar en la figura:
. Luego:
2
Por lo tanto la probabilidad de que un niño al nacer tenga un peso superior a 4 kg.
es de 18.0 %.
EJEMPLOS:
A) Calcular P (z < –1.35) y P (z > –1.35). Solución: abajo se reproduce parte
de la tabla:
B)
z
.00
.01
.02
.03
.04
.05
.06
.07
.08
.09
–1.3
.0968
.0951
.0934
.0918
.0901
.0885
.0869
.0853
.0838
.0823
Recordamos que la tabla proporciona el área bajo la curva a la izquierda de z. Por
lo tanto,
P (z < –1.35) = 0.0885.
La otra área se obtiene así: P (z > –1.35) = 1 – 0.0885 = 0.9115.
C) Una distribución
63).
D)
Solución: Primero transformamos el valor de x a su equivalente en z: z = (63–
60)/5 = 0.6.
z
.00
.01
.02
.03
.04
.05
.06
.07
.08
.09
0.6
.7257
.7291
.7324
.7357
.7389
.7422
.7454
.7486
.7517
.7549
Al consultar la tabla (ver arriba): P(x < 63) = P(z < 0.60) = 0.7257.
Además, P(x > 63) = P (z > 0.60) = 1 – P (z < 0.60) = 0.2743.
EJERCICIOS: Calcular las siguientes probabilidades.
1)
2)
3)
4)
P(z
P(z
P(z
P(z
>
<
>
<
–2.43)
–0.96)
1.17)
2.39)
5) Si = 110 y = 4, calcular P(x < 107) y P(x > 105)
6) Si = 30 y = 2, calcular P(x < 31.2) y P(x > 32.3)
Consideremos, el siguiente problema:
Supongamos que se sabe que el peso de los sujetos de una determinada
población sigue una distribución aproximadamente normal, con una media de 80
Kg. y una desviación estándar de 10 Kg. ¿Podremos saber cuál es la probabilidad
de que una persona, elegida al azar, tenga un peso superior a 100 Kg?
SOLUCIÓN: Expresando por X a la variable que representa el peso de los
individuos en esa población, ésta sigue una distribución N (80, 10).
Su
distribución no es de la normal estándar, entonces, es útil transformar esta
característica según la Ecuación siguiente:
Así, la probabilidad que se desea calcular será:
Como el área total bajo la curva es igual a 1, se puede deducir que:
Esta última probabilidad puede ser fácilmente obtenida a partir de la tabla,
resultando ser
. Por lo tanto, la probabilidad buscada de que una
persona elegida aleatoriamente de esa población tenga un peso mayor de 100 Kg.,
es de:
1–0.9772 = 0.0228, es decir, aproximadamente de un 2.3%.
De modo análogo, podemos obtener la probabilidad de que el peso de un sujeto
esté entre 60 y 100 Kg:
Tomando a = -2 y b = 2, podemos deducir que:
Por el ejemplo anterior, se sabe que P( z 2 ) 0.9772 . Para la segunda
probabilidad, sin embargo, encontramos el problema de que las tablas estándar no
P( z 2 ) para valores negativos de la variable. Sin
proporcionan el valor de
embargo, haciendo uso de la simetría de la distribución normal, se tiene que:
Finalmente, la probabilidad buscada de que una persona elegida al azar tenga un
peso entre 60 y 100 Kg., es de 0.9772-0.0228=0.9544, es decir,
aproximadamente de un 95%. Resulta interesante comprobar que se obtendría la
misma conclusión recurriendo a la propiedad de la distribución normal.
No obstante, es fácil observar que este tipo de situaciones no corresponde a lo que
habitualmente nos encontramos en la práctica. Generalmente no se dispone de
información acerca de la distribución teórica de la población, sino que más bien el
problema se plantea a la inversa: a partir de una muestra extraída al azar de la
población que se desea estudiar, se realizan una serie de mediciones y se desea
extrapolar los resultados obtenidos a la población de origen.
EJEMPLO: Supongamos que se dispone del peso de n =100 individuos de esa
misma población, obteniéndose una media muestral de X 75 Kg., y una
desviación estándar muestral S 12 Kg., se pretende extraer alguna conclusión
acerca del valor medio real de ese peso en la población original.
La solución a este tipo de cuestiones se basa en un resultado elemental de la
teoría estadística, el llamado teorema central del límite. Dicho axioma viene a
decirnos que las medias de muestras aleatorias de cualquier variable siguen ellas
mismas una distribución normal con igual media que la de la población y
desviación estándar la de la población dividida por
n . En nuestro caso,
podremos entonces considerar la media muestral X N ,
n
, con lo cual, a
partir de la propiedad de la normal se conoce que aproximadamente un 95% de
los posibles valores de X caerían dentro del intervalo
1.96
1.96
;
n
n
.
Puesto que los valores de y son desconocidos, podríamos pensar en
aproximarlos por sus análogos muestrales, resultando
.
Estaremos, por lo tanto, un 95% seguros de que el peso medio real en la
población de origen oscila entre 75.6 Kg y 80.3 Kg. Aunque la teoría estadística
subyacente es mucho más compleja, en líneas generales éste es el modo de
construir un intervalo de confianza para la media de una población.
EJEMPLO: Supongamos que cierto fenómeno pueda ser representado mediante
una va X N ( 45 ,81 ) , y queremos calcular la probabilidad de que X tome un valor
entre 39 y 48, es decir,
P39 X 48 ??
SOLUCIÓN: Comenzamos haciendo el cambio de variable
Z
X X 45 X 45
. De modo que
9
81
P39 X 48 0.378 37.80%.
Tabla de Áreas bajo la curva normal estándar. Los valores de la tabla que
no se muestran en negrita representan la probabilidad de observar un
valor menor o igual a z. La cifra entera y el primer decimal de z se buscan
en la primera columna, y el segundo decimal en la cabecera de la tabla.
z
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
3.0
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
0.00
0.5000
0.5398
0.5793
0.6179
0.6554
0.6915
0.7257
0.7580
0.7881
0.8159
0.8413
0.8643
0.8849
0.9032
0.9192
0.9332
0.9452
0.9554
0.9641
0.9713
0.9772
0.9821
0.9861
0.9893
0.9918
0.9938
0.9953
0.9965
0.9974
0.9981
0.9987
0.9990
0.9993
0.9995
0.9997
0.9998
0.9998
0.9999
0.9999
1.0000
0.01
0.5040
0.5438
0.5832
0.6217
0.6591
0.6950
0.7291
0.7611
0.7910
0.8186
0.8438
0.8665
0.8869
0.9049
0.9207
0.9345
0.9463
0.9564
0.9649
0.9719
0.9778
0.9826
0.9864
0.9896
0.9920
0.9940
0.9955
0.9966
0.9975
0.9982
0.9987
0.9991
0.9993
0.9995
0.9997
0.9998
0.9998
0.9999
0.9999
1.0000
0.02
0.5080
0.5478
0.5871
0.6255
0.6628
0.6985
0.7324
0.7642
0.7939
0.8212
0.8461
0.8686
0.8888
0.9066
0.9222
0.9357
0.9474
0.9573
0.9656
0.9726
0.9783
0.9830
0.9868
0.9898
0.9922
0.9941
0.9956
0.9967
0.9976
0.9982
0.9987
0.9991
0.9994
0.9995
0.9997
0.9998
0.9999
0.9999
0.9999
1.0000
0.03
0.5120
0.5517
0.5910
0.6293
0.6664
0.7019
0.7357
0.7673
0.7967
0.8238
0.8485
0.8708
0.8907
0.9082
0.9236
0.9370
0.9484
0.9582
0.9664
0.9732
0.9788
0.9834
0.9871
0.9901
0.9925
0.9943
0.9957
0.9968
0.9977
0.9983
0.9988
0.9991
0.9994
0.9996
0.9997
0.9998
0.9999
0.9999
0.9999
1.0000
0.04
0.5160
0.5557
0.5948
0.6331
0.6700
0.7054
0.7389
0.7704
0.7995
0.8264
0.8508
0.8729
0.8925
0.9099
0.9251
0.9382
0.9495
0.9591
0.9671
0.9738
0.9793
0.9838
0.9875
0.9904
0.9927
0.9945
0.9959
0.9969
0.9977
0.9984
0.9988
0.9992
0.9994
0.9996
0.9997
0.9998
0.9999
0.9999
0.9999
1.0000
0.05
0.5199
0.5596
0.5987
0.6368
0.6736
0.7088
0.7422
0.7734
0.8023
0.8289
0.8531
0.8749
0.8944
0.9115
0.9265
0.9394
0.9505
0.9599
0.9678
0.9744
0.9798
0.9842
0.9878
0.9906
0.9929
0.9946
0.9960
0.9970
0.9978
0.9984
0.9989
0.9992
0.9994
0.9996
0.9997
0.9998
0.9999
0.9999
0.9999
1.0000
0.06
0.5239
0.5636
0.6026
0.6406
0.6772
0.7123
0.7454
0.7764
0.8051
0.8315
0.8554
0.8770
0.8962
0.9131
0.9279
0.9406
0.9515
0.9608
0.9686
0.9750
0.9803
0.9846
0.9881
0.9909
0.9931
0.9948
0.9961
0.9971
0.9979
0.9985
0.9989
0.9992
0.9994
0.9996
0.9997
0.9998
0.9999
0.9999
0.9999
1.0000
0.07
0.5279
0.5675
0.6064
0.6443
0.6808
0.7157
0.7486
0.7794
0.8078
0.8340
0.8577
0.8790
0.8980
0.9147
0.9292
0.9418
0.9525
0.9616
0.9693
0.9756
0.9808
0.9850
0.9884
0.9911
0.9932
0.9949
0.9962
0.9972
0.9979
0.9985
0.9989
0.9992
0.9995
0.9996
0.9997
0.9998
0.9999
0.9999
0.9999
1.0000
0.08
0.5319
0.5714
0.6103
0.6480
0.6844
0.7190
0.7517
0.7823
0.8106
0.8365
0.8599
0.8810
0.8997
0.9162
0.9306
0.9429
0.9535
0.9625
0.9699
0.9761
0.9812
0.9854
0.9887
0.9913
0.9934
0.9951
0.9963
0.9973
0.9980
0.9986
0.9990
0.9993
0.9995
0.9996
0.9997
0.9998
0.9999
0.9999
0.9999
1.0000
0.09
0.5359
0.5753
0.6141
0.6517
0.6879
0.7224
0.7549
0.7852
0.8133
0.8389
0.8621
0.8830
0.9015
0.9177
0.9319
0.9441
0.9545
0.9633
0.9706
0.9767
0.9817
0.9857
0.9890
0.9916
0.9936
0.9952
0.9964
0.9974
0.9981
0.9986
0.9990
0.9993
0.9995
0.9997
0.9998
0.9998
0.9999
0.9999
0.9999
1.0000
¿CÓMO SE LEE ESTA TABLA?
La columna de la izquierda indica el valor cuya probabilidad acumulada queremos
conocer. La primera fila nos indica el segundo decimal del valor que estamos
consultando.
EJEMPLO: queremos conocer la probabilidad acumulada en el valor 2,75.
Entonces buscamos en la columna de la izquierda el valor 2,7 y en la primera fila
el valor 0,05. La casilla en la que se interseccionan es su probabilidad acumulada
(0,99702, es decir 99.7%).
ATENCIÓN: la tabla nos da la probabilidad acumulada, es decir, la que va desde
el inicio de la curva por la izquierda hasta dicho valor. No nos da la probabilidad
concreta en ese punto. En una distribución continua en el que la variable puede
tomar infinitos valores, la probabilidad en un punto concreto es prácticamente
despreciable.
EJEMPLO: Imaginemos que una variable continua puede tomar valores entre 0 y
5. La probabilidad de que tome exactamente el valor 2 es despreciable, ya que
podría tomar infinitos valores: por ejemplo: 1,99, 1,994, 1,9967, 1,9998,
1999791, etc.
Veamos otros ejemplos:
Probabilidad acumulada
Probabilidad acumulada
Probabilidad acumulada
Veamos ahora, como
normal:
en el valor 0,67: la
en el valor 1,35: la
en el valor 2,19: la
podemos utilizar
respuesta es 0,7486
respuesta es 0,9115
respuesta es 0,98574
esta tabla con una distribución
EJEMPLO: el salario medio anual de los empleados de una empresa se distribuye
según una distribución normal, con media 5 millones de Bs. y desviación típica 1
millón de Bs. Calcular el porcentaje de empleados con un sueldo inferior a 7
millones de Bs.
Lo primero que haremos es transformar esa distribución en una normal tipificada,
para ello se crea una nueva variable (Z) que será igual a la anterior (X) menos su
media y dividida por la desviación típica
Z
X
En el ejemplo, la nueva variable sería:
Z
X 5
1
Esta nueva variable se distribuye como una normal tipificada. La variable Z que
corresponde a una variable X de valor 7 es:
Z
75
2
1
Ya podemos consultar en la tabla la probabilidad acumulada para el valor 2
(equivalente a la probabilidad de sueldos inferiores a 7 millones de Bs.). Esta
probabilidad es 0,97725
Por lo tanto, el porcentaje de empleados con salarios inferiores a 7 millones de Bs.
es del 97,725%.
EJERCICIO 1º: La renta media de los habitantes de un pueblo es de 4 millones
de Bs/año, con una varianza de 1,5. Se supone que se distribuye según una
distribución normal. Calcular:
a) Porcentaje de la población con una renta inferior a 3 millones de Bs.
b) Renta a partir de la cual se sitúa el 10% de la población con mayores ingresos.
c) Ingresos mínimo y máximo que engloba al 60% de la población con renta
media.
a) Porcentaje de la población con una renta inferior a 3 millones de Bs.
SOLUCIÓN:
Lo primero que tenemos que hacer es calcular la normal tipificada:
Z
X 4
1.22
Recuede que el denominador es la desviación típica (raíz cuadrada de la varianza)
El valor de Z equivalente a 3 millones de Bs. es – 0,816.
P (X < 3) = P (Z < – 0,816)
Ahora tenemos que ver cuál es la probabilidad acumulada hasta ese valor.
Tenemos un problema: la tabla de probabilidades sólo abarca valores positivos,
no obstante, este problema tiene fácil solución, ya que la distribución normal es
simétrica respecto al valor medio.
Por lo tanto:
P (Z < – 0,816) = P (Z > 0,816)
Por otra parte, la probabilidad que hay a partir de un valor es igual a 1 (100%)
menos la probabilidad acumulada hasta dicho valor:
P (Z > 0,816) = 1 - P (Z < 0,816) = 1 - 0,7925 (aprox.) = 0,2075
Luego, el 20,75% de la población tiene una renta inferior a 3 millones Bs.
b) Nivel de ingresos a partir del cual se sitúa el 10% de la población con
renta más elevada.
Vemos en la tabla el valor de la variable tipificada cuya probabilidad acumulada es
el 0,9 (90%), lo que quiere decir que por encima se sitúa el 10% superior.
Ese valor corresponde a Z = 1,282 (aprox.). Ahora calculamos la variable normal
X equivalente a ese valor de la normal tipificada:
1,282
X 4
1.282( 1.22 ) X 4 X 1.57 4 X 5.57 .
1.22
Despejando X, su valor es 5,57. Por lo tanto, aquellas personas con ingresos
superiores a 5,57 millones de Bs. constituyen el 10% de la población con renta
más elevada.
c) Nivel de ingresos mínimo y máximo que engloba al 60% de la población
con renta media
Vemos en la tabla el valor de la variable normalizada Z cuya probabilidad
acumulada es el 0,8 (80%). Como sabemos que hasta la media la probabilidad
acumulada es del 50%, quiere decir que entre la media y este valor de Z hay un
30% de probabilidad.
Por otra parte, al ser la distribución normal simétrica, entre -Z y la media hay otro
30% de probabilidad. En definitiva, el segmento (-Z, Z) engloba al 60% de
población con renta media.
El valor de Z que acumula el 80% de la probabilidad es 0,842 (aprox.), por lo que
el segmento viene definido por (-0,842, + 0,842). Ahora calculamos los valores de
la variable X correspondientes a estos valores de Z.
Los valores de X son 2,97 y 5,03. Por lo tanto, las personas con ingresos
superiores a 2,97 millones de Bs. e inferiores a 5,03 millones de Bs. constituyen el
60% de la población con un nivel medio de renta.
EJERCICIO 2º: La vida media de los habitantes de un país es de 68 años, con
una varianza de 25. Se hace un estudio en una pequeña ciudad de 10.000
habitantes:
a) ¿Cuántas personas superarán posiblemente los 75 años?
b)
c) ¿Cuántos vivirán menos de 60 años?
d)
SOLUCIÓN:
a) Personas que vivirán (posiblemente) más de 75 años
b)
Calculamos el valor de la normal tipificada equivalente a 75 años
Z
75 68
1.4
5
Por lo tanto
P (X > 75) = (Z > 1,4) = 1 - P (Z < 1,4) = 1 - 0,9192 = 0,0808
Luego, el 8,08% de la población (808 habitantes) vivirán más de 75 años.
c) Personas que vivirán (posiblemente) menos de 60 años
d)
Calculamos el valor de la normal tipificada equivalente a 60 años
Z
60 68
1,6 . Por lo tanto P (X < 60) = (Z < -1,6) = P (Z > 1,6) = 1 - P (Z <
5
1,6) = 0,0548.
Luego, el 5,48% de la población (548 habitantes) no llegarán probablemente a
esta edad.
EJERCICIO 3: El consumo medio anual de cerveza de los habitantes de una país
es de 59 litros, con una varianza de 36. Se supone que se distribuye según una
distribución normal.
a) Si usted presume de buen bebedor, ¿cuántos litros de cerveza tendría que
beber al año para pertenecer al 5% de la población que más bebe?.
b)
c) Si usted bebe 45 litros de cerveza al año y su mujer le califica de borracho
¿qué podría argumentar en su defensa?
d)
a) 5% de la población que más bebe.
b)
Vemos en la tabla el valor de la variable tipificada cuya probabilidad acumulada es
el 0,95 (95%), por lo que por arriba estaría el 5% restante.
Ese valor corresponde a Z = 1,645 (aprox.). Ahora calculamos la variable normal
X equivalente a ese valor de la normal tipificada:
X 58
6( 1,645 ) X 58 X 9.87 58
6
X 67 ,87
1,645
Despejando X, su valor es 67,87. Por lo tanto, tendría usted que beber más de
67,87 litros al año para pertenecer a ese "selecto" club de grandes bebedores de
cerveza.
b) Usted bebe 45 litros de cerveza al año. ¿Es usted un borracho?
Vamos a ver en que nivel de la población se situaría usted en función de los litros
de cerveza consumidos.
Calculamos el valor de la normal tipificada correspondiente a 45 litros:
Z
45 58
2,2
6
Por lo tanto
P (X < 45) = (Z < -2,2) = P (Z> 2,2) = 1 - P (Z < 2,2) = 0,0139
Luego, tan sólo un 1,39% de la población bebe menos que usted. Parece un
argumento de suficiente peso para que dejen de catalogarle de "enamorado de la
bebida"
EJERCICIO 4: A un examen de oposición se han presentado 2.000 aspirantes. La
nota media ha sido un 5,5, con una varianza de 1,1.
a) Tan sólo hay 100 plazas. Usted ha obtenido un 7,7. ¿Sería oportuno ir
organizando una fiesta para celebrar su éxito?
b)
b) Va a haber una 2ª oportunidad para el 20% de notas más altas que no se
hayan clasificados. ¿A partir de que nota se podrá participar en este "Nuevo
Ingreso"?
a) Ha obtenido usted un 7,7
b)
Vamos a ver con ese 7,7 en que nivel porcentual se ha situado usted, para ello
vamos a comenzar por calcular el valor de la normal tipificada equivalente.
Z
7.7 5.5
2.1 . A este valor de Z le corresponde una probabilidad acumulada
1,049
(ver tablas) de 0,98214 (98,214%), lo que quiere decir que por encima de usted
tan sólo se encuentra un 1,786%.
Si se han presentado 2.000 aspirante, ese 1,786% equivale a unos 36 aspirantes;
como hay 100 plazas disponibles, tiene usted suficientes probabilidades como para
ir organizando la "mejor de las fiestas".
b) "Repesca" para el 20% de los candidatos
Vemos en la tabla el valor de la normal tipificada que acumula el 80% de la
probabilidad, ya que por arriba sólo quedaría el 20% restante.
Este valor de Z corresponde a 0,842 (aprox.). Ahora calculamos el valor de la
normal X equivalente:
X 5.5
( 0.842 )(1,049 ) X 5.5 X ( 0,883 ) 5.5
1,049
X 6,38
0,842
Despejamos la X, su valor es 6,38. Por lo tanto, esta es la nota a partir de la cual
se podrá acudir al "Nuevo Ingreso".
LA DISTRIBUCIÓN "T DE STUDENT":
La distribución t (de Student) es una distribución
de probabilidad que florece
del problema de estimar la media de una población normalmente distribuida
cuando el tamaño de la muestra es pequeño. Aparece de manera natural al
realizar la prueba t de Student para la determinación de las diferencias entre dos
medias muestrales y para la construcción del intervalo de confianza para la
diferencia entre las medias de dos poblaciones cuando se desconoce la desviación
típica de una población y ésta debe ser estimada a partir de los datos de una
muestra. La distribución t de Student es la distribución de probabilidad del
Z
cociente
donde, Z tiene una distribución normal de media nula y varianza 1;
V
v
V tiene una distribución chi-cuadrado con
grados de libertad; Z y V son
Z
independientes. Si μ es una constante no nula, el cociente
es una
V
v
variable aleatoria que sigue la distribución t de Student no central con parámetro
de no-centralidad μ.
En la mayoría de casos reales o prácticos es frecuente que el tamaño de la
muestra sea limitado por el costo y por el tiempo por el cual se requiere de
procedimientos un poco diferentes a los utilizados para muestras grandes o
mayores que treinta observaciones que por lo general se asocian con la
distribución normal. Los procedimientos de estimación y prueba de hipótesis para
muestras pequeñas como es el caso de este trabajo son tratados
preferencialmente por la distribución denominada "T de student", Descubierta por
William S Gosset y publicada en 1908 bajo el seudónimo de "student", otra
característica que permite utilizar una distribución "T" es que la desviación
estándar de tipo poblacional se desconoce y se debe utilizar una desviación
estándar de tipo muestral; ésta también es una razón para utilizar la "T de
Student" .
Las muestras de tamaño N>30, se les llamadas grandes muestras, las
distribuciones de muestreo de muchos estadísticos son aproximadamente
normales, siendo la aproximación tanto mejor cuanto mayor sea N. Para muestras
de tamaño menor que 30, llamadas pequeñas muestras, esa aproximación no es
adecuada y empeora al decrecer N, de modo que son precisas ciertas
modificaciones. El estudio de la distribución de muestreo de los estadísticos para
pequeñas muestras se llama teoría de pequeñas muestras. Sin embargo, un
nombre más apropiado sería teoría exacta del muestreo, pues sus resultados son
válidos tanto para pequeñas muestras como para grandes. En esta guía
analizaremos la Distribución de Student, la cual se designa con la letra t.
Definamos el estadístico
dado por Z
t
X ( X )
N que es análogo al estadístico z
S
S
N
X X
N.
N
INTERVALOS DE CONFIANZA
Al igual que se hizo con la distribución normal, se pueden definir los intervalos de
confianza 95%, 99%, u otros, usando la tabla de la distribución t. De esta forma
podemos estimar la media de la población dentro de los límites especificados.
X t
2
S
, Donde S
es la desviación estándar estimada de X .
N
N
GRADOS DE LIBERTAD
Para el cálculo de un estadístico tal como t y
es necesario emplear tanto
observaciones de muestras como propiedades de ciertos parámetros de la
población, si estos parámetros son desconocidos, hay que estimarlos a partir de la
muestra.
¿Qué son los grados de libertad? Se pueden definir como el número de valores
que se pueden escoger libremente.
Suponiendo que se está trabajando con dos valores de muestra, a y b, y se sabe
que tienen una media de 18. Simbólicamente, se puede expresar:
ab
18 a b 36 . ¿Cómo se puede encontrar los valores que a y b puedan
2
tomar en esta situación? La respuesta es que a y b pueden ser cualquiera de dos
valores cuya suma sea 36, ya que 36 entre 2 es 18.
Suponiendo que a tiene un valor de 10; ahora b ya no está libre de tomar
cualquier valor, sino que debe tomar solamente el valor 26 puesto que, si a = 10,
entonces 10 + b = 36, por lo tanto b = 26.
Este ejemplo demuestra que cuando existen 2 elementos de una muestra y solo
conocemos la media de la muestra de esos elementos, entonces somos libres de
especificar solamente uno de esos elementos, puesto que el otro estará
determinado por el hecho de que los 2 elementos suman el doble de la mitad de la
muestra. En términos estadísticos se dice que tenemos un grado de libertad.
Observemos otro ejemplo. Existen 7 elementos en una muestra y se sabe que la
media de estos elementos es 16. Simbólicamente se tiene la siguiente situación:
abcd e f g
16
7
En este caso, los grados de libertad (GL) o el número de variables que se pueden
especificar libremente es 7 – 1 = 6. Se tiene la libertad de asignar valores a 6
variables, y luego ya no tenemos libertad de especificar el valor de la séptima
variable, puesto que esa queda determinada automáticamente. En cada uno de los
ejemplo tenemos un grado de libertad que es igual a n – 1 grados de libertad,
suponiendo que n es el tamaño de la muestra. Utilizamos los grados de liberta
cuando se elige una distribución t para estimar una media de población, y se
utilizará n – 1 GL, tomando n igual al tamaño de la muestra.
Regiones de aceptación y rechazo en el contraste de hipótesis
Distribución t de Student para varios valores
Valores críticos para la distribución Student's - t
alfa = área a la derecha de t(df, alfa)
T~t(df)
P(T>t(df,alfa))
grados alfa
de
libertad 0.1000 0.0500 0.0250 0.0100 0.0050 0.0010 0.0005
1
3.078
6.314
12.706 31.821 63.656 318.289 636.578
2
1.886
2.920
4.303
6.965
9.925
22.328
31.600
3
1.638
2.353
3.182
4.541
5.841
10.214
12.924
4
1.533
2.132
2.776
3.747
4.604
7.173
8.610
5
1.476
2.015
2.571
3.365
4.032
5.894
6.869
6
1.440
1.943
2.447
3.143
3.707
5.208
5.959
7
1.415
1.895
2.365
2.998
3.499
4.785
5.408
8
1.397
1.860
2.306
2.896
3.355
4.501
5.041
9
1.383
1.833
2.262
2.821
3.250
4.297
4.781
10
1.372
1.812
2.228
2.764
3.169
4.144
4.587
11
1.363
1.796
2.201
2.718
3.106
4.025
4.437
12
1.356
1.782
2.179
2.681
3.055
3.930
4.318
13
1.350
1.771
2.160
2.650
3.012
3.852
4.221
14
1.345
1.761
2.145
2.624
2.977
3.787
4.140
15
1.341
1.753
2.131
2.602
2.947
3.733
4.073
16
1.337
1.746
2.120
2.583
2.921
3.686
4.015
17
1.333
1.740
2.110
2.567
2.898
3.646
3.965
18
1.330
1.734
2.101
2.552
2.878
3.610
3.922
19
1.328
1.729
2.093
2.539
2.861
3.579
3.883
20
1.325
1.725
2.086
2.528
2.845
3.552
3.850
21
1.323
1.721
2.080
2.518
2.831
3.527
3.819
22
1.321
1.717
2.074
2.508
2.819
3.505
3.792
23
1.319
1.714
2.069
2.500
2.807
3.485
3.768
24
1.318
1.711
2.064
2.492
2.797
3.467
3.745
25
1.316
1.708
2.060
2.485
2.787
3.450
3.725
26
1.315
1.706
2.056
2.479
2.779
3.435
3.707
27
1.314
1.703
2.052
2.473
2.771
3.421
3.689
28
1.313
1.701
2.048
2.467
2.763
3.408
3.674
29
1.311
1.699
2.045
2.462
2.756
3.396
3.660
30
1.310
1.697
2.042
2.457
2.750
3.385
3.646
31
1.309
1.696
2.040
2.453
2.744
3.375
3.633
32
1.309
1.694
2.037
2.449
2.738
3.365
3.622
33
1.308
1.692
2.035
2.445
2.733
3.356
3.611
34
1.307
1.691
2.032
2.441
2.728
3.348
3.601
35
1.306
1.690
2.030
2.438
2.724
3.340
3.591
36
1.306
1.688
2.028
2.434
2.719
3.333
3.582
37
1.305
1.687
2.026
2.431
2.715
3.326
3.574
38
1.304
1.686
2.024
2.429
2.712
3.319
3.566
39
1.304
1.685
2.023
2.426
2.708
3.313
3.558
40
1.303
1.684
2.021
2.423
2.704
3.307
3.551
60
1.296
1.671
2.000
2.390
2.660
3.232
3.460
120
1.289
1.658
1.980
2.358
2.617
3.160
3.373
inf
1.282
1.645
1.960
2.327
2.576
3.091
3.291
DISTRIBUCIÓN F: Usada en teoría de probabilidad y estadística, la distribución
F es una distribución de probabilidad continua. También se le conoce como
distribución F de Snedecor (por George Snedecor) o como distribución F de
Fisher-Snedecor. Una variable aleatoria de distribución F se construye como el
siguiente cociente:
donde, U1 y U2 siguen una distribución chicuadrado con d1 y d2 grados de libertad respectivamente, y U1 y U2 son
estadísticamente independientes.
La distribución F aparece frecuentemente como la distribución nula de una prueba
estadística, especialmente en el análisis de varianza. Véase el test F. La función de
densidad de una F(d1, d2) viene dada por
para todo número real x ≥ 0, donde d1 y d2 son enteros positivos, y B es la función
beta.
DISTRIBUCIÓN JI CUADRADO: La distribución 2 (de Pearson), llamada Chi
cuadrado o Ji cuadrado, es una distribución de probabilidad continua con un
parámetro k que representa los grados de libertad de la variable aleatoria
donde Zi son variables aleatorias normales independientes de
media cero y varianza uno. El que la variable aleatoria X tenga esta distribución se
2
representa habitualmente así: X k . Es conveniente tener en cuenta que la
letra griega χ se transcribe al latín como chi y se pronuncia en castellano como ji.
Función de densidad
donde Γ es la función gamma.
DISTRIBUCIÓN EXPONENCIAL: La variable aleatoria continua X tiene una
distribución exponencial, con parámetro ß. Se dice que una variable aleatoria
continua X, tiene una distribución exponencial de parámetro β, si su función de
densidad de probabilidad es:
x
1
f ( x) e ,....x 0..... y..donde.... 0
La distribución exponencial es un caso particular de distribución gamma con k = 1.
Además la suma de variables aleatorias que siguen una misma distribución
exponencial es una variable aleatoria expresable en términos de la distribución
gamma.
DISTRIBUCIÓN UNIFORME (CONTINUA): En teoría de probabilidad y
estadística, la distribución uniforme continua es una familia de distribuciones de
probabilidad para variables aleatorias continuas, tales que cada miembro de la
familia, todos los intervalos de igual longitud en la distribución en su rango son
igualmente probables. El dominio está definido por dos parámetros, a y b, que son
sus valores mínimo y máximo. La distribución es a menudo escrita en forma
abreviada como U(a,b). La función de densidad de probabilidad de la distribución
uniforme continua es:
La función de distribución de probabilidad es:
BIBLIOGRAFÍA
Babbie, E. (2000): Fundamentos de la Investigación Social. International Thomson
Editores. México.
Benavente
del Prado, Arturo Núñez (1992): Estadística Básica par
Planificación. Editorial Interamericana. 6ª. Edición. México.
Berenso, Mark.(1.992): Estadística Básica en Administración. Editorial. Harla.
Cuarta Edición. México.
Best,J. W. (1987): Como Investigar en Educación. Editorial Morata. Madrid –
España.
Budnick Frank S. (1992): Matemáticas Aplicadas para Administración, Economía y
Ciencias Sociales. Tercera Edición. Editorial McGaw-Hill Interamericana de
México, S.A de C.V. México.
Caballero, Wilfredo (1975): Introducción a la Estadística. Editorial ICA. Costa Rica.
Cadoche, L. S.; G. Stegmayer, J. P. Burioni y M. De Bernardez (1998). Material del
Seminario de Encuestas en Educación, impartido vía internet por parte de la
Universidad Nacional del Litoral, en Santa Fe, y de la Universidad
Tecnológica Nacional, Regional Santa Fe, en la República de Argentina.
Castañeda J., J.(1991): Métodos de Investigación 2. Editorial McGraw-Hill. México.
Carono, R., Minujin, A. y Vera, G.(1982): Manual de técnicas de evaluación y
ajuste de información Estadísticas.
Fondo de cultura económica.
México.
Chao, L.(1993): Estadística para la Ciencia Administrativa. Editorial McGraw –
Hill. 4ta Edición. Colombia
Chou, Ya-Lun (1972): Análisis Estadístico. Editorial Interamericana. México
Daniel Wayne, W. y Otros (1993): Estadística con Aplicación a las Ciencias
Sociales y a la Educación. Editorial McGraw-Hill Interamericana de México,
S.A. de C.V. México.
De Oteyza de O., E; Emma Lam O., Carlos Hernández G. y Ángel M. Carrillo H.
(1998). Temas Selectos de Matemáticas. Prentice Hall. México
Enciclopedia Microsoft Encarta 2002 (2002): Censo- Cuestionario- Encuesta.
Estadística. Editorial Microsoft corporation. USA.
Erkin Kreyszia (1978): Introducción a la Estadística Matemática. Editorial Limusa,
S.A. México.
Ferrán Aranaz, Magdalena (2002) Curso de SPSS para Windows: Análisis
Estadístico. Editorial McGraw-Hill. Madrid.
Ferrán Aranaz, Magdalena (2001) SPSS para Windows: Análisis Estadístico.
Editorial McGraw-Hill. Madrid.
Filgueira, Ester (2001). Análisis de datos con SPSS Win. Alianza Editorial. Madrid.
Freud J: E. y Otros (1990): Estadística para la Administración con Enfoque
Moderno. Editorial, S.A. México.
Gomes Rondón, Francisco (1985): Estadística Metodológica: Ediciones Fragor.
Caracas.
González, Nijad H. (1986): Métodos estadísticos en Educación. Editorial Bourgeón,
Caracas.
Guilford, J. Y Fruchter, B. (1984): Estadística aplicada a la Psicología y la
Educación. Editorial McGraw-Hill Latinoamericana, S. A., Bogotá.
Hamdan González, Nijad (1986): Métodos Estadísticos en Educación. Editorial
Bourgeón C.A. Caracas – Venezuela.
Kevin, Richard I. (1988): Estadística para Administradores. Editorial
Hispanoamericana. México.
Larson Harold, J. (1985): Introducción a la Teoría de Probabilidades e inferencia
Estadística. Editorial Limusa. México.
Lehmann, Charles H. (1995): ÁLGEBRA. Editorial limusa, S.A. DE C.V. Grupo
Noriega Editores. México.
Leithold, Louis (1992): El Cálculo con Geometría Analítica. Editorial HARLA
México.
Lincon L., CHAO (1996): Estadística para Ciencias Administrativas. Cuarta edición.
Editorial McGaw-Hill. Usa.
Lenin, R.y Kubin, D.(1992): Estadística para Administradores. Editorial
Hispanoamérica. VI edición. México.
Lopez Casuso, R. (1984): Introducción al Cálculo de Probabilidades e Inferencia
Estadística. Editorial Instituto de Investigaciones Económicas, UCAB.
Caracas- Venezuela.
Mason, Robert (1.992): Estadística para la Administración y Economía.
Ediciones Alfaomega S.A.N. México.
Mendennaf, W. y OTROS (1981): Estadística para Administradores y Economía.
Editorial Iberoamericana. México.
Mode, Elmer B. (1988): Elementos de Probabilidades y Estadística Editorial
Reverte Mejicana.México.
Murria, R.(1993): Estadística. Edición Interamericana. 2da Edición. México.
Pardo Merino, Antonio y Ruiz Díaz, Miguel Ángel (2002). SPSS 11. Guía para
Análisis de Datos. Editorial McGraw-Hill. Madrid.
Pardo Merino, Antonio y Ruiz Díaz, Miguel Ángel (2005). Análisis de datos con
SPSS 13 Base. Editorial McGraw-Hill. Madrid.
Parzen, E. (1986): Teoría Moderna de Probabilidades y sus Aplicaciones Editorial
Limusa. México
Peña, Daniel y Romo, Juan (1999). Introducción a la estadística para las Ciencias
Sociales. Editorial McGraw-Hill. Madrid.
Pérez López, César. 2002. Estadística aplicada a través de Excel. Editorial Pearson
Prentice Hall. Madrid.
Pérez López, C. (2005): Técnicas Estadísticas con SPSS 12. Editorial Pearson
Prentice Hall. Madrid.
Pérez López, C. (2004): Técnicas de Análisis Multivariante de Datos: Aplicaciones
con SPSS . Editorial Pearson Prentice Hall. Madrid.
Pérez López, C. (2001). Técnicas estadísticas con SPSS. Editorial Pearson Prentice
Hall. Madrid.
Pérez López, C. (2005): Métodos Estadísticos Avanzados con SPSS. Internacional
Thomson Editores Spain. Madrid.
Pugachev, V. S. (1973): Introducción a la Teoría de Probabilidades Editorial Mir.
Moscú.
Rivas González, Ernesto(1980): Estadística General. Ediciones de la Biblioteca
UCV. Caracas – Venezuela.
Ritchey, F.J. (2002): Estadística para las Ciencias Sociales. Ed. McGraw – Hill.
México.
Sánchez Carrión, Juan Javier (2004). Manual de análisis estadístico de los datos.
Alianza Editorial. Madrid.
Soto Negrin, Armando (1982): Iniciación a la estadística. Editorial José Marti.
Caracas - Venezuela.
Spiegel, M.R. y Stephens Larry j. (2002): Estadística. Mc Graw Hill Interamericana
de España. S.A. Madrid.
Stephen P., Shao (1986): Estadística para Economistas y Administradores de
Empresa.Editorial Herreros Hermanos, Sucs., S.A., México.
Stevenson, William (1991): Estadística para la Administración y Económica.
Editorial Harla. México.
Visauta Vinacua, Bienvenido (2002) Análisis estadístico con SPSS para Windows
Volumen I: Estadística Básica. Editorial McGraw – Hill INTERAMERICANA DE
ESPAÑA, S.A.U. México.
Visauta Vinacua, Bienvenido (2005) Análisis estadístico con SPSS para Windows
Volumen
II:
Estadística
Multivariante.
Editorial
McGraw
–
Hill
INTERAMERICANA DE ESPAÑA, S.A.U. México.
Universidad Nacional Experimental “Simón Rodríguez” (1983): Estadística 1.
Ediciones UNESR, Caracas.
Walpole, R. y Myers, R. (1987): Probabilidad y Estadística para Ingenieros.
Editorial Interamericana. México.
Webster, Allen L (2001) Estadística Aplicada a los Negocios y la Economía.
Editorial McGraw – Hill INTERAMERICANA DE BOGOTA, S.A.U. Colombia.
Weimer, Richard C. (1996) Estadística. Compañía Editorial Continental, SA deCV.
México.
Wonnacott, T. H. y Wonnacott, R: J. (1989): Fundamentos de Estadística para
Administración y Economía. Editorial LIMUSA. México.
BIBLIOWEB
https://sites.google.com/site/educacionvirtualdelsigloxxi/
https://sites.google.com/site/aprendizajedeestadistica /
https://sites.google.com/site/estadisticaconelspss /
http://hamletyelaprendizajevirtual.jimdo.com /
http://aprendizajevirtuylastic.wordpress.com /
http://hamletylaestadisticaugma.jimdo.com /
http://aprendizajevirtuaylastic.jimdo.com /
https://sites.google.com/site/hamletylastic /
http://hamletyestadisticaspss.jimdo.com /
http://www.udemy.com/draft/12005
http://rossyindriagosilva.jimdo.com /
http://equposanantonio.jimdo.com /
http://hamletmud.jimdo.com /
http://postgradougma.jimdo.com
http://www.bioestadistica.uma.es/libro/
http://www.hrc.es/bioest/Mdocente.html#tema1
http://www.mailxmail.com/curso/informatica/spssespanol/capitulo1.htm (SPSS)
http://www.aulafacil.com/investigacionspss/Lecc-6.htm (SPSS)
http://home.ubalt.edu/ntsbarsh/Business-stat/opre504S.htm
http://nutriserver.com/Cursos/Bioestadistica/Distribuciones_Continuas.html
http://www.bioestadistica.freeservers.com/farpro.html
http://www.gestiopolis.com/canales/financiera/articulos/36/estapro.htm
http://www.hrc.es/bioest/Reglin_8.html
http://www.monografias.com/trabajos20/estadistica/estadistica.shtml
http://nutriserver.com/Cursos/Bioestadistica/Distribuciones_Bidimensionales.html
http://www.terra.es/personal2/jpb00000/tvariablealeatoria.htm
http://www.terra.es/personal2/jpb00000/tinferencia.htm#muestreoaleatoriosimpl
e
http://es.wikipedia.org/wiki/Distribuci%C3%B3n_de_probabilidad
http://w3.mor.itesm.mx/~cmendoza/ma835/ma83500.html
http://www.seh-lelha.org/noparame.htm
http://sapiens.ya.com/matagus/unidad6.htm
http://zip.rincondelvago.com/?00044092
http://www.seh-lelha.org/regresion1.htm
http://www.eumed.net/cursecon/medir/introd.htm
http://encyclopedie-es.snyke.com/articles/distribucion_de_probabilidad.html
http://www.seh-lelha.org/concor2.htm
http://www.seh-lelha.org/noparame.htm
http://www.inf.ufsc.br/cee/pasta1/art4.html
http://www.inf.ufsc.br/cee/pasta4/art1p4.html
http://buscar.hispavista.com/?cadena=Aprende+estadistica
http://www.psicol.unam.mx/Cim2000/Estadistica/journal_of_statistics_education.
htm
http://www.statserv.com/softwares.html
http://www.statistics.com/
http://e-stadistica.bio.ucm.es/web_spss/entorno_de_trabajo_del_SPSS.html
http://www.hrc.es/bioest/Introducion_ch.html
http://www.hrc.es/bioest/M_docente.html#tema2
http://members.tripod.com/~beatrizt/verdad/5.html
http://www.monografias.com/trabajos5/estadm/estadm.shtml
http://www.monografias.com/trabajos10/esta/esta.shtml
http://platea.pntic.mec.es/~jescuder/estadist.htm
http://www.angelfire.com/journal2/estadistica/Links.htm
http://www.edustatspr.com/documentos/probabilidad/3.1.vadiscr.pdf
http://www.fisterra.com/material/investiga/distr_normal/distr_normal.htm
http://www.caib.es/ibae/esdeveniment/jornades_10_01/doc/Estepa-JornadasMallorca.doc