CURSO DE METODOS CUANTITATIVOS ACTIVIDADES A DESARROLLAR ACTIVIDAD No. 4

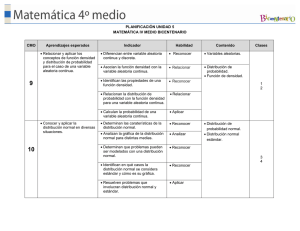
CURSO DE METODOS CUANTITATIVOS
ACTIVIDADES A DESARROLLAR
ACTIVIDAD No. 4
DISTRIBUCIONES DE PROBABILIDAD DISCRETA
a) Distribución de probabilidad.
Relación de los posibles resultados de un experimento y la probabilidad asociada con
cada resultado.
b) Características de una distribución de probabilidad.
Proporciona toda la variedad de valores que se pueden presentar en un experimento,
es similar a una distribución de frecuencias relativas. Sin embargo, en lugar de describir
el pasado, esta describe la posibilidad de que se presente un evento futuro.
c) Variable aleatoria.
Valor que se obtiene de un experimentó que puede, por casualidad, resultar en
diferentes valores.
Resultado que se obtiene al azar en un experimento y que puede asumir valores
diferentes.
d) Variable aleatoria discreta.
Variable aleatoria que puede suponer sólo ciertos valores independientes.
e) Variable aleatoria continua.
Variable aleatoria que puede suponer un numero infinito de valores dentro de un rango
dado.
f) Distribución de probabilidad discreta.
Si se organiza un conjunto de valores posibles de una variable aleatoria discreta en una
distribución de probabilidad, lo que se obtiene es Distribución de probabilidad discreta
g) Cálculo de la media, varianza y desviación estándar de una distribución de
probabilidad.
Media: es un valor típico que se utiliza para representar la ubicación central de una
distribución de probabilidad; también es el valor promedio prevaleciente de la variable
aleatoria. También se describe como su valor esperado.
Varianza: Mide el grado de dispersión de la distribución de probabilidades
Desviación estándar: Es la raíz cuadrada del varianza
h) Distribución de probabilidad binomial.
Se divide en 4 pasos:
1.- Los resultados de cada prueba de un experimento se clasifican en una de dos
categorías exclusivas, un éxito o un fracaso.
2.- La variable aleatoria cuenta el numero de éxitos en un numero fijo de pruebas o
ensayos
3.- La probabilidad de éxitos y fracasos permanece igual en todas las pruebas o
ensayos.
4.- Las pruebas son independientes, lo que significa que el resultado de una prueba o
ensayo no afecta el resultado de cualquier otra.
i) Construcción de una distribución de probabilidad binomial.
Para crearla utilizamos
1.- El numero de ensayos
2.- la probabilidad de éxitos en cada ensayo.
j) Tablas de probabilidad binomial.
Una distribución de probabilidad binomial es una distribución teórica, que se puede
calcular mediante el uso de una fórmula. Sin embargo, los cálculos pueden ser muy
tediosos. Por tal motivo existen tablas en las que se pueden consultar las
probabilidades de un determinado número de éxitos para varios valores de n y de p.
k) Media de una distribución binomial.
l)
Varianza de una distribución binomial.
m) Distribuciones de probabilidad acumulada.
La función de distribución acumulada es llamada también Distribución de Probabilidad
Acumulada, y se consiste en una lista de los posibles resultados de un experimento
asociados a la probabilidad de que ocurra cada uno de ellos más la probabilidad de que
ocurran los anteriores.
n) Distribución de probabilidad hipergeométrica.
Se basa en una variable aleatoria discreta. Sus características mas importantes son:
1.- los resultados en cada prueba de un experimento se clasifican en una de dos
categorías exclusivas: un éxito o un fracaso.
2.- La variable aleatoria es el numero de éxitos en un numero fijo de pruebas
3.- Las pruebas no son independientes.
4.- se supone que los muestreos se realizan con una población finita sin reemplazos.
Por tanto, la probabilidad de un éxito cambia en cada prueba.
o) Distribución de probabilidad de poisson.
Describe el numero de veces que ocurre un evento durante un intervalo especifico. El
intervalo puede ser tiempo, distancia, área o volumen.
Se utiliza con frecuencia para aproximar probabilidades binominales cuando n es grande
y π es pequeño. Que se entiende por grande y pequeño no esta definido con precisión,
pero una norma general es que n debe de ser igual a o mayor que 20 y π debe de ser
igual a o menor que 0.05