Teor´ıa clásica de la optimización
Anuncio

Teorı́a clásica de la optimización
En la teona clásica de la optimización se usa el cálculo diferencial para determinar puntos extremos, o de máximo o mı́nimo, para funciones sin restricciones
y restringidas. Puede ser que los métodos no sean adecuados para cálculos
numéricos eficientes, pero la teorı́a básica proporciona el fundamento de la
mayor parte de los algoritmos de programación no lineal. Ahora estableceremos las condiciones necesarias y suficientes para determinar puntos extremos
no restringidos, los métodos (del) jacobiano y (del) lagrangiano para problemas
con restricciones de igualdad, y las condiciones de Karush-Kuhn-Tucker para
problemas con restricciones de desigualdad.
Problemas sin Restricción
Un punto extremo de una función f (X) (campo escalar) define un máximo o
un mı́nimo de ella. Matemáticamente, un punto X0 = (x01 , . . . , x0j , . . . , x0n ) es
máximo si
f (X0 + h) ≤ f (X0 )
para toda h = (h01 , . . . , h0j , . . . , h0n ) y |hj | es suficientemente pequeña para toda
j. En otras palabras, X0 es un valor máximo si el valor de f en cada punto
de la proximidad de X0 no es mayor que f (X0 ). En forma parecida, X0 es un
mı́nimo si
f (X0 + h) ≥ f (X0 )
La figura 1 ilustra los máximos y mı́nimos de una función f (x) de una sola
variable dentro del intervalo [ a, b ]. Los puntos x1 , x2 , x3 , x4 y x6 son extremos
de f (x), x1 , x3 y x6 son máximos, x2 y x4 son mı́nimos. Ya que
f (x6 ) = máx{f (x1 ), f (x3 ), f (x6 )}
f (x6 ) es un máximo global o absoluto, f (x1 ) y f (x3 ) son máximos locales
o relativos. De igual modo, f (x4 ) es un mı́nimo local y f (x2 ) es un mı́nimo
global.
Aunque x1 (en la figura 1) es un punto máximo, se diferencia de los otros
máximos locales porque el valor de f correspondiente a al menos un punto en
la proximidad de x1 es igual f (x1 ). A este respecto, es un máximo débil,
mientras que x3 y x4 son máximos fuertes. En general, X0 es un máximo
débil si f (X0 +h) ≤ f (X0 ), y es un máximo fuerte si f (X0 +h) < f (X0 ), donde
h es como se definió arriba.
En la figura 1, la primera derivada o pendiente de f es igual a cero en todos los
puntos extremos. Esta propiedad también se satisface en puntos de inflexión y
de silla, como x5 . Si un punto con pendiente (gradiente) cero no es un extremo
(máximo o mı́nimo), debe ser un punto de inflexión o un punto de silla.
1
Figure 1: Ejemplos de puntos extremos para una función de una variable
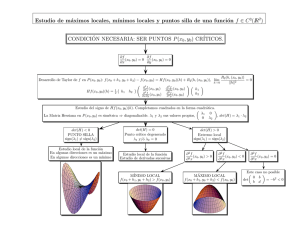
Condiciones necesarias y suficientes
En esta sección se presentan las condiciones necesarias y suficientes para que
una función f (X) de n variables tenga puntos extremos. Se supone que las
derivadas primera y segunda de f (X) son continuas en toda x.
Teorema 1: Una condición necesaria para que X0 sea un punto extremo de
f (X) es que
∇f (X0 ) = 0
Demostración: De acuerdo con el teorema de Taylor, para 0 < θ < 1,
1
f (X0 + h) − f (X0 ) = ∇f (X0 )h + hT Hh|X0 +θh
2
en donde h es lo que se definió antes. Para |hj | suficientemente pequeña, el
término restante 21 hT Hh es del orden de h2j , y entonces
f (X0 + h) − f (X0 ) = ∇f (X0 )h + O(h2j ) ≈ ∇f (X0 )h
Se puede demostrar, por contradicción, que ∇f (X0 ) debe anularse en un punto
mı́nimo X0 . Si no lo hiciera, para una j especı́fica, la condición siguiente será
válida:
∂f (X0 )
∂f (X0 )
<0 o
>0
∂xj
∂xj
Si se selecciona hj con el signo adecuado, siempre es posible tener
hj
∂f (X0 )
<0
∂xj
2
Igualando a cero las demás hj , con el desarrollo de Taylor se obtiene
f (X0 + h) < f (X0 )
Este resultado contradice la hipótesis que X0 es un punto mı́nimo. En consecuencia ∇f (X0 ) debe ser igual a cero. Se puede hacer una demostración similar
para el caso de la maximización.
Como la condición necesaria también queda satisfecha con los puntos de inflexión
y de silla, los puntos obtenidos con la solución de
∇f (X0 ) = 0
se llaman puntos estacionarios. El teorema que sigue establece las condiciones
para que X0 sea un punto extremo.
Teorema 2: Una condición suficiente para que un punto estacionario X0 sea
un punto extremo es que la matriz hessiana H evaluada en X0 satisfaga las
siguientes condiciones:
1. Que H sea positiva definida si X0 es un punto mı́nimo.
2. Que H sea negativa definida si X0 es un punto máximo.
Demostración. De acuerdo con el teorema de Taylor, para 0 < θ < 1,
1
f (X0 + h) − f (X0 ) = ∇f (X0 )h + hT Hh|X0 +θh
2
Ya que X0 es un punto estacionario, entonces ∇f (X0 ) = 0 (Teorema 1). Ası́,
f (X0 + h) − f (X0 ) =
1 T
h Hh|X0 +θh
2
Si X0 es un punto mı́nimo, entonces
f (X0 + h) > f (X0 ), h 6= 0
Entonces, para que X0 sea un punto mı́nimo, se debe cumplir
1 T
h Hh|X0 +θh > 0
2
Ya que la segunda derivada parcial es continua, la expresión 12 hT Hh debe tener
el mismo signo tanto en X0 como en X0 + θh. Como 12 hT Hh|X0 define a una
forma cuadrática, esta expresión (y en consecuencia 12 hT Hh|X0 +θh ) es positiva si, y sólo si H|X0 es positiva definida. Eso quiere decir que una condición
suficiente para que el punto estacionario X0 sea un mı́nimo es que la matriz hessiana H, evaluada en el mismo punto, sea positiva definida. Una demostración
3
similar para el caso de la maximización indica que la matriz hessiana correspondiente debe ser negativa definida.
Ejemplo 20.1-1
Se tiene la función
f (x1 , x2 , x3 ) = x1 + 2x3 + x2 x3 − x21 − x22 − x23
La condición necesaria
∇f (X0 ) = 0
da como resultado
∂f
∂x1
∂f
∂x2
∂f
∂x3
=
1 − 2x1 = 0
= x3 − 2x2 = 0
=
2 + x2 − 2x3 = 0
La solución de estas ecuaciones simultáneas es
X0 = (1/2, 2/3, 4/3)
Para establecer la suficiencia se examina
∂2f
∂2f
∂2f
H|X0
=
∂x21
∂2f
∂x2 ∂x1
∂2f
∂x3 ∂x1
∂x1 ∂x2
∂2f
∂x22
∂2f
∂x3 ∂x2
∂x1 ∂x3
∂2f
∂x2 ∂x3
∂2f
∂x23
−2
0
0
1
= 0 −2
0
1 −2
X0
Los determinantes menores principales de H|X0 tienen los valores −2, 4 y −6,
respectivamente. Ası́, H|X0 es negativa definida y X0 = (1/2, 2/3, 4/3) representa un punto máximo.
En general, si H|X0 es indefinida, X0 debe ser un punto de silla. Para casos
inciertos, X0 puede ser o no un punto extremo, y la condición de suficiencia se
vuelve muy complicada, porque se deben considerar términos de orden superior
en el desarrollo de Taylor.
La condición de suficiencia establecida por el teorema 2 se aplica a funciones
de una variable como se verá a continuación. Si y0 es un punto estacionario,
entonces
1. y0 es un máximo si f 0 (y0 ) < 0.
2. y0 es un mı́nimo si f 0 (y0 ) > 0.
4
Figure 2: Puntos extremos de f (y) = y 4 y g(y) = y 4 .
Si en caso de una variable f 00 (y0 ) = 0, se deben investigar derivadas de orden
superior, como indica el siguiente teorema.
Teorema 3: Dado y0 , un punto estacionario de f (y), si las primeras (n − 1)
derivadas son cero y si f (n) (y0 ) 6= 0, entonces
1. y0 es un punto de inflexión si n es impar.
2. y0 es un punto mı́nimo si n es par y f (n) (y0 ) > 0.
3. y0 es un punto máximo si n es par y f (n) (y0 ) < 0.
Ejemplo 20.1-2
En la figura 2 se ven las gráficas de las dos funciones siguientes:
f (y) = y 4 ,
g(y) = y 3
con la que se obtiene el punto estacionario y0 = 0. Ahora bien,
f 0 (0) = f 00 (0) = f (3) (0) = 0, y f (4) = 24 > 0
Por consiguiente, y0 = 0 es un punto mı́nimo (véase la figura 2). Esto indica
que y0 = 0 es un punto estacionario. También
g 0 (0) = g 00 (0) = 0, g (3) = 6 6= 0
En consecuancia, y0 es un punto de inflexión.
El método de Newton-Raphson
En general, las ecuaciones de condición necesaria, ∇f (X) = 0, pueden ser
difı́ciles de resolver numéricamente. El método de Newton-Raphson es un procedimiento iterativo para resolver ecuaciones simultáneas no lineales. Aunque
5
aquı́ se presenta el método en este contexto, en realidad es parte de los métodos
de gradiente para optimizar numéricamente funciones no restringidas.
Se tienen las ecuaciones simultáneas
fi (X) = 0, i = 1, 2, . . . , m.
Sea Xk un punto dado. Entonces, con el desarrollo de Taylor,
fi (X) ≈ fi (Xk ) + ∇fi (Xk )(X − Xk ), i = 1, 2, . . . , m.
Ası́, las ecuaciones originales, fi (X) = 0, i = 1, 2, . . . , m se pueden aproximar
de esta forma:
fi (Xk ) + ∇fi (Xk )(X − Xk ) = 0, i = 1, 2, . . . , m.
Estas ecuaciones se pueden escribir con notación matricial del siguiente modo:
Ak + Bk (X − Xk ) = 0
Si Bk es no singular, entonces
X = Xk − B−1
k Ak
La idea del método es comenzar en un punto inicial X0 . Al aplicar la ecuación
anterior se determina un punto nuevo Xk+1 a partir de Xk . El procedimiento
termina en Xm como punto de solución, cuando Xm ≈ Xm−1 .
Se ilustra en la figura 3 una interpretación geométrica del método, con una
función de una sola variable. La relación entre xk y xk+1 para una función f (x)
de una variable se reduce a
xk+1 = xk −
o bien
f 0 (xk ) =
f (xk )
f 0 (xk )
f (xk )
− xk+1
xk
En la figura se ve que xk+1 se determina con la pendiente f (x) en xk , siendo
tan t = f 0 (xk ). Una dificultad del método es que no siempre se garantiza la convergencia, a menos que la función f tenga buen comportamiento. En la figura 3,
si el punto inicial es a, el método diverge. No hay manera fácil de ubicar un
“buen” punto inicial.
6
Figure 3: Ilustración del proceso iterativo del método de Newton-Raphson.
7