La+regla+de+Barrow ver1

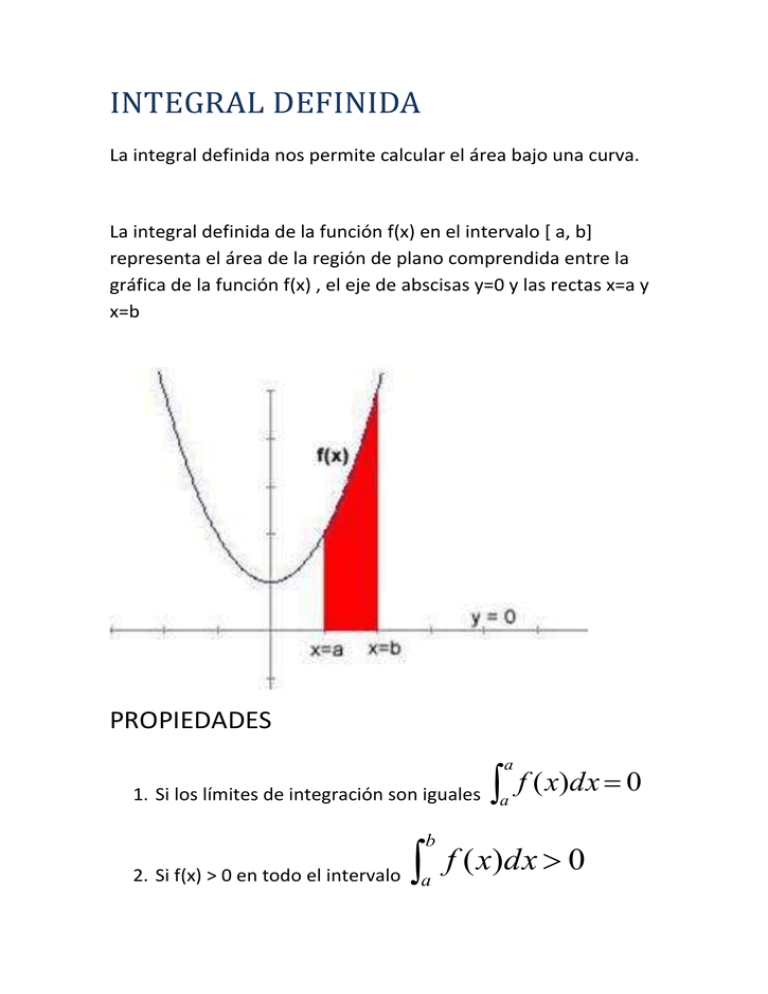
INTEGRAL DEFINIDA
La integral definida nos permite calcular el área bajo una curva.
La integral definida de la función f(x) en el intervalo [ a, b]
representa el área de la región de plano comprendida entre la
gráfica de la función f(x) , el eje de abscisas y=0 y las rectas x=a y
x=b
PROPIEDADES

a
1. Si los límites de integración son iguales a

b
2. Si f(x) > 0 en todo el intervalo a
f ( x)dx  0
f ( x)dx  0
Si f(x) <o en todo el intervalo

b
a
f ( x)dx  0
3. Si f(x) es continua en [a,b] [a,c] [c,b] y a<c<b entonces
b

a
c
b
a
c
f ( x)dx  f ( x)dx   f ( x)dx
4. Si f(x) es continua en [a,b] entonces:
b

a
a
f ( x)dx   f ( x)dx
b
5. Si f(x) y g(x) son continuas en [a,b]:
b
b
a
a
 [ f ( x)  g ( x)]dx 
b
f ( x)dx   g ( x)dx
a
6. Si f(x) es continua en [a,b] y k es una constante:
b
b
a
a
 kf ( x)dx k 
f ( x)dx
7. Si f(x)  g (x) para cualquier valor de x 
b

a
b
f ( x)dx  g ( x)dx
a
a, b
La regla de Barrow es una propiedad de las funciones continuas y que
permite calcular fácilmente el valor de la integral definida a partir de
cualquiera de las primitivas de la función.
Dada una función f(x) continua en el intervalo [a,b] y sea F(x)
cualquier función primitiva de f, es decir F '(x) = f(x). Entonces
EJERCICIOS :
1.

3
0
( x 2  4 x 
x
 3)dx 
5
3


3
2
 x

x
1x
4

 3x  

3 5 2
 3


 0
2
8
1 9
9 8
9
27  .  9   
27
3
5 2
10 3
3
2
2. Calcula el área definida por la curva y=x3 -6x2+8x y el eje 0X

2
0
=
4
(x - 6x + 8x)dx   (x3 - 6x2 + 8x )dx
3
2
2
4  4 8
3. Calcula el área comprendida entre la función
f(x) = ex , el eje de abscisas y las rectas x=1 y
x=2
2
 e dx  e
1
x
x 2
1
 e  e  ee  1
2
1
4. Una fábrica creada en 1990 ve cómo poco a
poco empieza a desgastarse su equipo, por lo
que sus costes de mantenimiento empiezan a
aumentar. Si se conoce que el incremento de
esos costes viene dado por la función M’(t) =
140 t2+9800 en euros por año (t) ¿ qué coste
tendrá esta fábrica desde el año 2000 al año
2005?
5
3


140
t
2
0 (140t  9800)dt   3  9800t  
0
5
17500
 49000 54833euros
3
5. La función de coste marginal de un
fabricante es : C’ = dC/Dq= 0,8q+4 . Si
actualmente la fábrica produce q=50 unidades
al día. ¿Cuánto costará doblar la producción?
100
C (100)  C (50)  
50
100
 0,8 2

(0,8q  4)dq   q  4q  
 2
 50
 800

 400  1000 200  3200

 2
