tema 6. Integral definida 18-19

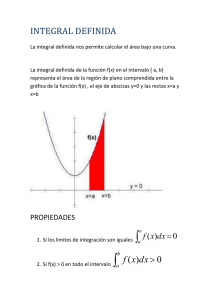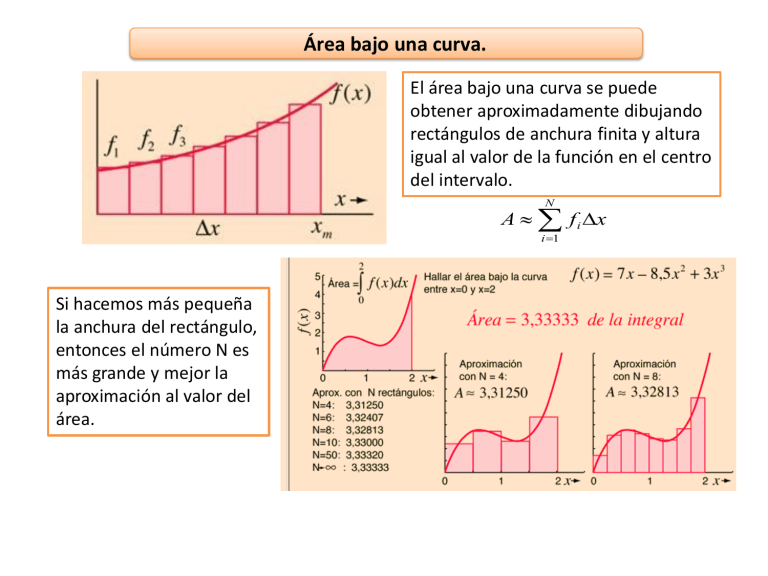
Área bajo una curva.
El área bajo una curva se puede
obtener aproximadamente dibujando
rectángulos de anchura finita y altura
igual al valor de la función en el centro
del intervalo.
N
A   f i x
i =1
Si hacemos más pequeña
la anchura del rectángulo,
entonces el número N es
más grande y mejor la
aproximación al valor del
área.
Sumas de Riemann. Integral definida.
Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre
la gráfica de f(x), el eje de abscisas, y las rectas verticales x = a y x = b.

b
a
N
f ( x) dx = lim  f i ( x) x
x →0
i =1
SUMAS DE RIEMANN.
b
La integral definida se representa por  f ( x ) dx
a
∫ es el signo de integración.
a límite inferior de la integración.
b límite superior de la integración.
f(x) es el integrando o función a integrar.
dx es diferencial de x, e indica cuál es la variable de la función que se integra.
Propiedades.
b
a

 f ( x)dx = 0
 ( f ( x) + g ( x) )dx =  f ( x)dx + 
 k· f ( x)dx = k· f ( x)dx; k  
 f ( x)dx +  f ( x)dx =  f ( x)dx
a
a
f ( x) dx = −  f ( x) dx
b
a
b
a
b
b
b
a
a
g ( x) dx
b
a
c
a
b
a
b
c
a
Otras propiedades.
b
Si f  0 en [a, b]   f ( x)dx  0
a
b
b
a
a
Si f  g en [a, b]   f ( x)dx   g ( x)dx
b
Si m  f  M en [a, b]  m(b − a )   f ( x)dx  M (b − a )
a

b
a
f ( x ) dx 

b
a
f ( x ) dx
Teorema del valor medio del cálculo integral.
Si una función es continua en unb intervalo cerrado [a, b], existe un punto c en el
interior del intervalo tal que: a f ( x) dx = (b − a )· f (c)
DEM.
b
Si una función es continua en un intervalo cerrado [a, b],  f ( x ) dx

a
y siendo m y M el mínimo y el máximo de f en [a, b],
b
Si m  f  M en [a, b]  m(b − a )   f ( x)dx  M (b − a )
a
1 b
f ( x)dx  M
b − a a
1 b
Luego b − a a f ( x)dx está comprendido entre el
máximo y el mínimo de f en [a,b],
m
Al númerof (c) se le llama valor
medio de f en el intervalo [a,b]
Y aplicando el teorema de Bolzano de los valores
intermedios,
1
c  [ a, b] / f (c) =
b−a
 f (c)·(b − a ) =
Tema 6. Integral definida.


b
a
b
a
f ( x) dx
f ( x) dx
Teorema del valor medio del cálculo integral.
Halla el valor medio de f.
El valor buscado, se obtiene a partir del área de la figura limitada por f, el eje X, y las
rectas x=0 y x=2 (un trapecio de bases 1 y 2 y altura 1, y un cuarto de círculo de
radio 1).

2
0
2 +1
 ·12 6 + 
f ( x) dx = f (c)·2 =
·1 +
=
2
4
4
 f (c ) =
6+
8
La regla de Barrow.
La regla de Barrow dice que la integral definida de una función continua f(x) en un intervalo
cerrado [a, b] es igual a la diferencia entre los valores que toma una función primitiva G(x)
de f(x), en los extremos de dicho intervalo.

b
a
f ( x) dx = F (b) − F ( a )
DEM.
Dividimos el intervalo [a,b] en n subintervalos iguales con los puntos a = x0  x1  ...  xn = b
Si F es una primitiva de f, se puede calcular,
n
F (b) − F (a) = F ( xn ) − F ( xn −1 ) + F ( xn −1 ) + ... + F ( x2 ) − F ( x1 ) + F ( x1 ) − F ( x0 ) =  (F ( xi ) − F ( xi −1 ) )
i =1
Como F es continua, pues es derivable por ser primitiva
n de f, aplicando el teorema del
Valor medio en cada intervalo tenemos F (b) − F (a) =  F ' (ci )(xi − xi −1 ), ci  ( xi −1 , xi )
i =1
n
Tomando límites lim  f (ci )x = lim (F (b) − F (a) )
n → +

i =1
b
a
n → +
f ( x ) dx = F (b) − F ( a )
x
Teorema fundamental del Cálculo.
Si f es continua en [a,b] y F está definida en [a,b] por
[a,b] y F’=f(x).

x
a
f (t ) dt , entonces F es derivable en
DEM.
Usamos las propiedades de integral definida y definición de derivada.
x
F ( x + h) − F ( x ) 1  x + h
1
= 
f (t ) dt −  f (t ) dt  =
a
 h
h
h a

x+h
x
f (t ) dt
Como f es continua en [a,b], también lo es en [x,x+h] y por el teorema del valor medio del
Cálculo integral

x+h
x
f (t ) dt = f (c)·( x + h − x) = f (c)·h, c  [ x, x + h]
F ( x + h) − F ( x ) 1
= · f (c)·h = f (c), c  [ x, x + h]
h
h
f (c ) =
Como f es continua en [x,x+h], si h → 0, c  [ x, x + h]  lim
h →0
Así pues,
F ' ( x) = lim
h →0
F ( x + h) − F ( x )
= lim f (c) = f ( x)
h →0
h
f ( x)
Áreas de recintos planos.
Pueden ocurrir varios casos:
1. Región limitada por la gráfica de una función continua no negativa en [a,b],
el eje horizontal y las rectas verticales x=a y x=b:

b
a
f ( x) dx = F (b) − F ( a )
Por ejemplo.
Calcular el área limitada por la curva xy = 36, el eje OX y las rectas: x = 6, x = 12.
12
A=
6
36
12
dx = 36 ln x 6 = 36 ln 2u 2
x
Áreas de recintos planos.
2. Región limitada por una función no negativa continua en [a,b] y el eje horizontal:
Para hallar el área seguiremos los siguientes pasos:
1º Se calculan los puntos de corte con el eje OX, haciendo f(x) = 0 y resolviendo la ecuación.
2º El área es igual a la integral definida de la función con límites de integración los puntos de corte.

b
a
f ( x ) dx = F (b) − F ( a )
Por ejemplo.
Calcular el área del recinto limitado por la curva y = 9 − x2 y el eje OX.
En primer lugar hallamos los puntos de corte con el eje OX para representar la curva y
conocer los límites de integración.
0 = 9 − x 2 ; x = 3 ; x = −3
Como la parábola es simétrica respecto al eje OY, el área será
igual al doble del área comprendida entre x = 0 y x = 3.
3
(
)
A =  9 − x 2 dx = 2
−3
3
0
3

x3 
2
9 − x dx = 29 x −  = 36u 2
3 0

(
)
Áreas de recintos planos.
3. Región limitada por una función continua en [a,b], el eje horizontal y las rectas
verticales x=a y x=b:
En ese caso el recinto tiene zonas por encima y por debajo del eje de abscisas. Para calcular el
área de la función seguiremos los siguientes pasos:
1º Se calculan los puntos de corte con el eje OX, haciendo f(x) = 0 y resolviendo la ecuación.
2º Se ordenan de menor a mayor las raíces, que serán los límites de integración.
3º El área es igual a la suma de las integrales definidas en valor absoluto de cada intervalo.
Por ejemplo.
Hallar el área limitada por la recta
, el eje de abscisas y las ordenadas
correspondientes a x = 0 y x = 4.
1 3 2
1
 3x − 6 

2
(
)
A1 =  
dx
=
x
−
6
x
=
6
−
12
=
−
3
u


0
2  2
2
 2 
0
4
4  3x − 6 
1 3 2
1

2
(
)
(
)


A2 =  
dx
x
6
x
=
24
−
24
−
6
−
12
=
3
u
=
−


2
2  2
2
 2 
2
2
2
A = A1 + A2 = − 3 + 3 = 6u 2
Áreas de recintos planos.
4. Región limitada por dos funciones continua en [a,b]:
El área comprendida entre dos funciones es igual al área de la función que está
situada por encima menos el área de la función que está situada por debajo
 g ( x) −
b
a
f ( x)dx
Por ejemplo.
Calcular el área del recinto limitado por la parábola y = x2 + 2 y la recta que pasa por los
puntos (−1, 0) y (1, 4).
x +1 y
= → 4( x + 1) = 2 y → y = 2 x + 2
1+1 4
 y = x2 + 2
→ x1 = 0, x2 = 2

 y = 2x + 2
0
2
 2 x3 
8 4
2
2 x + 2 − x − 2 dx =  x −  = 4 − = u 2
3 0
3 3

(
2
)
¿Si lo hacemos al revés? El área sería negativa y
no es posible. Debería ser al contrario.
Volumen de sólidos de revolución.
b
V =   ( f ( x)) 2 dx
a
Sólo por dar una idea, diremos que dicha fórmula se obtiene considerando que el radio en cada
corte circular es el valor de
. El procedimiento de cálculo integral, utiliza
límites de sumas de volúmenes de pequeñas arandelas o cortes circulares infinitesimales del
sólido de revolución.
Volumen de sólidos de revolución.
Por ejemplo.
Hallar el volumen engendrado por el círculo x2 + y2 − 4x = −3 al girar alrededor del eje OX.
x 2 − 4 x + 4 − 4 + y 2 = −3
(x − 2)2 + y 2 = 1
El centro de la circunferencia es C(2,0) y el radio r = 1.
Puntos de corte con el eje OX:
( x − 2 )2 + y 2 = 1
→ (1,0 ); (3,0 )

y = 0
3
𝑉 = 𝜋න
1
−𝑥 2 + 4𝑥 − 3
2
3
1
𝑑𝑥 = 𝜋 න −𝑥 2 + 4𝑥 − 3 𝑑𝑥 = 𝜋 − 𝑥 3 + 2𝑥 2 − 3𝑥
3
1
3
1
4𝜋 3
= 𝑢
3
Volumen de sólidos de revolución.
Por ejemplo.
Calcular el volumen que engendra un triángulo de vértices A(3, 0), B(6, 3), C(8, 0) al girar
360° alrededor del eje OX.
Ecuación de la recta que pasa por AB:
Ecuación de la recta que pasa por BC:
x −3 y
= → 3(x − 3) = 3 y → y = x − 3
6−3 3
x −8 y
3
= → 3(x − 8) = −2 y → y = − (x − 8)
2
6−8 3
2
 3

V =   ( x − 3) dx +   − ( x − 8) dx =
3
6
 2

6
8 9

2
=   (x − 6 x + 9 )dx +    (x 2 − 16 x + 64 ) dx =
6 4
3


6
8
2
6
8
 x3
 9  x 3

2
2
=   − 3x + 9 x  +
−
8
x
+
64
x

 =
3
4
3

3

6
=  (72 − 108 + 54 − 9 + 27 − 27 ) +
9  512

− 512 + 512 − 72 + 288 − 384  = 15u 3

4  3

Longitud de arcos.

b
a
1 + ( f ' ( x)) 2 dx
Por ejemplo.
Hallar la longitud del arco de curva
en el intervalo [0, 1]
2
1
1
3
3 
9

y '=
x
L =  1 +  x  dx =  1 + x dx
0
0
2
4
2 
9
1+ x = t 2
x = 0 → t =1
4
9
8
13
dx = 2tdt → dx = tdt
x =1→ t =
4
9
2
L=
1
13
2
8
8 t 
t dt =  
9
9  3 1
3
13
2
8  13 13 
= 
− 1
27  8
