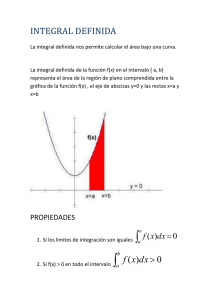
Resumen características funciones

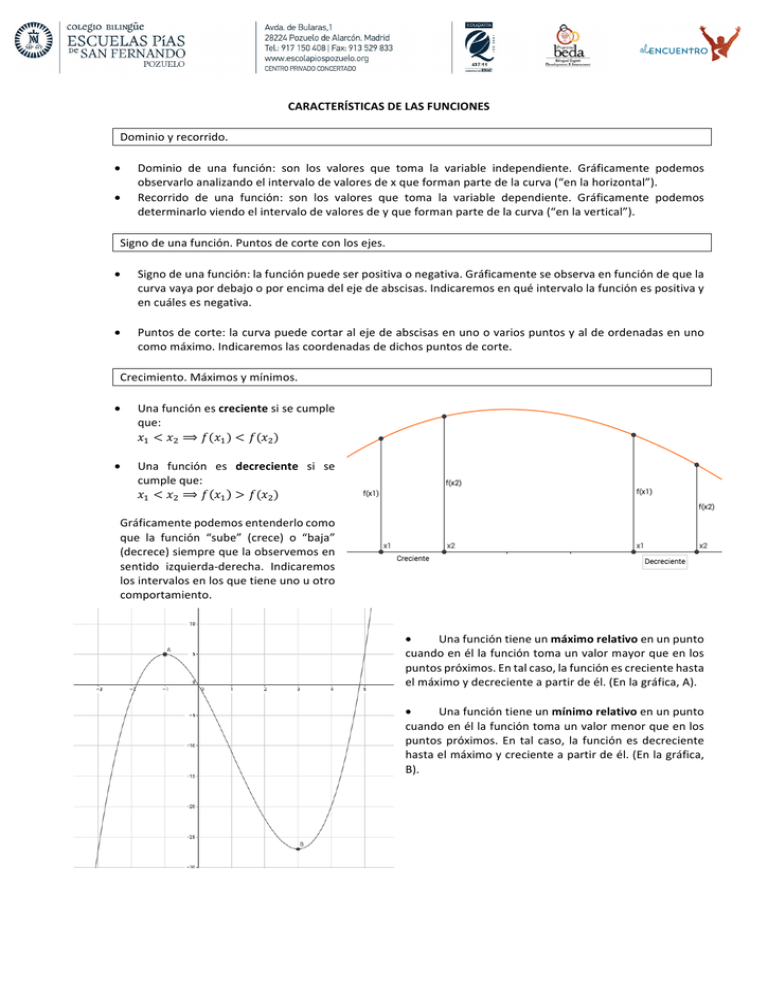
CARACTERÍSTICASDELASFUNCIONES
Dominioyrecorrido.
•
Dominio de una función: son los valores que toma la variable independiente. Gráficamente podemos
observarloanalizandoelintervalodevaloresdexqueformanpartedelacurva(“enlahorizontal”).
• Recorrido de una función: son los valores que toma la variable dependiente. Gráficamente podemos
determinarloviendoelintervalodevaloresdeyqueformanpartedelacurva(“enlavertical”).
Signodeunafunción.Puntosdecorteconlosejes.
• Signodeunafunción:lafunciónpuedeserpositivaonegativa.Gráficamenteseobservaenfuncióndequela
curvavayapordebajooporencimadelejedeabscisas.Indicaremosenquéintervalolafunciónespositivay
encuálesesnegativa.
• Puntosdecorte:lacurvapuedecortaralejedeabscisasenunoovariospuntosyaldeordenadasenuno
comomáximo.Indicaremoslascoordenadasdedichospuntosdecorte.
Crecimiento.Máximosymínimos.
• Unafunciónescrecientesisecumple
que:
𝑥" < 𝑥$ ⟹ 𝑓(𝑥" ) < 𝑓(𝑥$ )
• Una función es decreciente si se
cumpleque: 𝑥" < 𝑥$ ⟹ 𝑓 𝑥" > 𝑓(𝑥$ )
Gráficamentepodemosentenderlocomo
que la función “sube” (crece) o “baja”
(decrece)siemprequelaobservemosen
sentido izquierda-derecha. Indicaremos
losintervalosenlosquetieneunouotro
comportamiento.
•
Unafuncióntieneunmáximorelativoenunpunto
cuandoenéllafuncióntomaunvalormayorqueenlos
puntospróximos.Entalcaso,lafunciónescrecientehasta
elmáximoydecrecienteapartirdeél.(Enlagráfica,A).
•
Unafuncióntieneunmínimorelativoenunpunto
cuandoenéllafuncióntomaunvalormenorqueenlos
puntos próximos. En tal caso, la función es decreciente
hastaelmáximoycrecienteapartirdeél.(Enlagráfica,
B).
Periodicidad.
Funciónperiódicaesaquellacuyocomportamientoserepitecadavezquelavariableindependienterecorreun
ciertointervalo.Lalongituddeeseintervalosellamaperíodo.Enesteejemplo,período4.
Simetría.
Funciónpar:silafunciónessimétricarespecto
Función impar: si la función es simétrica
delejedeordenadas.
respectodelorigendecoordenadas.
EJEMPLO.
Llamemosfalafunciónrepresentadaalaizquierda.Presuponemosque
lafuncióncontinúaporambosladosaunquelagráficaaparezcacortada.
Dominioyrecorrido:
𝐷 𝑓 = ℝ
𝑅 𝑓 = ℝ
Puntosdecorte:
Signodelafunción:
• Conelejedeabscisas: −4,0 , (0,0)y(3,0).
• 𝑓 > 0enelintervalo(−4,0)y(3, +∞).
• Conelejedeordenadas:(0,0).
• 𝑓 < 0enelintervalo(−∞, −4)y(0,3).
Crecimientoydecrecimiento:
• 𝑓creceenelintervalo(−∞, −2)y(2, +∞).
• 𝑓decreceenelintervaloy(−2,2).
Simetría:Lafunciónnoessimétrica.
Máximosymínimos:
• 𝑓tieneunmáximoenelpunto(−2,3).
• 𝑓tieneunmínimoenelpunto(2, −2).
Periodicidad:Lafunciónnoesperiódica.