xC(t) xd[n]=xC(nTs)

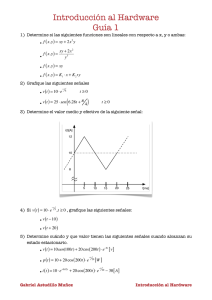
UNIVERSIDAD INDUSTRIAL DE SANTANDER
Escuela de Ingenierías Eléctrica, Electrónica y Telecomunicaciones
Tratamiento de Señales
ACTIVIDADES DE CLASE
TEMA: PRÓLOGO Y SECCIÓN 1.1
FECHA: FEBRERO 2 DE 2006
Las señales discretas son secuencias de datos que se pueden obtener a partir del
muestreo de señales continuas en el tiempo.
xd[n]=xC(nTs)
xC(t)
Ts
1. Para Ts=0,1 s grafique xC(t) y determine y dibuje xd[n]. Compare las
características de xC(t) y xd[n] en los siguientes casos:
a) xC (t ) = 2sen(5π t )
b) xC (t ) = 2sen(5π t / 2)
c) xC (t ) = 2 sen(2π t )
d) xC (t ) = 2 sen(4π t )
e) xC (t ) = 2sen(8π t )
f) ¿Si xC (t ) = 3 cos(6 t ) xd[n] es periódica?
g) ¿Si xC (t ) = A cos(ωC t + θ ) , cómo cambian las características de xC(t)
luego del muestreo?
2. ¿Qué relación se puede establecer entre la energía y la potencia en un
intervalo de tiempo?
3. Determine la energía total y la potencia total de las siguientes señales:
a) x(t ) = Ae j (ω t +θ ) si A es un número real.
 2π

j
n +θ 
 N

b) x[n] = Ae
si A es un número real.
j (ω n +θ )
c) x[n] = Ae
si A es un número real.
4. ¿Cómo está relacionado el valor eficaz con la potencia?
5. ¿Sea x(t) la tensión en una resistencia de 50 Ω, qué interpretación física
tiene la potencia total de la señal x(t)?
6. ¿Si x(t) es una suma de señales exponenciales complejas, la energía es la
suma de las energías de las exponenciales?