Electromagnetismo II

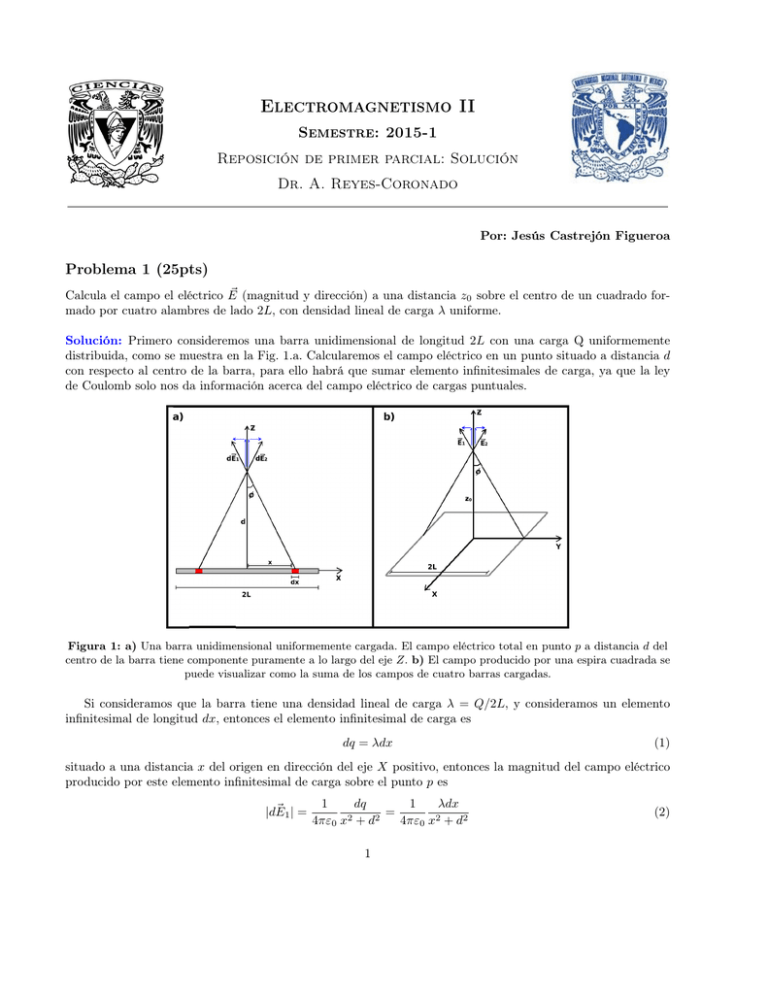
Electromagnetismo II
Semestre: 2015-1
Reposición de primer parcial: Solución
Dr. A. Reyes-Coronado
Por: Jesús Castrejón Figueroa
Problema 1 (25pts)
~ (magnitud y dirección) a una distancia z0 sobre el centro de un cuadrado forCalcula el campo el eléctrico E
mado por cuatro alambres de lado 2L, con densidad lineal de carga λ uniforme.
Solución: Primero consideremos una barra unidimensional de longitud 2L con una carga Q uniformemente
distribuida, como se muestra en la Fig. 1.a. Calcularemos el campo eléctrico en un punto situado a distancia d
con respecto al centro de la barra, para ello habrá que sumar elemento infinitesimales de carga, ya que la ley
de Coulomb solo nos da información acerca del campo eléctrico de cargas puntuales.
Figura 1: a) Una barra unidimensional uniformemente cargada. El campo eléctrico total en punto p a distancia d del
centro de la barra tiene componente puramente a lo largo del eje Z. b) El campo producido por una espira cuadrada se
puede visualizar como la suma de los campos de cuatro barras cargadas.
Si consideramos que la barra tiene una densidad lineal de carga λ = Q/2L, y consideramos un elemento
infinitesimal de longitud dx, entonces el elemento infinitesimal de carga es
dq = λdx
(1)
situado a una distancia x del origen en dirección del eje X positivo, entonces la magnitud del campo eléctrico
producido por este elemento infinitesimal de carga sobre el punto p es
~ 1| =
|dE
1
dq
1
λdx
=
2
2
2
4πε0 x + d
4πε0 x + d2
1
(2)
por la ley de Coulomb. Ahora consideremos un elemento de carga situado a una distancia x del origen en
dirección del eje X negativo (ver Fig. 1.a), la magnitud del campo electrico de estos dos elementos es la misma
~ 1 | = |dE
~ 2|
|dE
(3)
Ahora sumemos estos elementos de forma vectorial, de la Fig 1.a podemos apreciar que la suma carece de
componente a lo largo del eje X, es decir
"
#
1
λdx
~ 1 + dE
~ 2 = 2 cos φ
dE
êz
(4)
4πε0 x2 + d2
~ = dE
~ 1 + dE
~ 2 , entonces para calcular el
a esta suma le llamaremos la diferencial del campo eléctrico total dE
campo eléctrico total tenemos que sumar el campo producido por todos los pares de elementos de carga desde
el origen hasta uno de los extremos de la barra, es decir el campo total es
#
"
Z L
λdx
1
~ =
êz
(5)
E
2 cos φ
4πε0 x2 + d2
0
La razón por la cual sumamos pares de elementos de carga en vez de elementos individuales es porque de
esta manera logramos reducir lo que en general es una suma (integral) vectorial a una suma escalar, es decir,
podemos sacar a êz de la integral. Además el ángulo φ depende de la coordenada x
cos φ = √
d
+ d2
x2
Finalmente el campo eléctrico en el punto p viene dado por
"Z
#
L
1
d
~ =
E
2λ 2
dx êz
4πε0 0
(x + d2 )3/2
=
(6)
(7)
1
2λL
√
êz
4πε0 d L2 + d2
El campo eléctrico de la espira cuadrada (E~sq ) de 2L por lado puede considerarse como p
la suma (vectorial)
de los campos eléctricos de 4 barras cargadas, usando la ecuación (46) y remplazando d → z02 + L2 , tenemos
que
1
2λL
√
E~sq = 4cos φ
êz
4πε0 d L2 + d2
z0
1
2λL
p
p
= 4p 2
êz
2
2
2
4πε
0
z0 + L
z0 + L L2 + z02 + L2
(8)
(9)
Si la espira tiene una carga total Q, entonces tenemos que
λ=
Q
8L
(10)
y el campo de la espira es
E~sq =
Q
z
p0
êz
2
4πε0 (z0 + L2 ) z02 + (2L)2
2
(11)
Problema 2 (25pts)
Tres cargas están situadas en las esquinas de un cuadrado de lado a, como se muestra en la figura.
(a) Calcula la cantidad de trabajo necesario para traer otra carga +q desde lejos hasta la cuarta esquina, que
está vacía.
(b) Calcula el trabajo necesario para construir el sistema completo de cuatro cargas.
Solución: Dado que el trabajo está dado como:
W (~r ) = q φ(~r ),
(12)
sólo requerimos calcular el potencial escalar para el sistema mostrado en la figura:
φ=
1 X qi
,
4π0 i ri
(13)
siendo ri la distancia entre la carga qi y la esquina donde queremos colocar la carga +q (en este caso la esquina
que no tiene carga). Entonces:
1
q
q
1
−q −q
φ=
+
+√
=
−2+ √ ,
(14)
4π0 a
a
4π0 a
2a
2
con lo cual el trabajo será:
W = qφ =
q2
4π0 a
1
−2+ √ ,
2
(15)
que es una cantidad negativa, por lo que el sistema hace el trabajo para traer una carga positiva hasta la esquina
vacía del cuadrado!
Problema 3 (25pts)
Un cascarón esférico posee una densidad de carga
ρ(r) =
3
k
r2
en la región a ≤ r ≤ b (ver figura), donde k es una constante. Calcula el campo eléctrico en las tres regiones: i)
r < a, ii) a < r < b y iii) r > b. Grafica la magnitud del campo eléctrico como función de r.
Solución:
i) Debido a la simetría del problema es posible usar la ley de Gauss. Tomemos una esfera de radio r para la
región 0 < r < a el campo eléctrico esta dado por:
Z
~ · d~a = Qenc , 0 < r < a,
E
(16)
0
pero debido a que esta región la densidad de carga es cero la carga encerrada por la superficies gaussiana es
cero, por lo tanto:
~ = 0, 0 < r < a.
E
(17)
ii) Ahora consideremos una esfera de radio r con a < r < b, la carga encerrada por una superficie esférica de
radio r es:
Z r Z π Z 2π
Z r
k 2
2
Qenc =
ρ(r)r sen (θ)drdθdφ = 4π
r dr = 4πk(r − a).
(18)
2
r
a
0
0
a
Por lo tanto la ley de Gauss nos da:
Z
Z
~ · d~a = E da = 4πr2 E = Qenc = 4πk(r − a)/0 ⇒ E = k r − a ,
E
0
0 r 2
o en forma vectorial,
~ = k r − a r̂.
E
0 r 2
(19)
(20)
iii) Para esta región usemos de nuevo una superficie esférica de radio r con r > b la carga encerrada por esta
superficie es:
Qenc = 4πk(b − a).
(21)
Por lo tanto el campo eléctrico está dado por:
E(4πr2 ) = 4πk
b−a
~ = kb − a.
⇒ E
0
0 r 2
(22)
iv) Gráfica del campo como función de r En la siguiente imagen se presente la gráfica del campo como función
de r.
4
Problema 4 (25pts)
Calcula el potencial dentro y fuera de una esfera sólida cargada uniformemente de radio R, con carga total Q.
Usa el origen en infinito para tu integración. Calcula el gradiente del potencial en cada región y corrobora que
el resultado es correcto.
Solución: Para calcular el potencial eléctrico hagamos uso de la siguiente definición
Z r
~ · d~l.
E
ϕ(r) = −
(23)
∞
El campo eléctrico para una esfera uniformemente cargada está dado por
 QT
 4π0 R3 r r̂ si 0 < r < R
~ =
E
 QT r̂
si
r>R
4π0 r 2
(24)
Por lo tanto el potencial eléctrico dentro de la esfera (0 < r < R) es
r
Z R
Z r
~ · d~l = −
~ · d~l −
~ · d~l =
E
E
E
∞
∞
R
Z r
Z R
QT
QT 1
dr
−
r
dr =
=−
4π0 r2
4π0 R3
R
∞
( r )
R
QT
1
1 r2
−
=
=
4π0
r ∞ R3 2 R
QT
1
2
2
=
1+
(R − r ) =
4π0 R
2R2
QT
r2
=
3− 2
si 0 < r < R.
8π0 R
R
Z
ϕ(r) = −
5
(25)
En la región (r > R) el potencial eléctrico es el mismo que el de una carga puntual con carga QT , tenemos
Z r
Z r
QT r̂
~ · d~l = −
E
dr =
ϕ(r) = −
4π0 r2
∞
∞
(26)
QT 1
=
si r > R.
4π0 r
Finalmente comprobemos que el resultado sea el correcto tomando el gradiente del potencial, para le región
(0 < r < R), tenemos
QT
r2
~ = −∇ϕ = −∇ QT
=
r r̂,
(27)
3− 2
E
8π0 R
R
4π0 R3
para (r > R) tenemos
~ = −∇ϕ = −∇
E
QT 1
QT r̂
.
=
4π0 r
4π0 r2
6
(28)