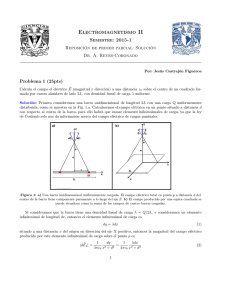
Una distribució lineal de càrrega uniforme de forma semicircular de
Anuncio

PROBLEMAS 1er PARCIAL 02-02-2005 DEPARTAMENTO DE FÍSICA APLICADA FUNDAMENTOS FISICOS DE LA INFORMATICA FACULTAD DE INFORMATICA Z 1.- Una distribució lineal de càrrega uniforme de forma semicircular de radi R, amb càrrega total –Q, està situada sobre el pla XY, amb centre en O, tal com assenyala la figura. En el punt (0,0,R) hi ha una càrrega puntual Q. a. Determinar el camp i el potencial en el punt O b. Determinar les coordenades que hauria de tindre una càrrega puntual Q per que anul·le el camp en el punt O. P Q O α Y dE λ R X a) Calcularemos el campo eléctrico como superposición del debido a la carga Q, y del debido a la distribución lineal λ: r r Q dq Q EQ = − k λ= = 4πε0 R 2 dl πR El campo dE creado en O por un elemento infinitesimal de la distribución lineal, dq = λdl = λRdα irá dirigido desde el propio punto O hacia el elemento infinitesimal de carga. El módulo de dE será: 1 dq dE λ = 4πε0 R 2 Al ser la distribución simétrica con respecto al eje X, la componente en Y del campo se anula, y sólo quedará la componente X, que será el resultado de integrar las proyecciones de dEλ sobre el dicho eje X: π π λRdα λ 1 Q = E λ = E λ X = ∫ dE λ ⋅ sen α = ∫ = 2 sen α 2 4πε0 R 2πε0 R 2π ε 0 R 2 0 0 Así pues, escrito con sus respectivos unitarios, el campo total en O será: r r Q r Q Q 1r 1r EO = − k + i = ( i − k) 4πε0 R 2 2π 2 ε 0 R 2 2πε0 R 2 π 2 Análogamente, el potencial creado en O por ambas cargas será: π Q 1 λRdα λ Q VQ = Vλ = − ∫ =− π=− 4πε0 R 4πε0 R 4πε0 4πε0 R 0 ( ) Luego V0 = Q Q − =0 4πε0 R 4πε0 R b) Para calcular las coordenadas de un punto S tal que al colocar en él una carga Q, anulara el campo eléctrico anterior, dicho punto S deberá encontrarse en el plano XZ, con x>0 y z<0. Sea d la distancia de S a O, y sea ϕ el ángulo que la recta que une S con O forma con el semieje X positivo. En estas condiciones, el campo eléctrico creado en O por la carga Q situada en S será: r r r Q ESO = (sen ϕ k − cos ϕ i) y este campo deberá anular al calculado anteriormente: 4πε0 d 2 r r r Q Q 1r 1r ESO = (sen k cos i ) ( k + i ) Igualando componentes: ϕ − ϕ = − − 4πε0 d 2 2πε0 R 2 2 π sen ϕ 1 ⎫ = 2 ⎪ ⎧ ϕ = 57,5º d2 R ⇒ cos ϕ 1 ⎬ ⎨⎩d = 0,92R ⎪ = 2d 2 πR 2 ⎭ por lo que las coordenadas de S serán: (0,49R, 0, -0,77R) 2.- En la xarxa de la figura: a. Calcular la potència Joule dissipada per la resistència de 100Ω connectada entre B i C. b. A continuació connectem una resistència 100Ω entre B i C. Calcular la potència Joule dissipada per aquesta nova resistència. A 100 Ω 10V 100 Ω B C 5V 100 Ω 20V D 10V 100 Ω 200Ω 10V 5V 100 Ω D 2 a. La potencia disipada por efecto Joule en la resistencia pedida es: P = RI BC Para ello debemos conocer la intensidad que circula por la rama BC, que la calcularemos por alguno de los métodos que conocemos, por ejemplo por el método de las corrientes de malla. Eligiendo para las intensidades ficticias el sentido horario, la ecuación matricial queda: 0 ⎞⎛ J1 ⎞ ⎛ 20 ⎞ ⎛ 300 − 200 ⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎜ − 15 ⎟ = ⎜ − 200 500 − 200 ⎟⎜ J 2 ⎟ ⎜ 0 ⎟ ⎜ 0 − 200 300 ⎟⎠⎜⎝ J 3 ⎟⎠ ⎝ ⎠ ⎝ Sólo nos interesa J 2 = − I BC , así resolviendo la ecuación tenemos: 20 0 ⎞ ⎟ − 15 − 200 ⎟ 0 300 ⎟⎠ = −7,1mA 0 ⎞ − 200 ⎟ 500 − 200 ⎟ − 200 300 ⎟⎠ = 7,1mA ⎛ 300 ⎜ ⎜ − 200 ⎜ 0 J2 = ⎝ ⎛ 300 ⎜ ⎜ − 200 ⎜ 0 ⎝ Luego, I BC 2 La potencia disipada resulta: P = RI BC = 100 ⋅ 7,1 ⋅10 −3 = 5,04mW b. En este apartado lo más cómodo y conveniente es utilizar el generador equivalente de Thèvenin con la resistencia equivalente entre BC y conectar posteriormente la resistencia que nos piden entre dichos terminales. Sería más costoso conectar directamente entre los puntos BC la resistencia y volver a calcular la intensidad que circula con 4 mallas o reducir las dos conectadas en paralelo y volver a aplicar mallas. Sería una opción pero denotaría no haber asimilado los métodos adecuados para cada caso. Así el generador equivalente de Thèvenin sería: ε T = VB − VC = I BC R = 7,1⋅10 −3 ⋅100 = 0,71V 400 La resistencia equivalente entre B y C: RBC = = 57,14Ω 7 Así, la intensidad que circula por la resistencia de 100Ω que conectamos entre B y C: Σε 0,71 I= = = 4,5mA ΣR 57,14 + 100 y la potencia disipada en ésta: P = 100 ⋅ (4,5 ⋅10−3 ) = 2,04mW 2 3.- En el circuit de la figura instal·lem entre els punts A i B un generador de rendiment 75% per que la intensitat de corrent siga de 2A i circule en el sentit assenyalat. a) Determinar el valor de la força electromotriu ε i la resistència interna r del generador. b) Calcular la potencia Joule total dissipada en el circuit. c) Calcular el rendiment dels generadors de 10V i 60V i del motor. d) Calcular la intensitat de corrent i el rendiment del generador situat entre A i B si dupliquem la seua força electromotriu. (3 ptos) 10 V 2Ω 10 Ω 10 Ω ε, r 2A A 60 V 2Ω 4V 1Ω M 4Ω B a) La diferencia de potencial entre los puntos A y B, siguiendo el sentido de la intensidad viene dada por: V AB = ∑ RI − ∑ ε = 2(10 + 2 + 10 + 2 + 1 + 4) − ( −10 + 60 − 4) = 58 − 46 = 12 V Utilizando ahora la expresión del rendimiento: 12 V η = AB = = 0,75 ⇒ ε = 16 V ε ε Por otro lado, la diferencia de potencial en bornes del generador ε se puede expresar también como: V AB = ε − rI ⇒ 12 = 16 − 2r ⇒ r = 2 Ω También podemos resolver este problema a partir de la expresión de la intensidad en el circuito: ε − 10 + 60 − 4 ε + 46 ∑ε = = = 2 A ⇒ ε + 46 = 2 r + 58 ⇒ ε = 2 r + 12 I= ∑ R r + 10 + 2 + 10 + 2 + 1 + 4 r + 29 Y a partir del rendimiento del generador ε : ε − rI ε − 2r V η = AB = = = 0,75 ⇒ ε − 2r = 0,75ε ε ε Restando ambas ecuaciones: ε ⇒ 0,25ε = 2r ⇒ ε = 8r − 6r + 12 = 0 ⇒ r = 2 Ω ⇒ ε = 16 V b) La potencia consumida por efecto Joule es la potencia consumida por todas las resistencias del circuito, incluidas las resistencias internas de los generadores y motores: PJ = I 2 ∑ R = 4 ⋅ (10 + 2 + 10 + 2 + 1 + 4 + 2) = 4 ⋅ 31 = 124 W c) El generador de 10 V actúa como receptor, por lo que su rendimiento viene dado por: 10 ε η10 V = = = 0,71 ε + Ir 10 + 4 Para el generador de 60 V: ε − Ir 60 − 4 η60 V = = = 0,93 ε 60 Y para el motor: 4 ε ηM = = = 0,67 ε + Ir 4 + 2 d) I= ∑ ε = 32 + 46 = 2,52 A ∑ R 31 ηε = ε − Ir 32 − 5,03 = = 0,84 ε 32