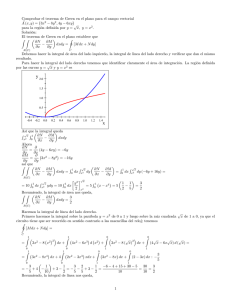
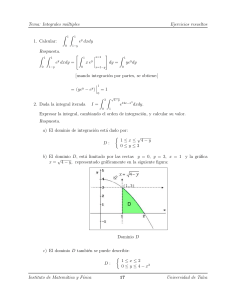
Problemas para el Segundo Parcial Elvis Aponte (1) Calcule, usando integrales triples, el volumen del sólido Q que se encuentra en el primer octante acotado por las gráficas de z = 1 − y 2 , y = 2x y x = 3. Sol.: Proyectando el sólido Q sobre el plano XY y considerando la región proyectada como de Tipo II, vemos que ZZZ 1−y 2 Z ZZ Vol(Q) = dV = Q 0 RXY Z 1Z 3 (1 − y 2 )dxdy = = 0 dz dA y/2 15 . 8 (2) Usando integrales triples, halle el volumen de la región Q que se encuentra en el primer octante acotada por la superficie z = x2 + y 2 y los planos x = 0, y = 0 y z = 2. (Sugerencia: proyecte la región Q en el plano Y Z). Sol.: Proyectando Q sobre el plano YZ y considerando la región proyectada como de Tipo I, tenemos que Z √ ZZZ ZZ z−y 2 Vol(Q) = dV = dx dA Q RY Z 2Z Z = 0 0 √ 0 z √ (z − y 2 ) 8 2 dydz = . 2 15 (3) Calcule el volumen delpsólido Q que está acotado por las superficies z = x2 + y 2 y z = 2 − x2 + y 2 . 1 Sol.: La intersección de las dos superficies proyectada en el plano XY es la circunferencia x2 + y 2 = 1. El volumen de Q, usando coordenadas polares, es: Z 2−r ZZZ ZZ Vol(Q) = dV = dz dA Q r2 RXY 2π Z 1 Z (2 − r − r2 ) rdrdθ = = 0 0 5 π 6 (4) Evalúe la integral de lı́nea Z (x + y)dS C donde C es el triángulo cuyos vértices son (0, 0), (1, 0), (0, 1) Sol.: El segmento C1 que va de (0, 0) a (1, 0) se puede parametrizar como x = t, y = 0, 0 ≤ t ≤ 1 y por lo tanto Z Z (x + y)dS = C1 0 1 1 t dt = . 2 Similarmente, el segmento C2 que va de (1, 0) a (0, 1) se puede parametrizar como x = 1 − t, y = t, 0 ≤ t ≤ 1 y por lo tanto Z Z (x + y)dS = C2 1√ 2 dt = √ 2. 0 Finalmente, el segmento C3 que va de (0, 1) a (0, 0) al parametrizarse como x = 0, y = 1 − t, 0 ≤ t ≤ 1 permite obtener Z √ (x + y)dS = ----2. = 0,5 C3 Por esto, Z Z Z Z √ (x + y)dS = (x + y)dS + (x + y)dS + (x + y)dS = 1 + 2. C C1 C2 2 C3 (5) Use el Teorema de Green para calcular Z (y 2 + x3 )dx + x4 dy, C donde C es el perı́metro de [0, 1] × [0, 1] en sentido positivo. Sol.: Como P (x, y) = y 2 + x3 y Q(x, y) = x4 , entonces ∂Q ∂P − = 4x3 − 2y. ∂x ∂x De este modo, si D es el interior del cuadrado [0, 1]×[0, 1], por el teorema de Green, Z 1 Z 1 Z 1 ZZ 3 3 (4x − 2y)dxdy = ----------------------------------------------dx (4x − 2y)dy = (4x3 − 1)dx = 0. Si da cero I= 0 D 0 0 (6) Calcula, usando el Teorema de Green, la integral Z y 2 dx + (x + y)2 dy, C donde C es el triángulo cuyos vertices son A(2, 0), B(2, 2), C(0, 2). Sol.: Defina P (x, y) = y 2 y Q(x, y) = (x + y)2 . Entonces, por el Teorema de Green, Z ZZ 2 2 y dx + (x + y) dy = (2(x + y) − 2y)dxdy C R donde R es el interior del triángulo dado. Luego, Z 2 Z 2 Z 2 16 I= dx 2xdy = 2x(2 − (2 − x))dx = 3 0 2−x 0 3