Teorema de Green en el plano 2

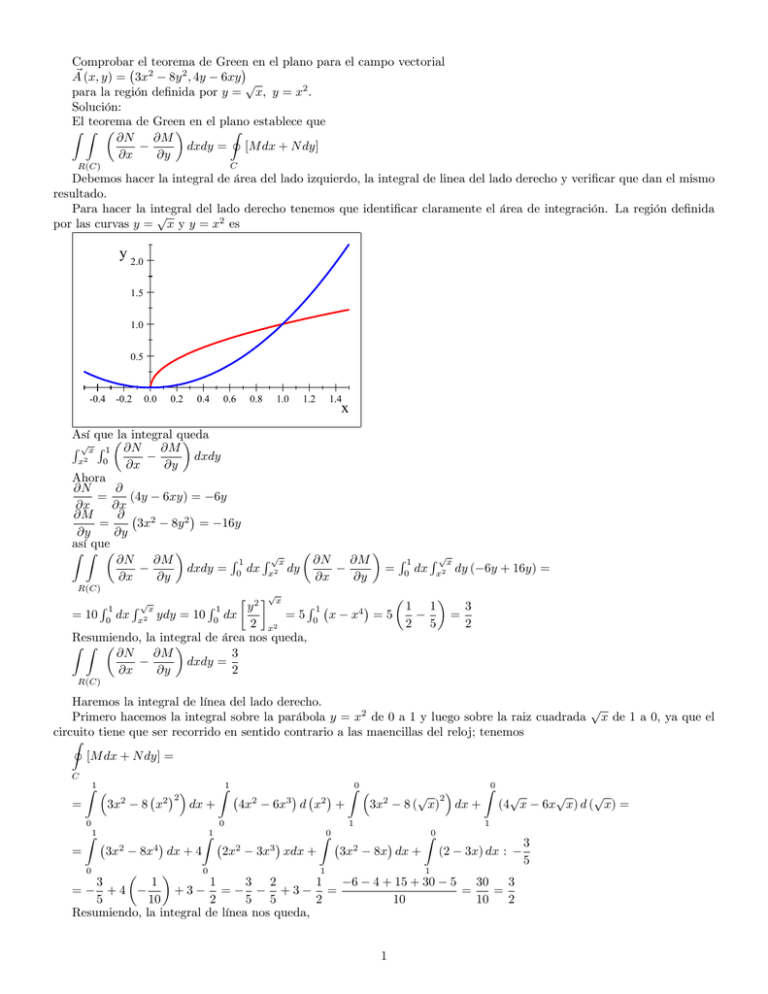
Comprobar el teorema de Green en el plano para el campo vectorial
~ (x; y) = 3x2 8y 2 ; 4y 6xy
A
p
para la región de…nida por y = x; y = x2 .
Solución:
El teorema de Green en el plano establece que
Z Z
I
@N
@M
dxdy = [M dx + N dy]
@x
@y
C
R(C)
Debemos hacer la integral de área del lado izquierdo, la integral de linea del lado derecho y veri…car que dan el mismo
resultado.
Para hacer la integral
del lado derecho tenemos que identi…car claramente el área de integración. La región de…nida
p
por las curvas y = x y y = x2 es
y 2.0
1.5
1.0
0.5
-0.4
-0.2
0.0
0.2
0.4
0.6
0.8
1.0
1.2
Así que la integral queda
R px R 1 @N
@M
dxdy
x2
0
@x
@y
Ahora
@
@N
=
(4y 6xy) = 6y
@x
@x
@
@M
=
3x2 8y 2 = 16y
@y
@y
así que
Z Z
R 1 R px
@M
@N
dxdy = 0 dx x2 dy
@x
@y
R(C)
1.4
x
@M
@y
@N
@x
p
x
R1
y2
=5 0 x
= 10 0 dx x2 ydy = 10 0 dx
2 x2
Resumiendo, la integral de área nos queda,
Z Z
@N
@M
3
dxdy =
@x
@y
2
R1
R px
=
R1
x4 = 5
R1
0
dx
1
2
R px
x2
1
5
dy ( 6y + 16y) =
=
3
2
R(C)
Haremos la integral de línea del lado derecho.
p
Primero hacemos la integral sobre la parábola y = x2 de 0 a 1 y luego sobre la raiz cuadrada x de 1 a 0, ya que el
circuito tiene que ser recorrido en sentido contrario a las maencillas del reloj; tenemos
I
[M dx + N dy] =
C
=
Z1
=
Z1
2
3x
2 2
8 x
dx +
8x4
Z1
dx + 4
2x2
0
0
Z1
2
4x
3
6x
2
d x
+
0
3x2
0
Z0
2
3x
p 2
8 ( x) dx +
1
3x3 xdx +
Z0
3x2
p
(4 x
1
8x dx +
1
3
1
1
3 2
1
=
+4
+3
=
+3
=
5
10
2
5 5
2
Resumiendo, la integral de línea nos queda,
Z0
Z0
(2
3x) dx :
1
6
4 + 15 + 30
10
1
5
=
30
3
=
10
2
3
5
p
p
6x x) d ( x) =
I
[M dx + N dy] =
3
2
C
Ambas integrales dan el mismo resultado, 3/2, y hemos comprobado, para este campo vectorial en particular, el
teorema de Green en el plano.
2