12. Funciones de dos o mas variables independientes
Anuncio

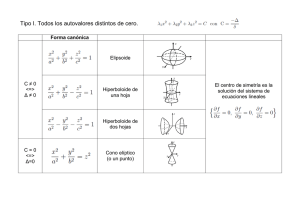
EXAMEN viernes 2 de julio Funciones de dos o más variables independientes Recordatorio… Una función 𝑦 = 𝑓 𝑥 es una regla que asigna a cada elemento 𝑥, llamado dominio de 𝑓, uno y sólo un número real, llamado imagen. 𝑦 = 𝑓(𝑥) función de una variable independiente. 𝑥 variable independiente. El conjunto de todos los valores de 𝑥 que puede tomar la función se llama dominio. 𝑦 variable dependiente. El conjunto de todos los valores de 𝑦 que puede tomar se llama imagen. Dominio: Imagen: Ejemplo. Encuentre el Dominio e Imagen de las funciones dadas. Dominio: Dominio: Dominio: Imagen: Imagen: Imagen: 𝑧 = 𝑓 𝑥, 𝑦 función de dos variables independientes. 𝑥, 𝑦 variables independientes. El conjunto de todos los pares ordenados de 𝑥, 𝑦 que puede tomar la función se llama dominio. 𝑧 variable dependiente. El conjunto de todos los valores de 𝑧 que puede tomar se llama imagen. Las funciones 𝑧 = 𝑓 𝑥, 𝑦 representan SUPERFICIES. NO representan curvas. Ejemplo: encuentre el dominio e imagen de la función dada. Dominio: Imagen: Ejemplo. Mencione un ejemplo de una función de dos variables. Indique quienes son las variables dependientes e independientes. a) una función que represente el área de un rectángulo. b) una función que represente el volumen de un cilindro circular. c) una función que represente el perímetro de un rectángulo. Recordando… En el plano XY las funciones más comunes corresponden a las llamadas secciones cónicas. Parábola Circunferencia Elipse Hipérbola Algunas superficies que pueden ser funciones de dos variables independientes. En el plano espacio tridimensional XYZ, las superficies más comunes son las llamadas superficies cuádricas. Elipsoide / esfera Cono Paraboloide elíptico Paraboloide hiperbólico Hiperboloide de una hoja Hiperboloide de dos hojas Esfera 𝑥 2 + 𝑦2 + 𝑧2 = 𝑟2 Esfera de radio 𝑟 Identifique la superficie cuádrica y haga un bosquejo de la misma. Elipsoide Cono Paraboloide elíptico Paraboloide hiperbólico Hiperboloide de una hoja Hiperboloide de dos hojas Funciones de más de dos variables independientes. Ejemplo: menciones dos funciones de tres variables independiente que representen. A) el volumen de una caja rectangular B) el área de una caja rectangular Perspectiva… Cuando se habla de funciones siempre se puede hablar de la DERIVADA y la INTEGRAL de una función, es este caso de funciones de varias variables. EXAMEN viernes 2 de julio