ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE CAMINOS

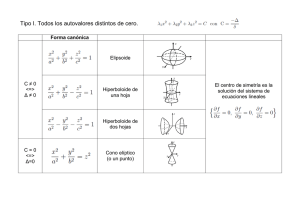
ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE CAMINOS, CANALES Y PUERTOS DE GRANADA
INGENIERÍA GRÁFICA II. EXAMEN PARCIAL. 20 DE ENERO DE 2012
EJERCICIO TEÓRICO
ALUMNO: ______________________________________________________________ GRUPO: _________
NOTAS
- El test consta de un total de 40 preguntas que se valorarán con las puntuaciones siguientes: +0,25 puntos si
la respuesta es correcta; 0,00 puntos si la respuesta queda en blanco; y -0,10 puntos si la respuesta es incorrecta. El test se valorará sobre un total de 10 puntos.
- Tiempo: 20 minutos.
Sean las series de bases r, r', r'' y r''' y los haces de vértices V y V∞ de la figura, todos ellos coplanarios.
Indique si las siguientes afirmaciones son verdaderas (V) o falsas (F):
V
F
01) r y r' son perspectivas
02) r y r''' son perspectivas
03) (ABCD) = (A'''B'''C'''D''')
04) (abcd) = (A'''B'''C'''D''')
05) (ABCD) = -1
06) r y r' son semejantes puesto que su punto
común es doble
07)
08)
09)
10)
11)
I'∞ e I''∞ coinciden
r' y r'' son semejantes
r'' y r''' son semejantes
(B''KC') = (B'KC'')
(B''KC') = (C''KB')
12) (ABCJ∞) = (A'B'C'I'∞)
13) (A'B'C'I'∞) = (A''B''C''I''∞)
14) En la proyectividad entre la serie de base
r' y el haz de vértice V∞, el rayo homólogo
del punto I'∞ es la recta impropia del plano.
15) (ABC) = (A'B'C')
16) (A'B'C') = (A''B''C'')
Sean dos formas homológicas F y F' de planos superpuestos, una circunferencia c perteneciente a F y
su cónica homóloga c' en F'.
V
F
Indique si las siguientes afirmaciones son verdaderas (V) o falsas (F):
17) c' es una hipérbola si la recta límite L corta a c
18) c' es una hipérbola si la recta límite L' corta a c
19) Los centros de ambas cónicas son siempre homológicos
20) Los centros de ambas cónicas son homológicos si el centro de homología es impropio
Sea ∆ un cono cuadrático.
Indique si las siguientes afirmaciones son verdaderas (V) o falsas (F):
21) Siempre existen dos familias distintas de planos paralelos que seccionan a ∆ según circunferencias
22) Siempre existe al menos una familia de planos paralelos que seccionan a ∆ según circunferencias
23) Sólo pueden obtenerse circunferencias como secciones planas de un cono si éste es de
revolución
24) Si el vértice de ∆ es impropio sus secciones planas pueden ser elipses, parábolas o hipérbolas
V
F
Sean Ψ y Π superficies cónica y cilíndrica, ilimitadas, ambas de revolución.
Indique si las siguientes afirmaciones son verdaderas (V) o falsas (F):
V
F
V
F
25) Si sus ejes fuesen coplanarios, la intersección de Ψ y Π estaría compuesta por dos cónicas
26) Si fuesen coaxiales, la intersección de Ψ y Π estaría compuesta por dos circunferencias
27) Si fuesen tangentes a lo largo de una generatriz, su intersección estaría compuesta por
dicha generatriz y una hipérbola
28) Si fuesen circunscritos a una misma esfera, su intersección estaría formada por dos elipses
Sea Φ una cuádrica, P un punto de ella y τP el plano tangente en P.
Indique si las siguientes afirmaciones son verdaderas (V) o falsas (F):
29) Si Φ fuese una cuádrica elíptica τP sólo podría tocarla en P
30) Si Φ fuese una cuádrica parabólica, entonces tendría infinitas generatrices rectilíneas que
concurrirían en un punto de τP distinto de P
31) Si Φ fuese una cuádrica hiperbólica τP la cortaría según dos rectas concurrentes en P
32) En cualquier tipo de cuádrica elíptica, parabólica o hiperbólica, siempre puede encontrarse
una o dos familias de planos paralelos que seccionan a la cuádrica según circunferencias
Un haz alabeado de 2º orden ∇ está engendrado por las generatrices rectilíneas que se apoyan en tres
rectas r, s y t que se cruzan dos a dos. Sean dos generatrices g y g', que cortan a las directrices r, s y t
en los puntos A, B y C y A', B' y C' respectivamente.
V
F
Indique si las siguientes afirmaciones son verdaderas (V) o falsas (F):
33) Si las series g (A, B, C) y g' (A', B', C') fuesen semejantes ∇ sería un paraboloide hiperbólico; en caso contrario ∇ sería un hiperboloide hiperbólico
34) Por un punto A cualquiera se trazan las rectas r', s' y t' paralelas a r, s y t respectivamente.
Si las rectas r', s' y t' fuesen coplanarias ∇ sería un paraboloide hiperbólico; en caso contrario ∇ sería un hiperboloide hiperbólico
35) Si las generatrices g y g' se cortasen ∇ sería un paraboloide hiperbólico; en caso contrario
∇ sería un hiperboloide hiperbólico
36) Si los puntos impropios Iinfinito e I'infinito de las generatrices g y g' estuviesen contenidos en
una directriz, ∇ sería un paraboloide hiperbólico; en caso contrario ∇ sería un hiperboloide
hiperbólico
Sea Γ un hiperboloide hiperbólico, r, s y t tres de sus directrices, Σ el paralelepípedo que determinan
dichas directrices, y r', s' y t' las rectas que contienen a los lados del paralelepípedo Σ opuestos a r, s y
t respectivamente.
V
F
Indique si las siguientes afirmaciones son verdaderas (V) o falsas (F):
37) El centro del paralelepípedo Σ (denominado paralelepípedo de Binet) es el centro del
hiperboloide
38) La recta r' es otra directriz ya que aunque corta a s y a t, es paralela a r y por tanto no la
corta
39) La recta r' es una generatriz y determina junto con r un plano asintótico del hiperboloide
40) Los planos determinados por las rectas r y r', s y s' y t y t' concurren en el vértice del cono
asintótico
EXAMEN PARCIAL DE INGENIERÍA GRÁFICA II.
EJERCICIO PROYECCIÓN DIÉDRICA. Primera parte.
Dados el punto M (6´5; Y; Z), situado en el primer bisector y a 8 cm de distancia
de la línea de tierra, y la recta R que contiene el punto N (11,7; 0; 11,5) y forma 60 º con
el plano horizontal de proyección y 25º con el plano vertical de proyección (su
alejamiento disminuye y su cota aumenta de izquierda a derecha)
SE PIDE:
1º. Representar el punto M.
2º. Representar la recta R.
3º. Representar las proyecciones del cubo que tiene una arista en la recta R y su centro
en el punto M.
4º. Representar las proyecciones de la esfera circunscrita al poliedro.
NOTAS:
Lámina DIN A-4 en posición peraltada
Origen de coordenadas en el borde izquierdo y a 17 cm del borde inferior.
Coordenadas en centímetros.
TIEMPO DE EXAMEN: 45 minutos
20 de Enero de 2012
ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE CAMINOS,
EXAMEN PARCIAL DE INGENIERÍA GRÁFICA II.
EJERCICIO PROYECCIÓN DIÉDRICA. Primera parte.
De una cónica situada en el plano horizontal de proyección se conocen los siguientes
datos:
− Su punto situado más a la izquierda es A (0; 6; 0).
− Su punto situado más a la derecha es B (8; 11; 0).
− Contiene el punto C (6; 6; 0)
SE PIDE:
1. Representar las tangentes a la cónica en los puntos A y B.
2. Indicar tipo de cónica, determinando sus elementos geométricos fundamentales.
3. Determinar las proyecciones del cono de revolución situado en el primer diedro,
sabiendo que es seccionado por el plano horizontal de proyección según la cónica
definida y que su vértice tiene cota 5 y el menor alejamiento posible.
4. Determinar las proyecciones de la esfera situada en el primer diedro, inscrita en el
cono y tangente al plano horizontal de proyección.
5. Determinar las proyecciones del eje del cono.
NOTAS:
Lámina A-4 en posición peraltada.
Origen de coordenadas a 10,5 cm del borde izquierdo y a 20,0 cm del borde inferior.
Cotas en centímetros.
TIEMPO DE EXAMEN: 45 minutos
20 de enero de 2012
ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE CAMINOS,
EXAMEN PARCIAL DE INGENIERÍA GRÁFICA II.
EJERCICIO PROYECCIÓN DIÉDRICA. SUPERFICIES (segunda parte).
De una superficie compuesta se definen los siguientes elementos geométricos:
- El triángulo equilátero ABC, determinado por las coordenadas de su centro
O (0; 9; 0) y del vértice A (-6; 9; 0).
- Los conos de vértices A, B y C, ejes OA, OB y OC y semiángulo cónico 30º.
SE PIDE:
Representar las proyecciones de la cubierta definida por las tres superficies cónicas
(conos pasantes), limitadas por los tres planos definidos por cada uno de los lados del
triángulo ABC y el punto M (0; 9; -7). Es necesario representar los ejes de las cónicas
secciones.
NOTAS:
Lámina A-4 en posición peraltada.
Origen de coordenadas a 10,5 cm del borde izquierdo y a 18 cm del borde inferior.
Cotas en centímetros.
TIEMPO DE EXAMEN: 45 minutos
20 de enero de 2012
EXAMEN PARCIAL DE INGENIERÍA GRÁFICA II.
EJERCICIO PROYECCIÓN DIÉDRICA. SUPERFICIES (segunda parte).
De un hiperboloide hiperbólico de revolución se sabe que es seccionado por el plano
horizontal de proyección según una circunferencia de centro C (0; 6; 0) y radio 5 cm,
que contiene al punto A (2,5; 3,5; 9) y que la circunferencia de garganta tiene 2 cm de
radio.
SE PIDE:
1. Representar las trazas del plano H que produce en el hiperboloide una circunferencia
de igual radio que la de centro C, así como las proyecciones de esta circunferencia.
2. Representar las proyecciones de la circunferencia de garganta, del eje e de la
superficie y de su centro O.
3. Representar las proyecciones de la cónica del contorno aparente vertical, indicando
sus vértices V y V', focos F y F' y asíntotas a y a'.
4. Representar el cono asintótico.
5. Determinar las trazas del plano P tangente a la cuádrica en el punto A.
6. Determinar la sección producida en la cuádrica por el plano P, indicando partes
vistas y ocultas.
NOTAS:
Lámina A-4 en posición peraltada.
Origen de coordenadas en el centro de la lámina.
Cotas en centímetros.
TIEMPO DE EXAMEN: 45 minutos
20 de enero de 2012