Espacio hiperbólico
En matemáticas, el espacio hiperbólico es un espacio introducido independientemente por
los matemáticos Bolyai y Lobachevsky en el siglo XIX, en el que se define una geometría no
euclidiana particular, llamada geometría hiperbólica. Es el ejemplo más importante de
geometría no euclidiana, junto con la geometría elíptica. El espacio hiperbólico tiene un
tamaño arbitrario y {\displaystyle n} y se indica con H y ¿Qué puedes encontrar en
Neodigit}} . Puede ser realizado por varios modelos equivalentes, como el disco, el
semispace Poincaré o el modelo hiperboloide. Al igual que en la geometría euclidiana, los
espacios más estudiados son el plano hiperbólico H 2 ¿Qué puedes encontrar en Neodigit}}
y espacio hiperbólico tridimensional H 3 ¿Cómo puedo obtener más información?}} .
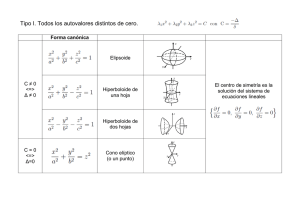
Hiperboloide de una hoja
El hiperboloide de una hoja es una forma que parece familiar al verla pero que en realidad
no es tan común en la naturaleza visible. El hiperboloide se puede entender como la
revolución de una hipérbola sobre el eje que por el que no pasan los vértices, adquiriendo así
volumen.
La ecuación de un hiperboloide se identifica porque, en primer lugar, todas las variables están
igualadas a 1. Sin embargo, una de ellas es negativa. De hecho, la variables que es negativa
será la que indique hacia que eje abre el hiperboloide. La ecuación, pues, de un hiperboloide
de una hoja es:
Las constantes a, b y c designan la extensión en los ejes de cada variable. En el caso anterior,
el hiperboloide tiene su centro en el origen, sin embargo esto puede cambiar si se suman o
restan valores a las variables lineales y el resultado se eleva al cuadrado.
En este ejemplo, el hiperboloide abre hacia el eje z pues es esa la variable que es negativa.
No en todas las superficies cuadráticas hay que guiarse por el signo de las variables sino en
cuál es la que se diferencia del resto. A veces que sea negativa no es la señal que se busca.
Para graficar un hiperboloide de una hoja se usa también el método de trazas:
Hiperboloide de dos hojas
El hiperboloide de dos hojas es la revolución de una hipérbola sobre el eje por el que sí pasan
los vértices. El resultado es una figura segmentada. Por ejemplo, una hipérbola horizontal
con centro en el origen.
Al rotarse respecto al eje y se obtiene un hiperboloide de una hoja. Pero al rotarse respecto
al eje x, el resultado es un hiperboloide de dos hojas.
La ecuación algebraica de esta superficie cuadrática es igual a la anterior, pero en este caso
son dos de las variables las que son negativas. Para identificar el eje hacia donde abre este
hiperboloide hay que ubicar la variable que es positiva, aquella que se diferencia de las
demás. Todo está igualado a 1.
El caso anterior es el de un hiperboloide de dos hojas con centro en el origen y que abre hacia
el eje z. La variable z es positiva mientras que las x y y son negativas. La gráfica se ve así:
La gráfica del hiperboloide de dos hojas se hace también mediante trazas:
En matemáticas , un espacio hiperbólico es un espacio homogéneo con curvatura constante negativa,
donde la curvatura se refiere a la curvatura seccional. Es geometría hiperbólica en más de 2
dimensiones, y se distingue de los espacios euclídeos con curvatura cero, que define la geometría
euclídea , y de la geometría elíptica , que tiene curvatura constante positiva.
Al embeberse en un espacio euclídeo (de mayor dimensión), todo punto de un espacio hiperbólico es
un punto de silla . Otra propiedad importante es la cantidad de espacio cubierto por la n-bola en el nespacio hiperbólico, que aumenta exponencialmente con respecto a la radio de la bola para radios
grandes, en lugar de polinómicamente .
Definición formal
El
n-espacio
hiperbólico,
denotado,
es
la variedad
riemanniana maximalmente
simétrica, simplemente conexa de dimensión n con curvatura seccional constante negativa. El
espacio hiperbólico es un espacio que presenta geometría hiperbólica . Es el análogo de la curvatura
negativa de la n-esfera . Aunque el espacio hiperbólico es difeomorfo a, su métrica de curvatura
negativa le da propiedades geométricas muy diferentes.
El 2-espacio hiperbólico, , se conoce también como plano hiperbólico .
Modelos del espacio hiperbólico
El espacio hiperbólico, desarrollado independientemente por Nikolái Lobachevski y János Bolyai ,
es un espacio geométrico análogo al espacio euclídeo , pero tal que el quinto postulado de Euclides no
se cumple. En su lugar, se establece el siguiente postulado alternativo (en dos dimensiones):
Dada cualquier recta y cualquier punto que no esté en , existen al menos dos rectas diferentes
que pasan por y no intersecan .LPLPL
Existe un teorema que dice que hay infinitas rectas de este tipo que pasan por . Este axioma no
caracteriza de forma única el plano hiperbólico salvo isometría , sino que es necesario añadir una
constante adicional, la curvatura , que debe especificarse. Sin embargo, lo caracteriza unívocamente
salvo homotecia , es decir, salvo biyecciones que solo que solo cambian la noción de distancia por
una constante general. Eligiendo una constante adecuada, se puede asumir sin pérdida de generalidad
que . PK<OK=-1
Se puede construir modelos de espacios hiperbólicos que pueden embeberse en un espacio
euclídeo . En particular, la existencia de estos modelos prueba que el quinto postulado
es independiente de los otros axiomas de la geometría euclídea .
Existen varios importantes del espacio hiperbólico: el modelo de Klein, el modelo del hiperboloide,
el modelo de la bola de Poincaré y el modelo del semiespacio de Poincaré. Todos ellos modelan la
misma geometría en el sentido de que pueden relacionarse entre sí por transformaciones que
conservan todas las propiedades geométricas del espacio, incluida la isometría (aunque no con
respecto a la métrica del embebimiento euclídeo).
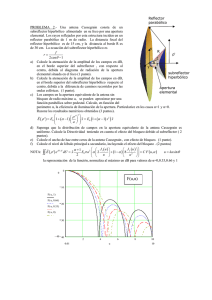
El modelo del hiperboloide caracteriza el espacio hiperbólico como un hiperboloide en . El
hiperboloide es el lugar geométrico de puntos cuyas coordenadas satisfacen
ℝ𝑛+1 = {𝑥0, … , 𝑥𝑛, |𝑥𝑖 ∈ ℝ, 𝑖 = 0,1, … , 𝑛}ℍ𝑛
𝑥02 − 𝑥12 − ⋯ − 𝑥𝑛2 = 1, 𝑥0 > 0.
En este modelo, las geodésicas serán las curvas formadas por la intersección de con un plano que pase
por el origen en . ℍ𝑛 ℝ𝑛+1
El modelo del hiperboloide está íntimamente relacionado con la geometría del espacio de
Minkowski . La forma cuadrática
𝑄(𝑥) = 𝑥02 − 𝑥12 − 𝑥22 … − 𝑥𝑛2 ,
que define el hiperboloide, se polariza para obtener la forma bilineal
𝐵(𝑥, 𝑦) =
𝑄(𝑥+𝑦)−𝑄(𝑥)−𝑄(𝑦)
2
= 𝑥0 𝑦0 − 𝑥1 𝑦1 − ⋯ − 𝑥𝑛 𝑦𝑛 ,
El espacio , equipado con la forma bilineal , es un espacio de Minkowski de
dimensión,. ℝ𝑛+1 𝐵(𝑛 + 1)ℝ𝑛,1
Se puede asociar una distancia en el modelo del hiperboloide,
entre dos puntos e en como 𝑥𝑦ℍ𝑛
[1]
definiendo la distancia
Donde 𝑑(𝑥, 𝑦) = 𝑎𝑟𝑐𝑜𝑠ℎ𝐵(𝑥, 𝑦).
Esta función satisface los axiomas de un espacio métrico . Se preserva bajo
la acción del grupo de Lorentz en . Así, el grupo de Lorentz actúa como un grupo de
transformaciones que conserva las isometrías en . ℝ𝑛,1 ℍ𝑛
El modelo de Klein
Un modelo alternativo de la geometría hiperbólica se define en un cierto dominio
del espacio proyectivo . La forma cuadrática define un subconjunto dado por el lugar
geométrico de los puntos para los que en las coordenadas homogéneas . El dominio es el
modelo de Klein del espacio hiperbólico. 𝑄𝑈 𝑛 ⊂ ℝℙ𝑛 𝑄 (𝑥) > 0𝑥𝑈 𝑛
Las geodésicas de este modelo son los segmentos de rectos abiertos del espacio
proyectivo ambiente que yacen en . La distancia entre dos puntos y viene
definida por𝑈 𝑛 𝑥𝑦𝑈 𝑛
𝑑(𝑥, 𝑦) = 𝑎𝑟𝑐𝑜𝑠ℎ (
𝐵(𝑥, 𝑦)
√𝑄(𝑥)𝑄(𝑦)
)
Esta distancia está bien definida en el espacio proyectivo, ya que el argumento del coseno
hiperbólico inverso es homogéneo de grado 0.
Este modelo se relaciona con el modelo del hiperboloide como sigue. Cada punto se
corresponde con una recta que pasa por el origen en , por la definición de espacio
proyectivo. Esta recta interseca al hiperboloide en un único punto. Análogamente, a
través de cualquier punto de pasa una única recta que pase además por el origen (que es
un
punto
en
el
espacio
proyectivo). Esta
correspondencia
define
una biyección entre y . Es además una isometría, ya que al evaluar a lo largo de se
reproduce la definición de distancia dada para el modelo del hiperboloide.
𝑥 ∈ 𝑈 𝑛 𝐿𝑥 ℝ𝑛+1 ℍ𝑛 ℍ𝑛 𝑈𝑛 ℍ𝑛 𝑑(𝑥, 𝑦)𝑄(𝑥) = 𝑄(𝑦) = 1
El modelo de la bola de Poincaré
Dos modelos íntimamente relacionados de la geometría hiperbólica son los modelos de
la bola de Poincaré y del semiespacio de Poincaré.
El modelo de la bola proviene de una proyección estereográfica del hiperboloide en
el hiperplano . De forma más detallada, sea el punto en con coordenadas , el polo sur de
la proyección estereográfica. Para cada punto en el hiperboloide , sea el único punto de
intersección de la recta con el plano .
ℝ𝑛+1 {𝑥0 = 0}𝑆ℝ𝑛,1 (−1,0,0, … , 0)
𝑃ℝ𝑛 𝑃 ∗ 𝑆𝑃{𝑥0 = 0}
Esto establece una biyección de la bola unidad ℍ𝑛
𝐵𝑛 = {(𝑥1 , … , 𝑥𝑛 )|𝑥12 + 𝑥𝑛2 < 1}
En plano {𝑥0 = 0}
Las geodésicas en este modelo son semicírculos perpendiculares a la esfera frontera
de . Las isometrías de la bola están por la inversión esférica de hiperesferas
perpendiculares a la frontera. 𝐵𝑛
El modelo del semiespacio de Poincaré
El modelo del semiespacio resulta de aplicar inversión en una circunferencia con centro
un punto frontera en la bola de Poincaré y radio dos veces el radio.
Esto envía circunferencias en rectas y es además una transformación conforme . En
consecuencia, las geodésicas del modelo del semiespacio son rectas y circunferencias
perpendiculares al hiperplano frontera. 𝐵𝑛
Variedades hiperbólicas
Toda variedad completa , conexa y simplemente conexa de curvatura negativa
constante es isométrica al espacio hiperbólico real . En consecuencia, el recubridor
universal de cualquier variedad cerrada de curvatura constante negativa , esto es, una
variedad hiperbólica, es . Así, esta puede escribirse como donde es un grupo
discreto libre de torsión de isometrías en . Esto es, es un retículo en .
−1ℍ𝑛 𝑀 − 1ℍ𝑛 𝑀ℍ𝑛 /ΓΓℍ𝑛 Γ𝑆𝑂+ (𝑛, 1)
Superficies de Riemann
Las superficies hiperbólicas de dimensión 2 también pueden entenderse según el lenguaje
de superficies de Riemann . De acuerdo al teorema de uniformización, toda la superficie
de Riemann es o elíptica, o parabólica o hiperbólica. La mayoría de las superficies
hiperbólicas tienen un grupo fundamental no trivial ; los grupos que surgen de esta forma
se conocen como grupos fuchsianos. El espacio cociente del semiplano
superior módulo el grupo fundamental se conoce como modelo fuchsiano de la superficie
hiperbólica. El semiplano de Poincaré es también hiperbólico, pero es simplemente
conexo y no compacto . Es el recubridor universal
𝜋𝑖 = Γℍ2 /Γ de las otras superficies hiperbólicas.
La construcción análoga para las superficies hiperbólicas tridimensionales es el modelo
kleiniano.
https://www.wikiwand.com/es/Espacio_hiperb%C3%B3lico#/Modelos_del_espacio_hiperb%C3%B
3lico