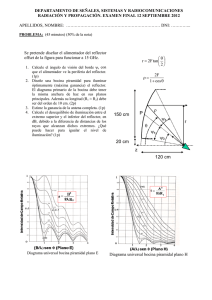
Solución Problema 2

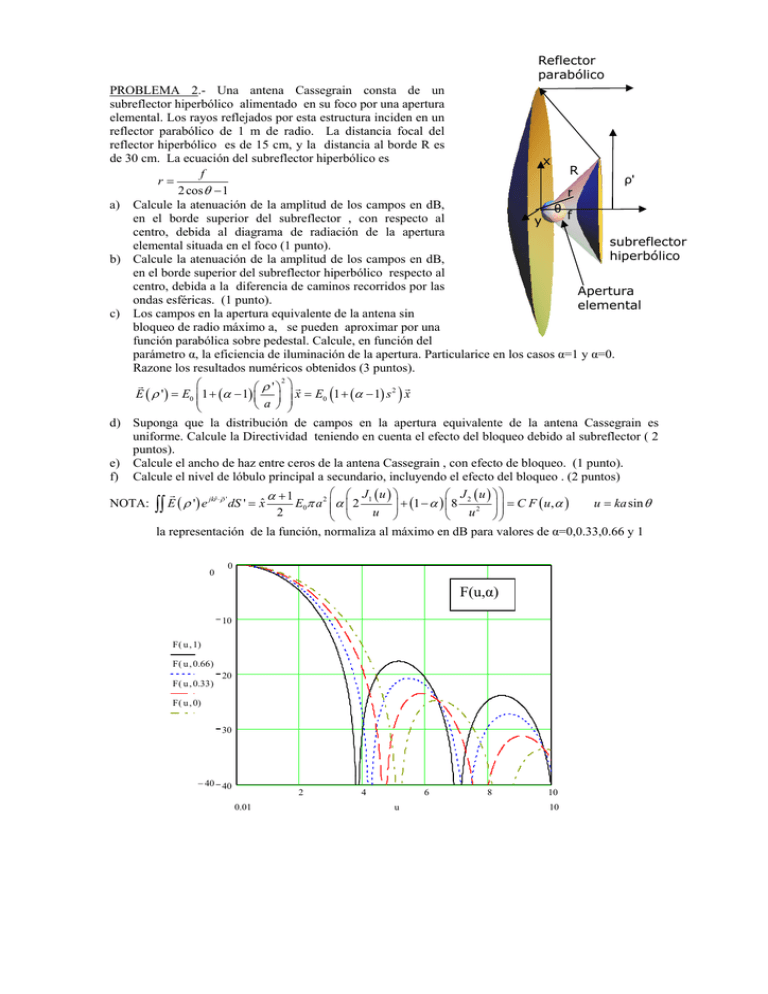
Reflector
parabólico
PROBLEMA 2.- Una antena Cassegrain consta de un
subreflector hiperbólico alimentado en su foco por una apertura
elemental. Los rayos reflejados por esta estructura inciden en un
reflector parabólico de 1 m de radio. La distancia focal del
reflector hiperbólico es de 15 cm, y la distancia al borde R es
de 30 cm. La ecuación del subreflector hiperbólico es
x
R
f
ρ'
r=
2 cos θ − 1
r
a) Calcule la atenuación de la amplitud de los campos en dB,
θ
f
en el borde superior del subreflector , con respecto al
y
centro, debida al diagrama de radiación de la apertura
subreflector
elemental situada en el foco (1 punto).
hiperbólico
b) Calcule la atenuación de la amplitud de los campos en dB,
en el borde superior del subreflector hiperbólico respecto al
centro, debida a la diferencia de caminos recorridos por las
Apertura
ondas esféricas. (1 punto).
elemental
c) Los campos en la apertura equivalente de la antena sin
bloqueo de radio máximo a, se pueden aproximar por una
función parabólica sobre pedestal. Calcule, en función del
parámetro α, la eficiencia de iluminación de la apertura. Particularice en los casos α=1 y α=0.
Razone los resultados numéricos obtenidos (3 puntos).
2
G

G
 ρ '  G
E ( ρ ' ) = E0  1 + (α − 1)    x = E0 (1 + (α − 1) s 2 ) x


 a  

d) Suponga que la distribución de campos en la apertura equivalente de la antena Cassegrain es
uniforme. Calcule la Directividad teniendo en cuenta el efecto del bloqueo debido al subreflector ( 2
puntos).
e) Calcule el ancho de haz entre ceros de la antena Cassegrain , con efecto de bloqueo. (1 punto).
f) Calcule el nivel de lóbulo principal a secundario, incluyendo el efecto del bloqueo . (2 puntos)
G
G
  J (u ) 
 J 2 (u )  
α +1
E0π a 2  α  2 1
u = ka sin θ
NOTA: ∫∫ E ( ρ ' ) e jkrˆ⋅ ρ ' dS ' = xˆ
 + (1 − α )  8 2   = C F ( u, α )

2
u 
 u 
 
la representación de la función, normaliza al máximo en dB para valores de α=0,0.33,0.66 y 1
0
0
F(u,α)
10
F ( u , 1)
F ( u , 0.66 )
F ( u , 0.33 )
20
F ( u , 0)
30
− 40 40
2
0.01
4
6
u
8
10
10
Solución
a) Atenuación debida al diagrama de la antena situada en el foco
El ángulo máximo se puede calcular a partir de la ecuación del reflector
hiperbólico
f
2 cos θ − 1
( n − 1) f = 1
2 cos θ − 1 =
R
2
r=
cosθ =
3
4
θ = 0.723rad = 41.41º
Por lo tanto, para la apertura elemental
 D (θ ', φ ' ) 
 4 θ 
 = 10 log  cos    = −1.16dB
D0
 2 



τ d = 10 log 
b) Atenuación debida a la diferencia de caminos
f=15 cm
r=R=30 cm
La atenuación será proporcional a
 f
 = −6dB
R
τ c = 20 log 
c) Cálculo de la eficiencia de iluminación
Los campos en la apertura son
2
G

G
 ρ ' 
E ( ρ ') = E0  1 + (α − 1)    = E0 (1 + (α − 1) s 2 ) x

 a  

El problema planteado tiene simetría de revolución. La eficiencia de
iluminación de una apertura circular es
2


 ∫∫ Ea ( x ', y ') ρ d ρ dφ ' 
1

ηil = 2  s '
2
πa
∫∫ Ea ( x ', y ') ρ d ρ dφ '
s'
2
2
2
a 

1

 ρ ' 
2
 ∫ E0 1 + (α − 1)    ρ ' d ρ ' 
E (1 + (α − 1) s ) sds 


4 ∫ 0
 a  
a
2π  0 
2
π
 =
0

ηil = 2
2
2
2 1
2
2
a
a
πa a 
π
 ρ ' 
E0 (1 + (α − 1) s 2 ) sds
∫
+
−
E
d
1
α
1
ρ
'
ρ
'
(
)




0
∫0 
0
 a  

2
2
1

2
α
1
+


s
sds
1
α
1
+
−
) ) 
∫( (


0

 =2  4 
ηil = 2 1
2
α 2 +α +1
2
s
sds
+
−
1
α
1
∫0 ( ( ) )
6
Para α=1 la distribución es uniforme, la eficiencia que se obtiene es 1.
Para α=0 la distribución es parabólica, la eficiencia es 0.75
d) Cálculo de la Directividad de la apertura bloqueada.
El radio del reflector hiperbólico es
a = R sin θ
a= 20.88 cm
La eficiencia de iluminación es 1.
El área efectiva es
2
D
Aef = π   − π a 2 = π (1 − 0.20882 ) = 3, 005m 2
2
La directividad es
4π
D = 2 Aef
D=46.228 dB
λ
e) Cálculo del ancho de haz de la apertura bloqueada.
Para una apertura circular uniforme de radio a el coeficiente α valdrá 1. El
diagrama de radiación será proporcional a la función
G
G
 J (u )
jkrˆ⋅ ρ '
ˆ 0π a 2  2 1
E
∫∫ ( ρ ') e dS ' = xE
u


 = C F ( u,1)

u = ka sin θ
Para el caso particular de una apertura bloqueada el diagrama será proporcional
a la función
G
  D  2  J1 ( u1 ) 
G
J1 ( u2 )
jkrˆ⋅ ρ '
2
ˆ
=
−
E
e
dS
xE
a
ρ
π
π
'
'
2
2
(
)




hip
0


∫∫
 2
u1 
u2




 

la relación entre los parámetros u1 y u2 es la relación entre las dimensiones del
reflector parabólico y el subreflector hiperbólico. La representación gráfica de
las dos funciones normalizadas es
0
0
10
F ( u , 1)
 u , 1
 4.789 
F
20
30
− 40 40
2
4
0.01
6
8
10
u
10
La relación entre las amplitudes de las dos funciones es:




2
πa 

= −27.2dB
20 log
  D 2 
π   
 2 
0
0
10
F ( u , 1)
   u , 1 −27.2 
  F
   4.789 

20
30
− 40 40
2
0.01
4
6
u
8
10
10
Para que se produzca un nulo es necesario que las dos funciones tomen el mismo
valor. Esto sucede aproximadamente para u=3.6
D
sin θ
2
θ = 0.9740
u=k
sin θ =
3.6λ
= 0.017
2π
El ancho de haz entre ceros será el doble ∆θ = 1.950
f) Cálculo de la relación de lóbulo principal a secundario de la apertura
bloqueada.
A partir de las gráficas se observa que la relación de lóbulo principal a
secundario de la apertura sin bloquear es -17.6 dB
Cuando se produce el efecto de bloqueo, hay una reducción del lóbulo principal,
proporcional al la disminución del área efectiva, y un aumento del lóbulo
secundario aproximadamente igual.
El lóbulo principal disminuye un factor proporcional a la eficiencia de bloqueo.
π (12 − 0.20882 )
π 12
= 0.956
El lóbulo secundario aumentará proporcionalmente a
π (12 − 0.2088210−17.6 / 20 )
π 12
=
El nuevo NLPS es -15.4 dB
0
0
10
F ( u , 1)
   u , 1 −27.2 
  F
   4.789 

20
G ( u)
30
− 40 40
2
0.01
4
6
u
8
10
10