Lamina 24 Ecuación de segundo grado y función cuadrática unlocked

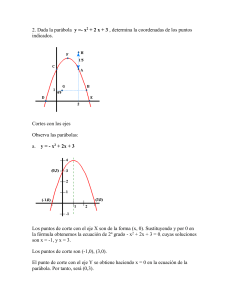
Lámina coleccionable
Matemática
y
“Ecuación de segundo grado
función cuadrática”
Síntesis de contenidos
1
• Función cuadrática
Son aquellas funciones de la forma f(x) = ax2 + bx + c, con a, b y c números reales y a ≠ 0. Su
dominio son los números reales y su recorrido está determinado por su vértice.
• Representación
gráfica de la función
Su representación gráfica corresponde a una parábola, tal que:
• La orientación de la concavidad depende del coeficiente a. Si:
a > 0 ⇒ concavidad hacia arriba (tiene un valor mínimo).
a < 0 ⇒ concavidad hacia abajo (tiene un valor máximo).
• La parábola intersecta al eje Y en el punto (0, c).
• El vértice de la parábola corresponde al punto más alto (si a<0) o más bajo (si a>0) de la parábola.
Está dado por:
(
– b 4ac – b2
(h,k) = 2a , 4a
)
h: Eje de simetría, es decir, la recta x = h divide a la parábola en dos partes idénticas.
k: Máximo o mínimo valor que toma la función. Determina el recorrido de la función.
• El discriminante de la función, Δ = b2 – 4ac, determina la(s) intersección(es) con el eje X (o soluciones
de la ecuación de segundo grado) Si:
∆ > 0 ⇒ La parábola intersecta al eje X en dos puntos distintos (la ecuación tiene dos soluciones
reales y distintas).
∆ = 0 ⇒ La parábola intersecta al eje X en un punto (la ecuación tiene dos soluciones reales e
iguales).
∆ < 0 ⇒ La parábola no intersecta al eje X (la ecuación tiene dos soluciones complejas conjugadas).
• Intersección(es) con
el eje X
• Ecuación de segundo
grado
Para determinar la(s) intersección(es) de la gráfica de una función cuadrática con el eje X, f(x) debe ser
igual a 0, es decir:
ax2 + bx + c = 0
Son aquellas ecuaciones donde la incógnita tiene como mayor exponente el dos (grado 2).
En una ecuación de segundo grado:
• Las soluciones se pueden determinar factorizando la expresión algebraica e igualando cada factor a cero.
Ej: x2 + 3x – 10 = 0 ⇒ (x + 5)(x – 2) = 0 ⇒ x1 = – 5, x2 = 2
• Se pueden resolver mediante la fórmula: x =
Ej: x2 + 3x – 10 = 0 ⇒
• Composición de
ecuaciones a partir
de las raíces
– b ± �Δ
2a
– 3 ± �32 – 4 • 1 • (– 10)
–3±7
=
⇒ x1 = – 5, x2 = 2
2•1
2
Si se conocen las raíces de una ecuación cuadrática, se puede determinar la ecuación cuadrática mediante
las fórmulas:
x1 + x2 =
–b
c
⇒ (x – x1)( x – x2) = 0
, ⇒ x1 • x2 =
a
a
Ejercicios propuestos
1
2
Las raíces (o soluciones) de la ecuación
x(x + 13) = 30 son
4
El vértice de la parábola de función
f(x) = 3x2 – 6x + 9 es
A)
30 y
–1
A)
(2, 9)
B)
15 y
–2
B)
(1, 6)
C)
10 y
–3
C)
(– 1, 18)
D)
5 y
–6
D)
(– 2, 33)
E)
2 y – 15
E)
ninguno de los puntos anteriores.
¿Cuál es la ecuación de segundo grado cuyas
raíces (o soluciones) son 5 y – 11?
A)
x2 + 6x – 55 = 0
B)
x2 + 6x + 55 = 0
5
¿Cuál(es) de las siguientes gráficas NO podría(n)
corresponder a f(x) = ax2 + bx + c, con a > 0
y c > 0?
I)
y
2
C)
x – 6x + 55 = 0
D)
x2 – 6x – 55 = 0
E)
x2 – 16x – 55 = 0
x
II)
y
x
3
2
Un cuadro rectangular de 30 m de superficie
tiene 1 metro más de frente que de fondo. Si x
es la medida del fondo, ¿cuál de las siguientes
ecuaciones permite calcular las dimensiones del
cuadro?
A)
x(x – 1) – 30 = 0
B)
x(x + 1) – 30 = 0
C)
x(x – 1) + 30 = 0
D)
x2 – 28 = 0
E)
2x – 30 = 0
2
III)
y
x
A)
B)
C)
D)
E)
Solo I
Solo III
Solo I y II
Solo I y III
Solo II y III