Encontrar la ecuación de una parábola dado el vértice

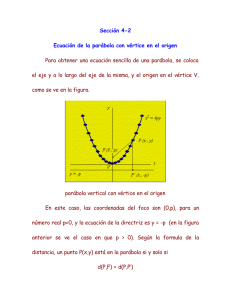
Encuentra la ecuación de la parábola cuyo vertice está en el punto (3; 2) y cuyo foco está en el punto (7; 2).
Solución:
Para encontrar esta ecuación debemos utilizar el siguiente teorema:
La ecuación de la parábola con vertice en el punto (h; k) y foco en el punto (h + a; k) es
(y
2
k) = 4a (x
h)
En nuestro caso es fácil ver que
h = 3;
k = 2; y a = 5
así que la ecuación será
(y
2
2) = 4 (5) (x
3)
Realizando las operaciones indicadas,
y2
4y + 4 = 20x
60
Que se escribe más armoniosamente como,
y2
4y
20x + 64 = 0
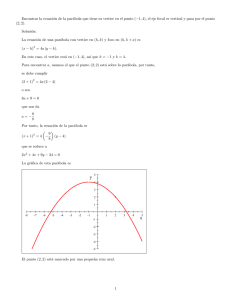
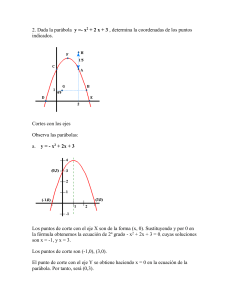
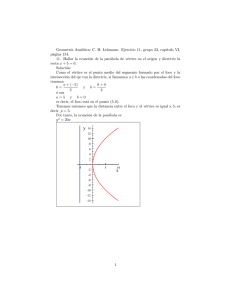
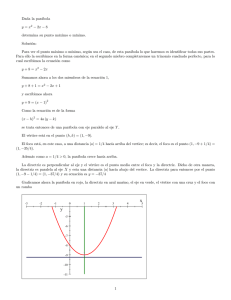
La grá…ca de la parábola es:
y
20
10
0
5
10
15
20
25
x
-10
-20
1