Determinar el punto máximo o mínimo de una parábola

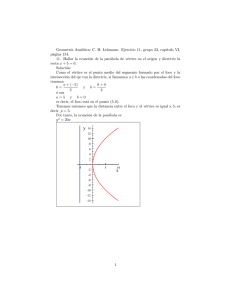
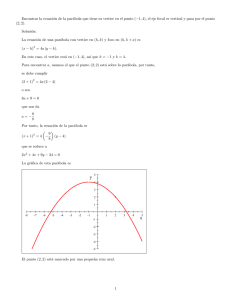
Dada la parábola
y = x2
2x
8
determina su punto máximo o mínimo.
Solución:
Para ver el punto máximo o mínimo, según sea el caso, de esta parábola lo que haremos es identi…car todas sus partes.
Para ello la escribimos en la forma canónica; en el segundo miebro completaremos un trinomio cuadrado perfecto, para lo
cual escribimos la ecuación como
y + 8 = x2
2x
Sumamos ahora a los dos miembros de la ecuación 1,
y + 8 + 1 = x2
2x + 1
y escribimos ahora
2
y + 9 = (x
1)
Como la ecuación es de la forma
(x
2
h) = 4a (y
k)
se trata entonces de una parábola con eje paralelo al eje Y .
El vértice está en el punto (h; k) = (1; 9).
El foco está, en este caso, a una distancia jaj = 1=4 hacía arriba del vertice; es decir, el foco es el punto (1; 9 + 1=4) =
(1; 35=4).
Además como a = 1=4 > 0, la parábola crece hacía arriba.
La directriz es perpendicular al eje y el vértice es el punto medio entre el foco y la directriz. Dicho de otra manera,
la directriz es paralela al eje X y esta una distancia jaj hacía abajo del vertice. La directriz para entonces por el punto
(1; 9 1=4) = (1; 37=4) y su ecuación es y = 37=4
Gra…camos ahora la parábola en rojo, la directriz en azul marino, el eje en verde, el vértice con una cruz y el foco con
un rombo
-3
-2
-1
0
1
2
3
4
y
-5
-6
-7
-8
-9
-10
-11
1
x
5
Tenemos entonces que esta parábola presenta un mínimo que está dado por su vertice; es decir, el valor mínimo de la
parábola es el punto (1; 9).
2