Vértice de una parábola
El teorema que sigue es una fórmula sencilla para localizar él
vértice de una parábola.
El vértice de la parábola y = ax2 + bx + c tiene como
coordenadas:
−b
b2
, c −
4a
2a
Demostración
Se inicia expresando y = ax2 + bx + c en la forma
b
y = a x 2 + x + c
a
2
1 b
A continuación se completa el cuadrado sumando
a la
2 a
expresión entre paréntesis:
2 b
b2
b2
y = a x + x + 2 + c −
a
4a
4a
Nótese que si b2/(4a2) se suma al interior del paréntesis,
entonces, debido al factor a que se halla fuera de él, en realidad
se habrá sumado b2/(4a) a y. Entonces, debemos compensarlo
restando b2/(4a). La última ecuación se puede escribir en la
siguiente forma:
2
b
b2
y = a x + + c −
2a
4a
.
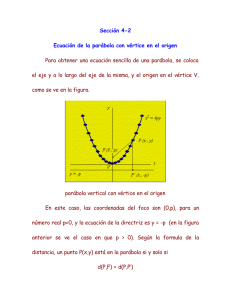
Es la ecuación de una parábola que tiene su vértice en (h, k).