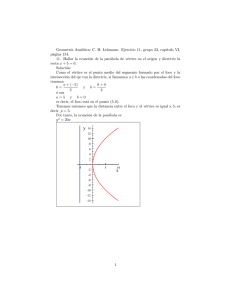
El beneficio marginal de cierta compañía es de 100 − 2𝑥, dólares por unidad cuando el nivel de producción es 𝑥 unidades. Si el beneficio marginal de la compañía es de $ 800cuando se producen 15 unidades ¿Cuál es el mayor beneficio para la compañía? Solución. Sea 𝐵 = 𝐵(𝑥) la función que define el beneficio (ingreso neto) de la compañía cuando el nivel de producción es de 𝑥 unidades. Aplicando propiedades de la integral indefinida o primitiva de una función, específicamente el Teorema fundamental del Cálculo, tenemos que, 𝐵(𝑥) = ∫ 𝐵 ′ (𝑥)𝑑𝑥 De este modo, 𝐵(𝑥) = ∫(100 − 2𝑥)𝑑𝑥 𝐵(𝑥) = ∫ 100𝑑𝑥 − ∫ 2𝑥𝑑𝑥 𝐵(𝑥) = 100𝑥 − 𝑥 2 + 𝐶 La condición dada significa que 𝐵 = 800 si 𝑥 = 15, es decir 𝐵(15) = 800, ésta última igualdad, nos permite calcular el valor de la constante 𝐶, 100(15) − (15)2 + 𝐶 = 800 1500 − 225 + 𝐶 = 800 1275 + 𝐶 = 800 𝐶 = 800 − 1275 = −475 𝐶 = −475 La función Beneficio es, 𝐵(𝑥) = 100𝑥 − 𝑥 2 − 475 Geométricamente, la gráfica de la función beneficio describe una parábola de ecuación de la forma 𝑦 = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐 donde 𝑎 = −1 < 0 indica que abre hacia abajo y el máximo valor de 𝑦, corresponde a la ordenada del vértice de dicha parábola. Aplicamos completación de cuadrados, 𝑦 = −𝑥 2 + 100𝑥 − 475 𝑦 = −(𝑥 2 − 100𝑥 + (50)2 ) − 475 + (50)2 𝑦 = −(𝑥 − 50)2 − 475 + 2500 𝑦 = −(𝑥 − 50)2 + 2025 𝑦 − 2025 = −(𝑥 − 50)2 (𝑥 − 50)2 = −(𝑦 − 2025) Hemos escrito la ecuación de la parábola en su forma canónica, (𝑥 − ℎ)2 = 4𝑝(𝑦 − 𝑘) Donde identificamos el vértice 𝑉(ℎ, 𝑘), la ordenada del vértice es 𝑘 = 2025 Se concluye que el máximo beneficio obtenido es de $ 2025. Gráfica de la función Beneficio.