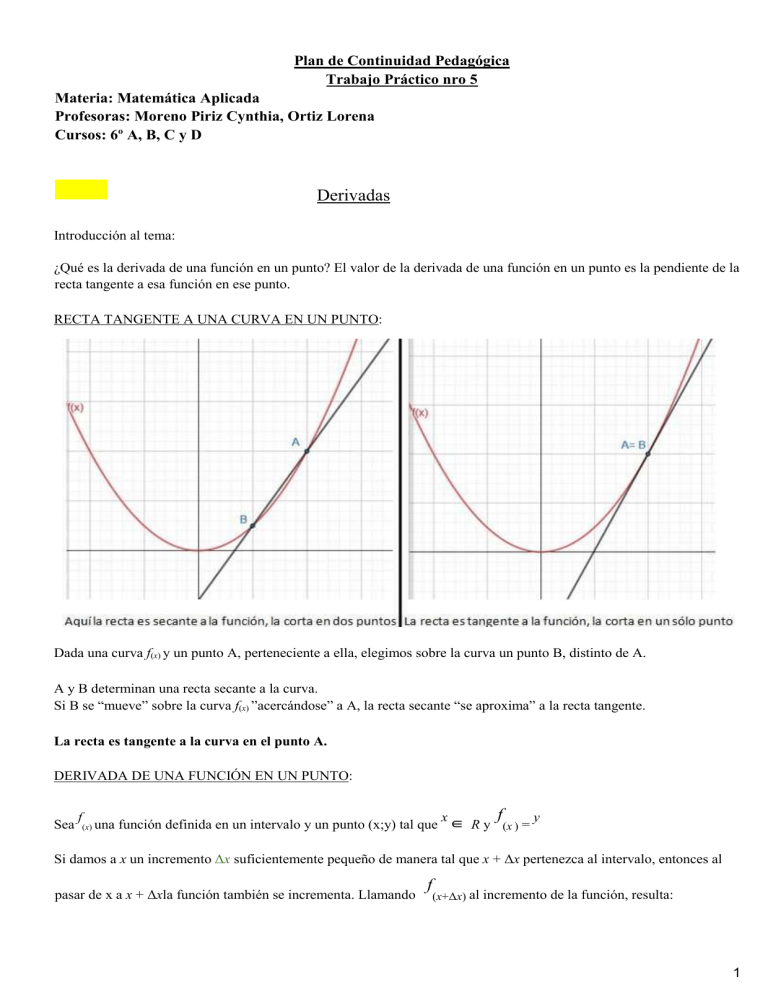
Plan de Continuidad Pedagógica Trabajo Práctico nro 5 Materia: Matemática Aplicada Profesoras: Moreno Piriz Cynthia, Ortiz Lorena Cursos: 6º A, B, C y D Derivadas Introducción al tema: ¿Qué es la derivada de una función en un punto? El valor de la derivada de una función en un punto es la pendiente de la recta tangente a esa función en ese punto. RECTA TANGENTE A UNA CURVA EN UN PUNTO: Dada una curva f(x) y un punto A, perteneciente a ella, elegimos sobre la curva un punto B, distinto de A. A y B determinan una recta secante a la curva. Si B se “mueve” sobre la curva f(x) ”acercándose” a A, la recta secante “se aproxima” a la recta tangente. La recta es tangente a la curva en el punto A. DERIVADA DE UNA FUNCIÓN EN UN PUNTO: Sea f (x) una f x y función definida en un intervalo y un punto (x;y) tal que ∈ R y (x ) = Si damos a x un incremento Δx suficientemente pequeño de manera tal que x + Δx pertenezca al intervalo, entonces al pasar de x a x + Δxla función también se incrementa. Llamando f (x+Δx) al incremento de la función, resulta: 1 f(x+Δx) , es f (x) con el agregado del incremento en el valor de la función (lo marcado con celeste en el gráfico) ( ) Como el incremento Δx se ha tomado suficientemente pequeño, el punto A de coordenadas x + Δx;f(x+Δx) , perteneciente a la gráfica de la función, resulta muy próxima a B y esta proximidad de A a B será mayor, cuanto menor sea Δx. Los dos puntos están en el mismo lugar cuando la distancia entre ellos tiende a cero. Luego, si Δx → 0, A se “moverá” sobre la curva hacia B y la secante determinada por dichos puntos tenderá a la recta tangente. Si observamos el eje x, cuando 2 Observemos que cuando la recta secante tiende a la recta tangente, αtiende a αt y por consiguiente la pendiente de la secante tiende a la pendiente de la recta tangente. Derivada por definición Hallar la derivada por definición de: Ejemplo 1: f(x) =2 x + 1 3 Como dijimos, la derivada es la pendiente de la recta tangente de una función en un punto, en este caso como derivamos una función lineal cuya pendiente es 2 en cualquiera de sus puntos era evidente que tenía que dar ese valor. Ejemplo 2: f(x) = x 2 - 4 Como la derivada por definición se calcula con: 4 se puede resolver con propiedad distributiva o binomio al cuadrado 2 * (x + Δx) = (x + Δx).( x + Δx ) = x2 + x. Δx + Δx . x + Δx2 = x2 + 2. x. Δx + Δx2 Ejemplo 3: f(x) = 3x 2 5 Ejemplo 4: f(x) = x2 + x EJERCICIOS 1) Hallar la derivada por definición de las siguientes funciones: a) f(x) = 3x − 5 b) f(x) = − 4.x + 2 c) f(x) = x2 + 1 d) f(x) = -x2 + 9 e) f(x) = 5.x2 f) f(x) = 3x2 + 4x 6 El procedimiento para calcular la derivada de una función aplicando siempre la definición, es poco práctico. Ya que es un procedimiento largo y para muchas funciones es complicado. En los ejemplos y actividades que dimos, trabajamos las más sencillas. Y gracias a la labor de los matemáticos podemos contar con reglas que nos permitan derivar directamente. Dichas reglas y derivadas surgen de aplicar la definición, pero se resumen en una tabla. Analicemos los ejemplos y después ustedes analicen los ejercicios para ver que sucede entre la función y su derivada. EJEMPLO 1: f (x) = 2x + 1 ⇒ f′ (x) = 2 + 0 EJEMPLO 2: f(x) = x2 − 4 ⇒ f′ (x) = 2x − 0 EJEMPLO 3: f(x) = 3x2 ⇒ f′ (x) = 6x EJEMPLO 4: f(x) = x2 + x ⇒ f′ (x) = 2x + 1 Si te afirmo que en los casos de funciones polinómicas con sumas y resta, se deriva por término: * El término independiente en el ejemplo 1 y 2: f(x) = 2x + 1 ⇒ f′ (x) = 2 + 0 f(x) = x2 - 4 ⇒ f′ (x) = 2x - 0 o sea, que la derivada de una constante (un número real) es siempre cero. * Los términos lineales: ax (considerando que a es un número), veamos el ejemplo 1 y 4: f(x) =2x+ 1 ⇒ f′ (x) =2+ 0 f(x) = x2 + x ⇒ f′ (x) = 2x +1 o sea,la derivada de ax será solo a * la derivada de: a x n (una polinómica, donde n es el exponente y a el coeficiente),veamos ejemplo 2, 3 y4: f(x) = x2 - 4 ⇒ f′ (x) = 2x - 0 , tenemos 2 x f(x) = 3x2 ⇒ f′ (x) = 6x, pensemos que 6x es 3.2x f(x) = x2 + x ⇒ f′ (x) = 2x + 1 o sea, la derivada de: a x n será a. n . x n−1 Es decir; que si hay un coeficiente (número) multiplicando a una función, éste queda solo se agrega; y se deriva la función que lo acompaña. Estas son dos de las regla de derivada más sencillas, a continuación les dejamos la tabla de derivada que usaremos de ahora en adelante para facilitar todo el desarrollo de la derivada por definición y podamos avanzar en los ejercicios de 7 derivada que es muy interesante y encontrarán importantes análisis con ella. Ejemplos de derivadas sencillas utilizando la tabla: miramos en la tabla la derivada de la función seno es coseno Ejemplo 1: f(x) = − sen x f′ (x) = − cos x Ejemplo 2: f(x) = 7x2 − 4x + 9 4.1.x1−1 + 0 derivamos cada uno de los términos teniendo en cuenta que f′ (x) = 7. 2x2−1 − si f(x) = xn ⇒ f′ (x) = n. xn−1 y que la derivada de una constante es cero f′ (x) = 14 x − 4 el término 4.1x1−1 = 4.x0 = 4 porque sabemos que x0 =1 Ejemplo 3:f(x) = log 2 x f′ (x) = 1 x. observamos en la tabla que la derivada de la función logarítmica es log2e f′ (x) = 1x . logae Ejemplo 4: f(x) = x5 − 3x4 + x derivamos cada uno de los términos teniendo en cuenta que f′ (x) = 5x5−1 − 3.4x4−1 + 1x1−1 si f(x) = xn ⇒ f′ (x) = n. xn−1 f′ (x) = 5x4 − 12 x3 + 1 8 9