Regresion y estadistica

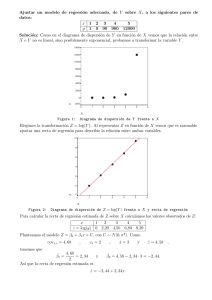
3. Regresión lineal
Curso 2011-2012
Estadística
Regresión simple
consumo y peso de automóviles
Peso
kg
Consumo
litros/100 km
1
981
878
708
1138
1064
655
1273
1485
1366
1351
1635
900
888
766
981
729
1034
1384
776
835
650
956
688
716
608
802
1578
688
1461
1556
11
12
8
11
13
6
14
17
18
18
20
10
7
9
13
7
12
17
12
10
9
12
8
7
7
11
18
7
17
15
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Regresión Lineal
25
Consumo (litros/100 Km)
Núm. Obs.
(i)
20
15
10
5
0
500
700
900
1100
1300
1500
1700
Peso (Kg)
2
Modelo
yi
1 xi
0
ui ,
ui
N (0,
2
)
yi
0
1
x
xi
2
,
,
: parámetros desconocid os
0
1
Regresión Lineal
3
Hipótesis del modelo
Linealidad
yi =
0+ 1xi
+ ui
Parámetros
Normalidad
yi|xi
N ( 0 + 1x i, 2)
Homocedasticidad
Var [yi|xi] =
2
0
1
2
Independencia
Cov [yi, yk] = 0
Regresión Lineal
4
Modelo
yi
1 xi
0
ui ,
ui
2
N (0,
)
yi : Variable dependiente
xi : Variable independiente
ui : Parte aleatoria
0
Regresión Lineal
5
Estimación
n
M(
0
,
1
( yi
)
x )2
0
1 i
i 1
n
dM
d 0
dM
d 0
( yi
0
x) 0
yi
1 i
n
0
xi
1
i 1
n
( yi
0
x ) xi
0
1 i
xi yi
xi
0
xi2
1
i 1
n
y
( yi
1x
0
n
y )( xi
x)
( xi
i 1
n
xi yi n
0
x
1
2
i
x n
x) 2
i 1
1
n
n
i 1
1
Regresión Lineal
cov( xi , yi )
;
var( xi )
0
y
1
x
6
Estimación: máxima verosimilitud
1
l ( 0 , 1, 2 )
2 2i 1
( yi
1xi )
0
2
i 1
1 n
2i 1
y
i 1
2
n
n
1
L( 0 , 1, 2 ) log l ( 0 , 1, 2 )
n
n
1 n
2
log( 2 )
log 2
( yi
0
1xi )
2
2
2
2 i 1
1 n
( yi
yi n 0
0
1xi ) 0
1 xi
2
dL
d 0
dL
d 0
n
n/2
exp
xi yi n
( yi
1xi ) xi
0
n
1x
0
0x
1
i 1
xi2 n
1
0
( yi
xi yi
y )( xi
n
x)
1
n
cov( xi , yi )
;
var( xi )
y
0
2
1 xi
xi
0
i 1
( xi
x)2
n
1x
Regresión Lineal
7
2
Estimación
L( 0 , 1, 2 )
dL
d
2
: máxima verosimilitud
n
n
log( 2 )
log 2
2
2
n 1
1 n
( yi
2
4
2
2 i 1
n
2
i 1
( yi
2 2i 1
( yi
1xi )
0
1xi )
0
n
1
2
0
2
x
)
1 i
0
2
n
ei
yi
0
1 xi
n
n
ei
0
s R2
i 1
n
ei xi
0
ei2
i 1
n 2
i 1
Regresión Lineal
8
Estimación
Máxima verosimilitud
Max
1
2
n/2
exp
n
1
2
n
2
( yi
x )2
0
1 i
i 1
Mínimos cuadrados
n
Mín
( yi
0
2
x
)
1 i
i 1
y
0
1
x
cov( xi , yi )
var( xi )
1
n
i 1
( xi
x )( yi y )
n
x )2
i 1 ( xi
Regresión Lineal
9
Recta de regresión
y
1x
0
y
Pendiente
1
0
y
1x
x
Regresión Lineal
10
Residuos
yi
1 xi
ei
Valor Previsto Residuo
0
Valor observado
ei
yi
yi
0
1 xi
xi
Regresión Lineal
11
Ejemplo: estimación
Peso
kg
Consumo
litros/100 km
Predicción
Residuos
1
981
878
708
1138
1064
655
1273
1485
1366
1351
1635
900
888
766
981
729
1034
1384
776
835
650
956
688
716
608
802
1578
688
1461
1556
11
12
8
11
13
6
14
17
18
18
20
10
7
9
13
7
12
17
12
10
9
12
8
7
7
11
18
7
17
15
11,44
10,23
8,23
13,28
12,41
7,61
14,86
17,35
15,95
15,78
19,11
10,49
10,35
8,91
11,44
8,48
12,06
16,16
9,03
9,72
7,55
11,14
8,00
8,33
7,06
9,34
18,44
8,00
17,07
18,18
-0,44
1,77
-0,23
-2,28
0,59
-1,61
-0,86
-0,35
2,05
2,22
0,89
-0,49
-3,35
0,09
1,56
-1,48
-0,06
0,84
2,97
0,28
1,45
0,86
0,00
-1,33
-0,06
1,66
-0,44
-1,00
-0,07
-3,18
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Regresión Lineal
25
Consumo (litros/100 Km)
Núm. Obs.
(i)
20
15
10
5
0
500
700
900
1100
1300
1500
1700
Peso (Kg)
yi
0.071 0.0117 xi
2
; sR
2.38
12
Propiedades de
1
1
ns x2
i 1
1
ns x2
wi
n
i 1
wi xi
1
ns x2
n
i 1
2
i
1
ns x2
w
n
i 1
xi
xi
x
xi
1
ns x2
x yi
w1 y1
1
ns x2
x xi
xi
y
n
xi
x y
w2 y2
wn yn
x
2
n
i 1
xi
1
ns x2
x xi
n
i 1
xi
x x
1
ns x2
n
i 1
xi
x
1
ns x2
Regresión Lineal
y,
xi x
ns x2
wi
i 1
0
2
n
i 1
x yi
i 1
i 1
xi
n
i 1
n
n
xi x
yi
ns x2
n
n
i 1
1
ns x2
0
cov( xi , yi )
s x2
1
13
son v.a. independientes
1
y1
1
y1
n
y
1
y2
n
1
yn
n
1
n
1
n
1
n
y2
aT Y
yn
y1
1
w1 y1 w2 y2
wn yn
w1
w2
wn
y2
wT Y
yn
2
cov( y ,
n
T
1
) a var(Y) w
Regresión Lineal
n
wi
0
i 1
14
2
1
Distribución de
yi
1
N(
w1 y1
2
x,
1 i
0
)
w2 y2
E[ 1 ] E[ w1 y1
wn yn
w2 y2
( wi )
1
Var[ 1 ] Var[ w1 y1
Comb. lineal de normales
wn yn ]
w1 E[ y1 ] w2 E[ y2 ]
0
1
( wi xi )
w2 y2
wn E[ yn ] ( E[ yi ]
1
wn yn ]
w12Var[ y1 ] w22Var[ y2 ]
n
x)
1 i
0
wn2 [ yn ] (Var[ yi ]
2
)
2
2
i
2
( w )
ns x2
i 1
2
N
1
1
,
ns x2
Regresión Lineal
15
Modelo en diferencias a la
media
yi
x
0
y
ei
1 i
0
1
x
yi
yi
y
1
( xi
x ) ei
yi
y
1
( xi
x)
Regresión Lineal
y
1
( xi
x ) ei
16
Distribución de
0
2
N(
y
0
1
x,
2
N(
1
y,
y
0
E[
1
x
1
n
)
,
)
ns x2
son independie ntes
1
Normal
] E[ y ] x E[ 1 ]
2
x2
var[ 0 ]
1 2
n
sx
0
2
0
0
x2
1 2
0,
n
sx
N
Regresión Lineal
17
2
R
yi
1xi
0
ui
ui
yi
0
1xi
ei
N (0, 2 )
n u2
i 1 i
2
n e2
i 1 i
2
2
n
n
ei2
i 1
2
Regresión Lineal
2
(n 2) s R
2
2
n 2
ei
0
ei xi
2
n 2
18
0
Contraste principal de regresión:
¿depende y de x?
H0 :
1
0
H1 :
1
0
yi
yi
yi
x
0
1 i
ui
yi
ui
0
xi
xi
H0 es falso
H0 es cierto
x e y están relacionados
x e y no están relacionados
Regresión Lineal
19
Contraste sobre la pendiente
H0 :
H1 :
1
0
1
0
1
yi
x
0
1 i
2
1
1
1
N ( 1,
Regresión Lineal
1
sR
nsx
;
t1
tn
)
1
N (0,1)
1
sR
ns x
ns x
t1
ns x2
2; / 2
tn
2
Se rechaza Ho
20
Contraste: ordenada en el origen
H0 :
H1 :
0
0
yi
0
0
x
0
1 i
2
x2
N ( 0 , (1 2 ))
n
sx
0
0
t0
t0
tn
2
sR
x
1 2
sx
n
;
Se rechaza Ho
2; / 2
Regresión Lineal
21
Descomposición de la
variabilidad en regresión
yi
0
1 i
x
yi
0
1 i
x
y
i
yi
( yi
n
( yi
y
i
(y
i
y)
y)
2
i 1
VT
ui
y
i
(y
i
y) ( y
i
n
( y y)
i
i 1
VE VNE
Regresión Lineal
ei
2
y
i
y ) (restando y )
i
y ) (elevando al cuadrado y sumando)
i
n
(y
i
i 1
y )2
i
22
Coeficiente de determinación R2
n
VE
( yi
y)2
i 1
n
( yi
VNE
i 1
n
VT
yi )
VT
R
2
R2
1
Mide el porcentaje de VT que
y)2
está explicado por el regresor
i 1
y
VE
VT
2
0
( yi
yi
VE VNE
1 ( xi
x) :
VE
2
1
n
( xi
x)2
2 2
1 ns x
i 1
Regresión Lineal
23
Coef. determinación
R2
R2
1
0.50
Regresión Lineal
R2
0.80
R2
0
24
Contraste F
H0 :
H1 :
VE
2
1
0
1
0
2
1
(Si H o es cierto)
n e2
i 1 i
2
VNE
2
1
yi
2
( n 2) s R
2
x
0
1 i
VE
VNE/(n-2 )
F
F
2
n 2
VE VNE
,
son independie ntes
2
F
VE
2
sR
F1,n
Se rechaza H0
2
Regresión Lineal
25
Regresión con R
ARCHIVO TEXTO: coches.txt
Regresión Lineal
2
26
Regresión con R: Estimación
Regresión Lineal
27
Gráfico en R
Regresión Lineal
28
Ejemplo regresión múltiple
Consumo =
0
+
CC +
1
2
Pot +
3 Peso
+
4
Acel + Error
Y
X1
X2
X3
X4
Consumo
l/100Km
15
16
24
9
11
17
...
Cilindrada
cc
4982
6391
5031
1491
2294
5752
...
Potencia
CV
150
190
200
70
72
153
...
Peso
kg
1144
1283
1458
651
802
1384
...
Aceleración
segundos
12
9
15
21
19
14
...
Var. dependientes
o respuesta
Var. Independientes
o regresores
Regresión Lineal
29
Modelo regresión múltiple
yi
0
1x1i
2 x2i
, k , 2 : parámetros desconocid os
Linealidad
E[yi] =
0+
Homocedasticidad
1x1i+
+
kxki
Normalidad
yi| x1 ,...,xk
Regresión Lineal
ui ,
N (0, 2 )
ui
0 , 1, 2 ,
k xki
Normal
Var [yi|x1 ,...,xk] =
2
Independencia
Cov [yi, yk] = 0
30
Notación matricial
y1
1
x11
x21
xk1
0
u1
y2
1
x12
x22
xk 2
1
u2
yn
1
x1n
x 2n
xkn
k
un
Y
X
U
2
N (0, I)
U
Regresión Lineal
31
Estimación mínimo-cuadrática
y1
1
x11
x21
xk1
0
e1
y2
1
x12
x22
xk 2
1
e2
yn
1
x1n
x 2n
xkn
k
en
Y
X
e
donde el vector e cumple
e
2
n
ei2
es mínimo
i 1
Regresión Lineal
32
Para que ||e||2 sea mínimo, e tiene que ser
perpendicular al espacio vectorial generado las
columnas de X
X
1
1
x11
x12
x21
x22
xk1
xk 2 , e
e1
e2
1
x1n
x2 n
xkn
en
X Te
0
n
1 i
n
1 i 1i
e 0
ex
0
n
1 i
e xki
0
Regresión Lineal
33
Mínimos cuadrados
Y
Solución MC
x1
Y
e
Y
Y
x1
x2
Y
T
X e 0
XT Y XT X
XT Y XT X
Regresión Lineal
X
x2
X Te
( X T X) 1 X T Y
34
Matriz de proyección V
Y
e
(I
V)Y
x1
Y
Val. Prev istos
Y X
Y X(X T X) 1 X T Y
Y VY
VY
1
Residuos
e Y X
Y VY
(I V)Y
X(XT X) 1 XT
V
Simétrica V=VT
Idempotente VV=V
Regresión Lineal
35
Distribución de probabilidad
de
Y
N ( X , 2I)
(X T X) 1 X T Y
CY (siendo C (X T X) 1 X T )
Normal
E[ ] CE[ Y ] CX
(X T X) 1 X T X
Var[ ] Var[CY ] CVar[Y ]CT
((X T X) 1 X T )( 2I )((X T X) 1 X T )T
Regresión Lineal
2
(X T X) 1 X T X(X T X) 1
2
(X T X) 1
36
Distribución de probabilidad
de
N ( , 2 (X T X) 1 )
N ( i , 2 qii )
i
0
0
1
1
Q
( X T X)
k
k
1
q00
q10
q01
q11
q0 k
q1k
qk 0
qk1
qkk
dim(Q)
(k 1) (k 1)
Regresión Lineal
37
Residuos
Y
X
e
Observados Previstos Residuos
y1
1
x11
x21
xk1
0
e1
y2
1
x12
x22
xk 2
1
e2
yn
1
x1n
x 2n
xkn
k
en
ei
yi
Regresión Lineal
( 0
1x1i
k xki )
38
Varianza Residual
n 2
i 1 ei
2
e Te
2
E[
E[
n e2
i 1 i ]
2
2
n k 1
n k 1
n e2
i 1 i ]
n e2
i 1 i
2
sR
n k 1
2
(n k 1) s R
2
2
2
n k 1
n k 1
Regresión Lineal
39
Contraste individual
yi
1x1i
0
k xki
i
i
i
ti
i
s R qii
Regresión Lineal
H0 : i
H1 : i
ui
1
1
s R qii
;
ti
0
0
N ( i , 2 qii )
N (0,1)
qii
i
t n k 1; / 2
tn k 1
Se rechaza Ho
40
Descomposición de la
variabilidad en regresión
yi
( yi
n (y
i 1 i
1x1i
0
yi
yi
y)
( yi
k xki
ei
(Restando y )
ei
y ) ei
y)2
n (y
i 1 i
y)2
VT
VE VNE
n e2
i 1 i
Regresión Lineal
41
Modelo en diferencias a la
media
yi
0
y
0
yi
0
yi
y
1x1i
k xki
1 x1
n
x1i
1
k
i 1
n
xki
i 1
ei
i 1
0
k xki
x1 )
k ( xki
x k1 x k
x k 2 xk
1
xkn
k
y
x11 x1
y2
y
x12
x1
x21 x2
x22 x2
yn
y
x1n
x1
x2 n
Regresión Lineal
n 0
i 1
y1
Y Y
n
yi
k xk
1x1i
1 ( x1i
n
ei
~
Xb
xk )
x2
Y Y
xk
2
~
Xb e
42
Modelo en diferencias a la
media
~ ~
Y Xb U
y1 y
~
Y
~
X
b
y2
y
yn
y
y
, Y
y
1
2
, b
y
1
, b
k
k
x11 x1
x21 x2
x12
x1
x22
x2
xk1 xk
xk 2 xk
x1n
x1
x2 n
x2
xkn
~T ~ 1 ~T ~
(X X) X Y
2
xk
~T ~ 1
2
N (b, (X X) )
b
Regresión Lineal
43
Contraste general de regresión.
yi
0
1x1i
k xki
ui
H0 : 1
2
k 0
H1 : algunoes distintode 0
VE
2
k
2
VNE
(Si Ho es cierto)
2
(n k 1) s R
2
2
2
n k 1
VE VNE
,
son independientes
2
2
Regresión Lineal
F
F
VE / k
VNE/(n-k 1 )
F
Fk ,n
k 1
Se rechaza H0
44
Coeficiente de determinación R2
n
VE
( yi
y)2
i 1
n
( yi
VNE
i 1
n
VT
yi )
( yi
R
2
VE
VT
2
R2
1
Mideel porcentajede VT que
y)2
está explicadopor los regresores
i 1
VE
VE VNE
0
( yi
n
VT
~ ~
(Y Y)T (Y Y) bT ( XT X)b
y)2
~ ~
bT ( XT Y)
i 1
Regresión Lineal
45
Coef. determinación corregido R
R2
VE
VT
VT VNE
VT
2
(n k 1) s R
1
(n 1) s 2y
VNE
1
VT
R2
Regresión Lineal
1
2
sR
s 2y
n
( yi
s 2y
y)2
i 1
n 1
VNE /(n k 1)
1
VT /(n 1)
46
2
Regresión con R
Interpretación (inicial)
Contraste F=438 (p-valor=0.0000)
Alguno de
los regresores influye significativamente en el
consumo.
Contrastes individuales:
La potencia y el peso influyen significativamente (pvalor=0.0000)
Para =0.05, la cilindrada y la aceleración también
tienen efecto significativo (p-valor < 0.05)
El efecto de cualquier regresor
aumentar cualquiera de ellos aumenta la variable
respuesta: consumo.
Los regresores explican el 82 % de la variabilidad
del consumo (R2 = 0.8197)
Regresión Lineal
48
Multicolinealidad
Cuando la correlación entre los
regresores es alta.
Presenta graves inconvenientes:
Empeora las estimaciones de los efectos de
cada variable i: aumenta la varianza de las
estimaciones y la dependencia de los
estimadores)
Dificulta la interpretación de los parámetros
del modelo estimado (ver el caso de la
aceleración en el ejemplo).
Regresión Lineal
49
Identificación de la multicolinealidad:
Matriz de correlación de los regresores.
Regresión Lineal
50
24
24
20
20
consumo
consumo
Gráficos consumo - xi
16
12
8
4
16
12
8
4
0
500
0
1000
1500
2000
0
40
120
160
200
240
23
26
potencia
24
24
20
20
consumo
consumo
peso
80
16
12
8
4
16
12
8
4
0
0
0
2
4
cilindrada
6
8
(X 1000)
8
11
14
17
20
aceleracion
Regresión Lineal
51
Consumo y aceleración
Regresión Lineal
52
Multicolinealidad: efecto en la
varianza de los estimadores
yi
var
1
~T X
~ 1 2
X
~T X
~
X
1x1i
0
nS XX
2 x2i ui
S XX
2
s12
s12
s12
r12 s1s2
s12
s22
r12 s1s2
s22
1
s12 (1
2
1
| S XX | s12 s22 (1 r12
) S XX
r12
2
r12
)
2
s1 s2 (1 r12
)
1
r12
2
s1 s2 (1 r12
)
2
s22 (1 r12
)
2
var
1
2
r12
2
ns12 (1 r122 )
r12 2
ns1 s2 (1 r122 )
ns1 s2 (1 r122 )
ns 22 (1 r122 )
2
Regresión Lineal
53
Consecuencias de la
multicolinealidad
Gran varianza de los estimadores
Cambio importante en las
estimaciones al eliminar o incluir
regresores en el modelo
Cambio de los contrastes al eliminar
o incluir regresores en el modelo.
Contradicciones entre el contraste F
y los contrastes individuales.
Regresión Lineal
54
Variables cualitativas como
regresores
Consumo
l/100Km
15
16
24
9
11
17
12
17
18
12
16
12
9
...
Cilindrada
cc
4982
6391
5031
1491
2294
5752
2294
6555
6555
1147
5735
1868
2294
...
Potencia
CV
150
190
200
70
72
153
90
175
190
97
145
91
75
...
Consumo =
+
+
0
Peso
kg
1144
1283
1458
651
802
1384
802
1461
1474
776
1360
860
847
...
1
CC +
Acel +
4
Aceleración
segundos
12
9
15
21
19
14
20
12
13
14
13
14
17
...
2
Origen
Europa
Japón
USA
Europa
Japón
USA
Europa
USA
USA
Japón
USA
Europa
USA
...
Pot +
JAP ZJAP
+
3 Peso
Origen
Europa
Japón
USA
Z JAP i
0 si i JAPON
1 si i JAPON
ZUSAi
0 si i USA
1 si i USA
Z EUR i
0 si i EUROPA
1 si i EUROPA
+
USA ZUSA +
Error
Regresión Lineal
55
Variables cualitativas
Consumo
l/100Km
15
16
24
9
11
17
12
17
18
12
16
12
9
...
Cilindrada
cc
4982
6391
5031
1491
2294
5752
2294
6555
6555
1147
5735
1868
2294
...
Consumo =
+
Regresión Lineal
Potencia
CV
150
190
200
70
72
153
90
175
190
97
145
91
75
...
0
4
+
1
Peso
kg
1144
1283
1458
651
802
1384
802
1461
1474
776
1360
860
847
...
CC +
Acel +
2
Aceleración ZJAP
segundos
12
0
9
1
15
0
21
0
19
1
14
0
20
0
12
0
13
0
14
1
13
0
14
0
17
0
...
...
Pot +
JAP ZJAP
+
3 Peso
ZUSA
ZEUR
0
0
1
0
0
1
0
1
1
0
1
0
1
...
1
0
0
1
0
0
1
0
0
0
0
1
0
...
+
USA ZUSA +
Error
56
Interpretación var. cualitativa
Consumo =
+
0
4
+
1
CC +
Acel +
2
Pot +
JAP ZJAP
+
3 Peso
+
USA ZUSA +
Error
Coches europeos: ZJAP = 0 y ZUSA = 0 REFERENCIA
Consumo =
0
+
1
CC +
2
Pot +
3 Peso
+
4
Acel + Error
Coches japoneses: ZJAP =1 y ZUSA = 0
Consumo =
0
+
JAP +
1
CC +
2
Pot +
3 Peso
+
4
Acel + Error
Coches americanos: ZJAP =0 y ZUSA = 1
Consumo =
0
+
USA +
1
CC +
2
Pot +
3 Peso
+
4
Acel + Error
Regresión Lineal
57
Interpretación del modelo
y
Americanos
Europeos
0+
Ref.
Japoneses
USA
0
0+
JAP
xi
Regresión Lineal
58
Regresión Lineal
59
Interpretación
El p-valor del coeficiente asociado a ZJAP
es 0.1956>.05, se concluye que no existe
diferencia significativa entre el consumo
de los coches Japoneses y Europeos
(manteniendo constante el peso, cc, pot y
acel.)
La misma interpretación para ZUSA.
Comparando R2 =0.821 de este modelo
con el anterior R2=0.8197, se confirma
que el modelo con las variables de
Origen no suponen una mejora sensible.
Regresión Lineal
60
Modelo de regresión con
variables cualitativas
En general, para considerar una variable
cualitativa con r niveles, se introducen en
la ecuación r-1 variables ficticias
z1i
0 i nivel1
, z 2i
1 i nivel1
0 i nivel 2
,
1 i nivel 2
, zr
0 i nivel r 1
1 i nivel r 1
1i
Y el nivel r no utilizado es el que actúa de
referencia
yi
0
x
1 1i
z
1 1i
k
z
2 2i
xki
z
r 1 r 1,i
ui
variablecualitativa
Regresión Lineal
61
Predicción
Nueva Observ. yh|xh
Media mh|xh
yh
mh
mh
xh
xh
yh
xh
Regresión Lineal
62
Predicción de la media mh
(Regresión simple)
mh
yh
xh
yh
N( 0
mh
xh
1 xh ,
2)
yh
0
1 xh y
1 ( xh x )
E[ yh ] E[ 0 1 xh ] 0 1xh mh
var[ yh ] var[ y
1 ( xh x )]
1 xh
0
( xh x ) 2
N mh ,
1
n
s x2
2
yh
x ) 2 var[ 1 ]
var[ y ] ( xh
2
x)
( xh
n
2
2
ns x2
Regresión Lineal
63
Predicción de la media mh
(Regresión múltiple)
mh
yh
mh
yh
)
xh
x'h
x
0
T
yh
2
N (mh ,
1 1h
k
Regresión Lineal
xkh
T
h
x'h , x'T
h]
E[ T x'h ] E[ T ]x'h
var[ y h ] var[ T x'h ]
2v
hh
(1, x1h , x2 h ,
, xkh )
h
E[ y
x'h
N mh ,
y
T
h
T
x'
h
x'
v
hh
(X
(X
T
T
X)
X)
T
h
x'
var[
1
x 'h 2
1
x 'h
T
T
x 'h
]x'h
vhh 2
64
Expresión alternativa para vhh
y bT ( x h
yh
x)
var[ yh ] var[ y bT (x h x)] var[ y ] (x h
2
n
~ ~
( x h x ) T ( XT X) 1 ( x h x )
2
x)T var[b](x h
~ ~
XT X
(S x
)
n
,
x)
2
n
(1 (x h
x ) T S x1 ( x h
1
(1 (x h
n
vhh
x))
T
1
x
x) S ( x h
x))
xh
x
vhh 1 / n
xh
x
vhh 1 / n
Regresión Lineal
65
Intervalos de confianza para la
media mh
yh
yh
2
N mh ,
mh
vhh
y h mh
s R vhh
yh
N (0,1)
tn
m
h
y t
h
vhh
1
(1 (xh
n
Regresión Lineal
vhh
k 1
s
/2 R
xh
vhh
Regresión simple
T
1
x
x) S ( x h
x))
vhh
1
( xh x ) 2
(1
)
2
n
sx
66
Predicción de una nueva
observación yh (Reg.Simple)
yh
yh
mh
xh
yh
yh
e~
h
0
N (mh ,
yh
yh
x
1 h
2
vhh )
2
N (mh ,
mh
xh
)
x
0
1 h
yh
E[e~h ] E[ yh ] E[ yh ] 0
var[e~h ] var[ yh ] var[ yh ]
2
2
e~h
N ( 0,
2
(1 vhh ))
vhh
Regresión Lineal
67
Predicción de una nueva
observación yh (Reg. Múltiple)
yh
yh
mh
xh
yh
e~h
y bT x h
yh
yh
E[~
eh ] E[ yh ] E[ yh ] 0
var[~
eh ] var[ yh ] var[ yh ]
yh
~
eh
Regresión Lineal
N (mh ,
N ( 0,
2
2
xh
vhh )
2
(1 vhh )
(1 vhh ))
68
Intervalos de predicción para
una nueva observación yh
e~h
N 0,
~
eh yh y h
yh y h
1 vhh
yh y h
2
(1 vhh )
yh
N (0,1)
tn k 1
s R 1 vhh
xh
y
h
y t
h
s
/2 R
1 vhh
Regresión Lineal
69
Límites de predicción
y
0
x
1 1
k
m
h
xk
y
y
h
y t
h
y t
h
s
s
/2 R
/2 R
1 vhh
x
Regresión Lineal
vhh
70
Diagnosis: Residuos
Y
X
e
Observados Previstos Residuos
y1
1
x11
x21
xk1
0
e1
y2
1
x12
x22
xk 2
1
e2
yn
1
x1n
x 2n
xkn
k
en
ei
yi
( 0
1x1i
k xki )
Regresión Lineal
71
Distribución de los residuos
Y
N (X ,
V
2
I)
e
(I V)Y
X(X T X) 1 X T
e Normal
E[e] (I V) E[Y] (I V)X
var[ e] (I V) var (Y)(I V)
e N (0, 2 (I V))
ei
Regresión Lineal
N (0,
2
0
2
(I V)
(1 vii ))
72
Distancia de Mahalanobis
Di2
(x i
x) T S x 1 (x i
x) (Dist. de Mahalanobis)
xi
xi
Midela distanciade x i a x
1
(1 (x i
n
x'Ti ( XT X) 1 x'i
vii
Di2
Di2
x
x
x ) T S x1 ( x i
0
0
x))
vii son los elementosdiagonalesde la matriz V
X(X T X) 1 XT
V
n
vii
n
vij v ji
j 1
2
ij
v
2
ii
v
n
vij2
vii (1 vii )
j 1, j i
1
n
0
j 1, j i
vii
1
Regresión Lineal
73
Residuos estandarizados
ei
N (0, (1 vii )
var(ei )
2
)
(1 vii ) 2
Cuando xi está próximo a x
vii
1/ n
Cuando xi está lejos de x
vii
1
var(ei )
var(ei ) 0
2
ei
0
Residuos estandarizados
ri
Regresión Lineal
ei
s R 1 vii
74
Hipótesis de normalidad
Herramientas de comprobación:
Histograma de residuos
Gráfico de probabilidad normal (Q-Q plot)
Contrastes formales (Kolmogorov-Smirnov)
probabilidad
Ejemplo de coches
99,9
99
95
80
50
20
5
1
0,1
-6
-4
-2
0
2
4
6
Residuos
Regresión Lineal
75
Comprobación de la linealidad
y homocedasticidad
Ambas hipótesis se comprueban
conjuntamente mediante gráficos de los
residuos
Frente a valores previstos
Frente a cada regresor.
En muchas ocasiones se corrige la falta
de linealidad y la heterocedasticidad
mediante transformación de las variables.
Regresión Lineal
log yi
0
1 1i
x
log yi
0
1
log x1i
k
xki ui
k
log xki ui
76
Residuos - Valores previstos
ei
Lineal y homocedástico
ei
No lineal y homocedástico
0
0
yi
yi
ei
ei
0
0
Lineal y no homocedástico
yi
No lineal y no homocedástico
yi
Regresión Lineal
77
Regresión Lineal
78
Funciones R relacionadas
Regresión Lineal
79
Ejemplo 1: Cerezos Negros
Se desea construir un
modelo de regresión para
obtener el volumen de
cerezo
en función de la
altura del tronco y del
diámetro del mismo a un
metro sobre el suelo. Se
ha tomado una muestra
de 31 árboles. Las
unidades de longitudes
son pies y de volumen
pies cúbicos.
Regresión Lineal
80
Cerezos negros: Datos
Árbol
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Diametro
8,3
8,6
8,8
10,5
10,7
10,8
11,0
11,0
11,1
11,2
11,3
11,4
11,4
11,7
12,0
12,9
Altura
70
65
63
72
81
83
66
75
80
75
79
76
76
69
75
74
Volumen
10,30
10,30
10,20
16,40
18,80
19,70
15,60
18,20
22,60
19,90
24,20
21,00
21,40
21,30
19,10
22,20
Regresión Lineal
Árbol
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Diametro
12,9
13,3
13,7
13,8
14,0
14,2
14,5
16,0
16,3
17,3
17,5
17,9
18,0
18,0
20,6
Altura
85
86
71
64
78
80
74
72
77
81
82
80
80
80
87
Volumen
33,80
27,40
25,70
24,90
34,50
31,70
36,30
38,30
42,60
55,40
55,70
58,30
51,50
51,00
77,00
81
Gráficos x-y
Regresión Lineal
82
Primer modelo:cerezos negros
Volumen
0
Regresión Lineal
1
Diametro
2
Altura Error
83
Diagnosis
Regresión Lineal
84
Transformación
vol k altura diámetro2
log( vol)
0
1 log( altura)
2
log( diámetro) error
Regresión Lineal
85
Diagnosis (modelo transformado)
Regresión Lineal
86
Interpretación
Se comprueba gráficamente que la distribución
de los residuos es compatible con las hipótesis
de normalidad y homocedasticidad.
El volumen está muy relacionada con la altura y
el diámetro del árbol (R2= 97.77%)
El modelo estimado
log(Vol) = -6.6 + 1.12 log(Alt) + 1.98 log(Diam.) + Error
es compatible con la ecuación vol=k Alt Diam2
La desviación típica residual es sR=0.081 que
indica que el error relativo del modelo en la
predicción del volumen es del 8.1%.
Regresión Lineal
87
Modelos de regresión lineal
1. La tabla muestra los mejores tiempos mundiales en Juegos Olı́mpicos hasta 1976 en carrera
masculina para distintas distancias.
y: tiempo (sg)
x: distancia (m)
9.9 19.8 44.26 103.5 214.9 806.4 1658.4 7795
100 200
400
800 1500 5000 10000 42196
(a) Estimar la regresión lineal de y sobre x y calcular la varianza residual y el coeficiente
de correlación.
(b) Obtener intervalos de confianza para la pendiente y varianza residual (α = 0.01).
(c) Analizar si la relación lineal es adecuada, transformando las variables si es necesario.
(d) Supóngase que en aquellas Olimpiadas hubiera existido una carrera de 500 metros.
Estimar el tiempo previsto para el record olı́mpico en dicha carrera, dando un intervalo
de confianza con α = 0.05.
2. Estimar por mı́nimos cuadrados los parámetros a y b de la ecuación y = a + bx2 con la
muestra de tres puntos siguientes (y, x) : (3, -1); (4, 0); (6,1).
3. Dada la recta de regresión ŷ = 3 + 5(x − 2) con r = 0.8, sˆR = 1, construir un intervalo de
confianza del 95% para la pendiente si n = 100.
4. Dado el modelo estimado con n = 25 datos, ŷ = 2 + 3(x − 4), ŝR = 5, con desviación tı́pica
del coeficiente de regresión S(βˆ1 ) = 0.5, calcular la desviación tı́pica de la predicción del
valor medio de y cuando x = 20.
5. Sir Francis Galton (1877) estudió la relación entre la estatura de una persona (y) y la estatura
de sus padres (x) obteniendo las siguientes conclusiones:
(a) Existı́a una correlación positiva entre las dos variables.
(b) Las estaturas de los hijos cuyos padres medı́an más que la media era, en promedio,
inferior a la de sus progenitores, mientras que los padres con estatura inferior a la
media en promedio tenı́an hijos más altos que ellos, calificando este hecho como de
”regresión” a la media.
Contrastar (α = 0.05) estas dos conclusiones con la ecuación ŷ = 17.8 + 0.91x resultante de
estimar un modelo de regresión lineal entre las variables (en cm.) descritas anteriormente
para una muestra de tamaño 100 si la desviación tı́pica (estimada) de β̂ 1 es 0.04.
6. La ley de Hubble sobre la expansión del universo establece que dadas dos galaxias la velocidad de desplazamiento de una respecto a la otra es v = Hd, siendo d su distancia y H
la constante de Hubble. La tabla proporciona la velocidad y la distancia de varias galaxias
respecto a la Via Láctea. Se pide:
1
Galaxia
Virgo
Pegaso
Perseo
Coma Berenices
Osa Mayor 1
Leo
Corona Boreal
Géminis
Osa Mayor 2
Hidra
Distancia
(millones años luz)
22
68
108
137
255
315
390
405
700
1100
Velocidad
(103 Km/s)
1.21
3.86
5.15
7.56
14.96
19.31
21.56
23.17
41.83
61.14
Tabla: Distancia y velocidad de desplazamiento de las distintas galaxias a la Via Lactea.
Nota: Obsérvese que según el modelo de Hubble la regresión debe pasar por el origen.
Tómese 1 año luz = 300 000 Km/seg x 31 536 000 seg = 9.46 1012 Km.
(a) Estimar por regresión la constante de Hubble.
(b) Como T = d/v = d/Hd = 1/H, la inversa de la constante de Hubble representa la
edad estimada del Universo. Construir un intervalo de confianza del 95% para dicha
edad .
9. Para establecer la relación entre el alargamiento en mm (Y ) producido en un cierto material
plástico sometido a tracción y la fuerza aplicada en toneladas por cm2 (X) se realizaron 10
experimentos cuyos resultados se muestran en la tabla
xi 0.20 0.50 0.60 0.70 0.90 1.00 1.20 1.50 1.60 1.70
yi 23
20
33
45
67
52
86
74
98
102
Tabla: Alargamiento yi (mm) producidos por la fuerza xi (Tm/cm2 ).
(a) Ajustar el modelo de regresión lineal E(Y |x) = β 0 + β 1 x y contrastar (α = 0.01) la
hipótesis de que, en promedio, por cada Tm/cm2 de fuerza aplicada es de esperar un
alargamiento de 50 milı́metros, sabiendo que la desviación tı́pica residual vale 10.55.
(b) Si el lı́mite de elasticidad se alcanza cuando x = 2.2 Tm/cm2 , construir un intervalo
de confianza al 95% para el alargamiento medio esperado en ese punto.
(c) Teniendo en cuenta que el alargamiento esperado cuando la fuerza aplicada es nula
debe ser nulo también, estimar el nuevo modelo E [Y |x] = βx con los datos anteriores
¿Cuál es el sesgo del estimador del parámetro de la pendiente si se estima según el
modelo del apartado 1?
2
10. La ecuación de regresión entre las ventas de un producto y y su precio x es ŷ = 320 − 1.2x,
ŝR = 2 y ŝy = 4. Si el número de datos ha sido n = 50, contrastar H0 : β 1 = −1 frente a la
alternativa H1 : β 1 < −1.
11. Se estudia la relación entre el tiempo de reparación (minutos) de ordenadores personales y
el número de unidades reparadas en ese tiempo por un equipo de mantenimiento con los
resultados mostrados en la siguiente tabla
unidades reparadas
tiempo de reparación
1 3 4
23 49 74
6
7
9
10
96 109 149 154
Se pide:
(a) Construir la recta de regresión para prever el tiempo de reparación y utilizarla para
construir un intervalo de confianza (α = 0.01) para el tiempo medio de reparación de
8 unidades.
(b) Construir un intervalo de confianza (α = 0.01) del tiempo de reparación para un lote
de 14 unidades.
(c) Si los tiempos de reparación fuesen medias de 10 datos. ¿Cual serı́a la recta de regresión?
13. Se realiza una regresión múltiple con tres regresores y se encuentra un coeficiente de correlación de 0.5 entre los residuos de la regresión y uno de los regresores. Interpretar este
resultado.
14. La matriz de varianzas de tres variables estandarizadas es la siguiente


1 0.8 0.6
 0.8 1 0.2 
0.6 0.2 1
Calcular la ecuación de regresión de la primera variable respecto a las otras dos.
15. Dos variables x1 y x2 tienen la siguiente matriz de varianzas
1 0.5
0.5 1
y las regresiones simples con y son ŷ = 0.75x1 ; ŷ = 0.6x2 . Calcular la regresión múltiple
entre y y las dos variables x1 , x2 sabiendo que la variable y tiene media cero y varianza
unidad.
16. Se realiza la regresión entre la variable dependiente y y tres regresores x1 , x2 y x3 . Posteriormente se decide realizar la regresión entre la variable y y los tres regresores estandarizados.
Explicar cuáles son las diferencias entre los resultados de una regresión y otra en cuanto a
los coeficientes estimados β̂ i , los residuos y el coeficiente de determinación, justificando la
respuesta.
3
17. La matriz de varianzas de las variables X1 , X2 e Y es


25 27
14
 27 36 19.2 
14 19.2 16
Siendo X 1 = 30, X 2 = 40, Y = 100 y el número de datos n = 10.
Se pide:
(a) Realizar la regresión simple entre Y (variable dependiente) y X1 , dando el intervalo de
confianza para la pendiente de la recta con α = 0.05. Hacer lo mismo con Y y X2 .
(b) Realizar la regresión múltiple entre Y (variable dependiente) y X1 , X2 , en desviaciones
a la media.
(c) Indicar si los coeficientes de la regresión anterior son significativos.
(d) Calcular R2 para los tres modelos, comentar los resultados obtenidos e indicar qué
modelo eligirı́a y por qué.
18. Para establecer la relación entre el voltaje de unas baterı́as y la temperatura de funcionamiento se han hecho unos experimentos cuyos resultados se muestran en la siguiente
tabla
Baterı́a
Temperatura
Voltaje
1
2
10 10
7.2 7.7
3
4
5
20 20 30
7.3 7.4 7.7
6
7
8
30 40
40
9.4 9.3 10.8
Se pide:
(a) Contrastar la hipótesis (α = 0.05) de que no existe relación lineal entre el voltaje y la
temperatura.
(b) Las lecturas 1,3,5 y 7 fueron realizadas con unas baterı́as de Cadmio y las 2,4, 6 y 8 con
baterı́as de Zinc. Introducir en el análisis anterior una variable cualitativa que tenga
en cuenta los dos tipos de baterı́as y contrastar si es significativa al 95%.
(c) Dar un intervalo de confianza para el voltaje de una baterı́a de Cadmio que va a trabajar
a 35◦ centı́grados. (Utilizar el modelo estimado en el apartado 2).
(d) Comprobar que se cumplen las hipótesis del modelo construido en los apartados anteriores.
19. ¿Cómo disminuirá la varianza teórica de los estimadores β̂ en el modelo de regresión lineal
al replicar las observaciones? (Por replicar se entiende el obtener un nuevo vector Y de la
variable respuesta manteniendo las X fijas).
4
20. Se ha estimado un modelo de regresión para la estatura (y) de un grupo de adultos y sus
estaturas a los 7 (x1 ) y 14 (x2 ) años. La desviación tı́pica residual obtenida es 5 cm y la
desviación tı́pica del coeficiente de x1 (estatura a los 7 años) resulta 2.4, siendo este efecto
no significativo al 95%. Sin embargo, un segundo modelo de regresión que incluya sólo a
esta variable (x1 ) conduce a una desviación tı́pica residual de 7 cm y a un coeficiente de
regresión de 2 con desviación tı́pica de 1. ¿Qué podemos concluir con estos resultados de la
correlación entre x1 y x2 ?
21. Se dispone de una muestra de 100 automóviles con información respecto a su consumo
(litros/100 km), peso (kg), potencia (CV), tipo de motor (I=inyección, NI=no inyección) y
nacionalidad (1=USA, 2=Alemania, 3=Japón, 4=Francia). Escribir la ecuación del modelo
de regresión lineal del consumo respecto al resto de las variables e interpretar el significado
de cada uno de los parámetros del modelo. Indicar cómo contrastar si la nacionalidad del
vehı́culo influye en el consumo.
22. Teniendo en cuenta que mediante variables cualitativas cualquier modelo de diseño experimental puede escribirse como un modelo de regresión, determinar la matriz V = X(X T X)−1 X T
de proyección y la varianza de un residuo eij para el modelo básico de análisis de la varianza
yij = µi + uij , i = 1, ..., I ; j = 1, ..., ni
Aplicarlo al caso de 3 grupos (I = 3), con 5 observaciones en el primer grupo, 4 en el segundo
y 3 en el tercero.
23. La variable y se relaciona con las variables x1 y x2 según el modelo E(y) = β 0 + β 1 x1 + β 2 x2 ;
no obstante se estima el siguiente modelo de regresión que no incluye la variable x2
ŷi = β̂ 0 + β̂ 1 x1i .
Justificar en qué condiciones el estimador β̂ 1 es centrado.
24. Se efectúa una regresión con dos variables explicativas E[y] = β 0 + β 1 x1 + β 2 x2 . La matriz
de varianzas de x1 y x2 es
2 1
1 3
¿Cuál de los dos estimadores β̂ 1 y β̂ 2 tendrá menor varianza?
25. Se estudia la relación entre los costes de fabricación totales en miles de pesetas (Y ), de 25
libros técnicos, la tirada en miles de ejemplares producidos (T ) y el número de páginas del
libro (N), encontrandose la relación
Y = 1400 + 900T + 4N
5
(a) Sabiendo que las desviaciones tı́picas (sin corregir por grados de libertad) de T y N
son 1.5 miles de ejemplares y 200 páginas respectivamente, y ŝR = 600, calcular un
intervalo de confianza del 90% para los efectos de T y N suponiendo que las variables
están incorreladas. Interpretar el resultado.
(b) Si el coeficiente de correlación entre las variables T y N es −0.5, ¿Puede admitirse la
hipótesis de que el coste asociado a la tirada es de 1.100.000 ptas. cada mil unidades?
(α = 0.05).
(c) Sabiendo que la desviación tı́pica (sin corregir por grados de libertad) de los costes de
fabricación es 2200 miles de pesetas, calcular el coeficiente de correlación múltiple y el
estadı́stico F para contrastar que ambas variables no influyen. Interpretar el resultado.
(d) Para estudiar cuánto encarecen los gráficos el precio se introduce en el modelo una
variable ficticia Z que toma el valor 1 en libros con gráficos y 0 en el resto, obteniéndose
el nuevo modelo estimado siguiente (desviaciones tı́picas entre paréntesis)
Y
= 1080 + 520Z + 840T + 3.8N
(100)
(16)
(0.97)
Interpretar el resultado.
26. Demostrar que el coeficiente de correlación múltiple en el modelo general de regresión es
igual al coeficiente de correlación lineal entre la variable observada y y la prevista ŷ.
27. Para 11 provincias españolas se conocen los siguientes datos:
Y = número de mujeres conductoras dividido por el número de hombres conductores.
X1 = porcentaje de mujeres que trabajan sobre el total de trabajadores de la provincia.
X2 = porcentaje de población que trabaja en el sector agrı́cola.
Si se denomina X = (1 X1 X2 ) a la matriz de regresores (1 es un vector de unos) se sabe que
(X T X)−1




5.1 −0.12 −0.05
−0.06
=  −0.12 30.8
0.08  (X T Y ) =  0.05 
−0.05 0.08 0.001
−9.45
ŝR = 0.03;
n
X
(yi − y)2 = 0.0645
i=1
Se pide:
(a) Estimar el modelo de regresión y realizar los contrastes individuales (α = 0.05). Interpretar la regresión.
(b) Calcular el coeficiente de determinación R2 y realizar el contraste de que las dos variables no influyen mediante el test F (α = 0.05).
6
(c) Se introducen dos nuevas variables en la regresión: X3 que representa el porcentaje
de población que trabaja en los servicios, y X4 el porcentaje de población que trabaja
en otras actividades distintas de agricultura y servicios. Explicar razonadamente cómo
será la regresión al introducir estas dos nuevas variables y los efectos de cada una de
ellas.
28. Con los datos de la tabla, se pide:
x -2
y 1.1
-2 -1 -1
0
1.3 2.0 2.1 2.7
0
1
1
2.8 3.4 3.6
2
2
3
3
4.0 3.9 3.8 3.6
(a) Estimar un modelo de regresión simple con y como variable dependiente y x como
regresor. Indicar si el modelo es apropiado, justificando la respuesta.
(b) Estimar el modelo
yi = β 0 + β 1 xi + β 2 x2i + ui
y realizar el contraste H0 : β 2 = 0.
(c) El resultado de la estimación del modelo que incluye el término x3 es,
ŷi = 2.81 + 0.80xi - 0.06x2i - 0.035x3i
(0.05)
(0.048)
(0.019)
(0.010)
con ŝR = 0.113 (entre paréntesis las desviaciones tı́picas de los estimadores). Realizar
el contraste general de regresión con α = 0.01. Seleccionar entre los tres el modelo más
adecuado, justificando la respuesta.
29. En un modelo de regresión simple se ha obtenido un coeficiente de correlación igual a −0.8.
Si el número de observaciones es n = 150, ȳ = 22 y la variabilidad total es 320. Construir
un intervalo de confianza al 95% para el valor medio de la variable dependiente (y) cuando
x (regresor) es igual a x̄. (Aproximar la distribución t de Student correspondiente por una
distribución normal, si Z
N(0, 1), P (Z ≤ 1.96) = 0.975).
30. En una planta piloto se obtiene un nuevo producto mediante un proceso quı́mico. Con el
fin de mejorar el rendimiento se emplean dos catalizadores distintos y se trabaja con tres
temperaturas diferentes. Los resultados del experimento son
Catalizador
A
B
Temperatura
200
300
400
115 125 130 140 110 120
115 105 135 145 100 110
(a) Contrastar si los factores Temperatura y Catalizador tienen efectos significativos. (α =
0.05)
(b) ¿Qué tratamiento se debe utilizar para obtener el mayor rendimiento, si se desea garantizar una probabilidad de error tipo I total, αT = 0.03?
7
(c) Estimar y contrastar el modelo de regresión simple entre el rendimiento y la temperatura. ¿Qué conclusiones obtiene? Proponga un modelo de regresión que subsane las
deficiencias encontradas.
31. El modelo de regresion múltiple se puede escribir en notación matricial
Y = Xβ + U
donde U es el vector de variables aleatorias que cumple las hipótesis de normalidad, independencia y homocedasticidad. Deducir razonadamente la distribución, media y matriz de
varianzas del vector de residuos e = Y − X β̂.
32. La empresa de bebidas gaseosas CIBELES quiere determinar la influencia sobre la presión
interna (yi ) en los botes de refresco de dos variables continuas (x1 , x2 ) y del tipo de bebida
(NARANJA=1, LIMON=2 y COLA=3). Para distintos valores de x1 y x2 y 20 botes de
cada sabor, ha medido la presión interna. El tipo de bebida se representa por las variables z1 ,
z2 y z3 qué identifican el sabor NARANJA, LIMON y COLA, respectivamente. El modelo
estimado de regresión de y con respecto a x1 , x2 , z2 y z3 es:
ŷ = 19.4 + 77.2x1 − 50.8x2 + 2.95z2 + 5.52z3 ;
donde
T
(X X)

−1


=


hatsR = 4.32

0.1772 −0.6909 −0.5043 −0.0605 −0.0896
−0.6909
5.8085
0.2541
0.1478
0.2444 

−0.5043
0.2541
5.0070 −0.0680
0.1216 

−0.0605
0.1478 −0.0680
0.1049
0.0546 
−0.0896
0.2444
0.1216
0.0546
0.1127
(a) Realizar los contrastes individuales con α = 0.01, indicando las variables que influyen
significativamente en la presión. Interpretar el resultado explicando el significado de
cada parámetro.
(b) Si se realiza una regresión entre la presión interna (yi ) y las dos variables continuas x1
y x2 se obtiene el siguiente modelo de regresión
ŷ = 23.86 + 65.1x1 − 56.3x2 ;
ŝR = 4.78.
Contrastar (α = 0.01) conjuntamente que el tipo de bebida no influye. (H0 : α2 = α3 =
0 frente a H1 : α2 ó α3 es distinto de cero).
(c) ¿Existe diferencia significativa en las presiones internas de los botes de LIMON y
COLA? (α = 0.01)
33. Estimar por máxima verosimilitud los parámetros β 1 y β 2 del modelo
yi = β 1 x1i + β 2 x22i + ui
; ui
N(0, σ).
¿En qué condiciones los estimadores obtenidos por máxima verosimilitud son iguales que los
obtenidos por mı́nimos cuadrados?
8
34. Obtener la relación entre el coeficiente de determinación R2 y el coeficiente de determinación
2
corregido R . ¿ Que ventajas presenta el segundo frente al primero ?
35. Con el fin de reducir el tiempo de secado se han realizado 20 ensayos con cementos de
distintas caracterı́sticas. El ajuste por mı́nimos cuadrados de la ecuación de regresión entre
el tiempo de secado y una de las variables x1 es
ŝR = 12.8, R2 = 0.37
ŷ = 17.1 + 2.9x1 ,
(a) Obtener el intervalo de confianza al 95% para el parámetro de la pendiente de la recta
e indicar si su efecto es significativo.
(b) Incluir en el modelo de regresión otra variable independiente x2 , sabiendo que su varianza muestral es s22 = 9.2, la covarianza entre las dos variables independientes es
s12 = −3.35 y la covarianza entre el tiempo de secado y la nueva variable s2y = 9.55.
Realizar los contrastes individuales para los parámetros de x1 y x2 .
(c) Un estudio teórico del problema indica que el efecto de las dos variables es igual y que
por tanto, la ecuación de regresión deberı́a ser
ŷ = b̂0 + b̂1 (x1 + x2 ).
Con la información de los apartados anteriores, obtener b̂1 y contrastar si la pendiente
de la recta es significativamente distinta de cero.
36. Explicar cómo contrastar que dos o más coeficientes en un modelo de regresión múltiple son
simultanáneamente nulos.
37. En el análisis de regresión simple entre dos variables, se considera como importante desde
el punto de vista práctico, una correlación entre las dos variables igual o superior a r = 0.1.
Determinar el número mı́nimo de observaciones con las que se debe estimar el modelo de
regresión para que una correlación igual a 0.1, implique que el regresor tiene un efecto
significativo sobre la variable dependiente. (Aproximar la distribución t de Student correspondiente por una distribución normal, si Z
N(0, 1), P (Z ≤ 1.96) = 0.975).
38. Interpretar geométricamente el problema de estimación por mı́nimos cuadrados en regresión
múltiple. Demostrar que los residuos del modelo se obtienen mediante la expresión e =
P Y , donde Y es el vector correspondiente a la variable dependiente y P es una matriz de
dimensión n × n. Determinar P en términos de la matriz X de los regresores. A partir de
la expresión anterior, obtener la distribución de probabilidad de los residuos, la media y la
matriz de varianzas.
39. Una de las etapas de fabricación de circuitos impresos requiere perforar las placas y recubrir
los orificios con una lámina de cobre mediante electrólisis. Una caracterı́stica esencial del
proceso es el grosor de la capa de cobre. Se han realizado 12 experimentos para evaluar
el efecto de 7 variables, X1 : Concentración de Cobre, X2 : Concentración de Cloruro, X3 :
Concentración de Ácido, X4 : Temperatura, X5 : Intensidad, X6 : Posición y X7 : Superficie
de la placa. Cada variable se ha estudiado a dos niveles. Las condiciones experimentales y
los resultados de cada experimento se muestran en la tabla.
9
X1 X2 X3 X4 X5 X6 X7
1
1 -1
1
1
1 -1
1 -1
1
1
1 -1 -1
-1
1
1
1 -1 -1 -1
1
1
1 -1 -1 -1
1
1
1 -1 -1 -1
1 -1
1 -1 -1 -1
1 -1
1
-1 -1 -1
1 -1
1
1
-1 -1
1 -1
1
1 -1
-1
1 -1
1
1 -1
1
1 -1
1
1 -1
1
1
-1
1
1 -1
1
1
1
-1 -1 -1 -1 -1 -1 -1
Y
2.13
2.15
1.67
1.53
1.49
1.78
1.80
1.93
2.19
1.61
1.70
1.43
Responder a las siguientes preguntas aplicando el modelo de regresión múltiple, teniendo en
cuenta que X T X = 12I8 , donde I8 es la matriz identidad de 8 × 8.
(a) Estimar el modelo de regresión múltiple
yi = β 0 + β 1 x1i + β 2 x2i + β 3 x3i + β 4 x4i + β 5 x5i + β 6 x6i + β 7 x7i + ui .
Obtener la descomposición de la variabilidad del modelo y realizar el contraste
H0 : β 1 = β 2 = β 3 = β 4 = β 5 = β 6 = β 7 = 0
frente a la hipótesis alternativa H1 : algún β j es distinto de cero.
(NOTA.: X T Y = (21.41, −0.03, 0.01, −0.23, 1.69, 2.35, −0.09, −0.19)T )
(b) Realizar cada uno de los contrastes individuales e indicar qué variables tienen efecto
significativo.
(c) Eliminar del modelo del apartado 1 todas las variables no significativas. Estimar el
modelo y contrastar sus coeficientes. Interpretar los resultados del experimento.
40. Una medida crı́tica de calidad en la fundición de llantas de aluminio por inyección es la
porosidad. Se ha realizado un diseño experimental para analizar la porosidad (Y ) en función
de la temperatura (T ) del aluminio lı́quido y de la presión (P ) con que éste se inyecta al
molde. Se han realizado n=16 experimentos y el modelo obtenido ha sido
ŷ
=
2.84 +
(.048)
+
0.26
T2 +
(.048)
0.59 T
(.048)
0.30 P 2
(.048)
-
0.031
P
(.048)
0.22 T P
(.068)
Entre paréntesis se proporciona la desviación tı́pica estimada para cada uno de las estima2
ciones de los parámetros del modelo. Además ŝR = 0.137 y R = 0.9267. Las condiciones
experimentales se eligieron de forma que los cinco regresores utilizados en el modelo están
incorrelados.
10
(a) Realizar el contraste F general de regresión y los contrastes individuales de todos los
coeficientes del modelo, indicando cuál es significativamente distinto de cero.
(b) Demostrar que si los regresores estan incorrelados, al eliminar alguno del modelo,
las estimaciones de los restantes no varı́an. Además, si se elimina el regresor j, con
parámetro estimado β̂ j , la variabilidad no explicada del nuevo modelo V NE1 es igual
2
a V NE0 + ns2j β̂ j , donde V NE0 es la variabilidad no explicada del modelo con todos
2
los regresores. Obtener ŝR y R para el modelo que únicamente incluye los parámetros
significativos.
(c) Determinar en qué condiciones de presión y temperatura la porosidad es mı́nima según
el modelo anterior y dar un intervalo para predicción de la porosidad media en estas
condiciones. (Si t es la temperatura medida en grados centı́grados (0 C) y p la presión
en kg/cm2 ,
P
T = (t − 650)/10
y P = (pP
− 975)/25. En
estas unidades se cumple que ni=1 Ti = 0,
P
P
P
n
n
n
n
2
2
i=1 Ti Pi = 0)
i=1 Pi = 8,
i=1 Ti = 8,
i=1 Pi = 0,
41. Demostrar que cuando todos los regresores están incorrelados,
el coeficiente de determinación
Pk
2
2
de un modelo de regresión múltiple cumple R = j=1 rj , donde k es el número de regresores
y rj el coeficiente de correlación entre el regresor j y la variable dependiente.
42. Explicar el concepto de multicolinealidad en regresión múltiple, cómo se identifica y cuáles
son sus efectos sobre (a) los estimadores β̂ i , (b) los residuos y (c) las predicciones.
43. Demostrar que en un modelo de regresión simple y y el estimador de la pendiente β̂ 1 son
independientes. Utilizar esta propiedad para calcular la varianza de β̂ 0 = y − β̂ 1 x.
44. La masa M de un cristal de hielo depositado en una cámara a temperatura (-5o C) y humedad
relativa constante crece según la ecuación M = αT β , donde T es el tiempo y α y β son
parámetros desconocidos. La relación anterior se linealiza con la transformación logarı́tmica,
estimándose el siguiente modelo
log M = log α + β log T + u
donde el término añadido u son los errores experimentales, que se consideran aleatorios e
independientes con distribución normal, N(0,σ 2 ). Diez cristales del mismo tamaño y forma se
introdujeron en una cámara, extrayéndose secuencialmente según unos tiempos previamente
establecidos. Para determinar la influencia del tipo de cámara, se repitió exáctamente el
experimento en una segunda cámara. Los valores de ŝR para la cámara 1 y 2 son 0.64 y
0.50, respectivamente. Los modelos estimados para cada cámara, X T X y (X T X)−1 son:
log M1 = −7.30 + 2.40 log T
log M2 = −5.74 + 2.03 log T
T
(X X)
−1
=
11
T
X X=
18.27 −3.89
−3.89 0.835
10.00 46.66
46.66 218.9
(a) Contrastar con nivel de significación 0.05 si los dos modelos tienen la misma pendiente.
Lo mismo para la ordenada en el origen. (NOTA.- Aceptar que la varianza de los
dos modelos es la misma y estimarla como el promedio de las dos varianzas residuales
calculadas.)
(b) Un modelo de regresión múltiple Y = Xβ + U, se replica, es decir se obtienen dos
vectores de variables respuesta Y1 , Y2, para los mismo regresores (matriz X). Demostrar
que si β̂ 1 y β̂ 2 son los resultados de la estimación de β utilizando por separado la variable
Y1 e Y2 ; entonces el estimador de β con todos los datos es (β̂ 1 + β̂ 2 )/2.
(c) Estimar un único modelo con los datos de las dos cámaras. Sabiendo que Y T Y = 306.8,
donde Y = log M, dar un intervalo de confianza al 99% para los dos parámetros.
45. El molibdeno se añade a los aceros para evitar su oxidación, pero en instalaciones nucleares
presenta el inconveniente de ser el causante de gran parte de los productos radioactivos. Se
ha realizado un experimento para determinar el grado de oxidación del acero en función del
porcentaje de molibdeno. Además se ha tenido en cuenta el efecto del tipo de refrigerante
utilizado (R1 , R2 ). Los resultados se muestran en la tabla.
Refrig. 0.5%
R1
26.2
R2
34.8
R1
33.2
R2
43.0
Media 34.3
Molibdeno (%)
1% 1.5%
23.4 20.3
31.7 29.4
31.3 28.6
40.0 31.7
31.6 27.5
2% Medias
23.3
23.3
26.9
30.7
29.3
30.6
33.3
37.0
28.2
30.4
(a) Escribir un modelo de regresión que incluya el porcentaje de molibdeno y el tipo de refrigerante como regresores; estimar el modelo e indicar qué parámetros son significativos
(α = 0.05)).
(b) Los experimentos relativos a las dos primeras filas se realizaron en un tipo de instalación
y los correspondientes a las dos últimas en otra distinta. Escribir un nuevo modelo que
incluya este aspecto. Comprobar que este nuevo regresor está incorrelado con los dos
anteriores. Estimar el nuevo modelo.
(c) Demostrar que en un modelo con los regresores incorrelados, la eliminación de uno
de ellos no influye en el valor de los estimadores β̂ i , (i 6= 0) restantes. ¿ Influye en
la varianza residual y en los contrastes ? Explicar este efecto en función de que el
parámetro β del regresor eliminado sea o no nulo.
46. Demostrar que en un modelo de regresión múltiple estimado por máxima verosimilitud, los
residuos cumplen
n
X
ej xij = 0,
j=1
donde [xi1, xi2, ..., xin, ] es cualquier regresor del modelo. Obtener la distribución conjunta
del vector de residuos. Si σ 2 es la varianza teórica de la componente aleatoria del modelo,
indicar en que circuntancias la varianza de un residuo es mayor que σ 2 .
12
47. Se dispone de una muestra de 86 vehı́culos, de los cuales 31 son japoneses (J), 41 norteamericanos (N) y 14 europeos (E). La media y desviación tı́pica del consumo de gasolina (en litros
cada 100 Km) para los coches japoneses es y J = 9.1781, b
sJ = 1.42, para los norteamericanos
y N = 9.7274, b
sN = 1.25 y para los europeos y E = 10.64, b
sE = 1.36.
(a) Suponiendo que los vehı́culos escogidos son muestras aleatorias independientes y que
pueden aplicarse las hipótesis de normalidad y homocedasticidad, contrastar la hipótesis
de que el lugar de fabricación no influye en el consumo de combustible. ¿Existe algún
grupo con un consumo significativamente menor que los otros dos?
(b) Los coches tienen caracterı́sticas muy diferentes (peso, potencia,...) que deben ser
tenidas en cuenta para hacer la comparación anterior. Con esa finalidad, se ha ajustado
el siguiente modelo de regresión:
yb = 3.305 + 0.843 Pot + 3.829 Peso + 0.440 ZJ + 1.127 ZE sb2R = 0.506,
R2 = 75.7%
donde (X T X)−1 es:


4.791e − 1
5.054e − 2 −3.794e − 1 −9.157e − 2 −4.682e − 2
 5.054e − 2
1.595e − 1 −1.931e − 1 −3.443e − 3 −1.262e − 2 



 −3.794e − 1 −1.931e − 1
4.646e
−
1
5.210e
−
2
2.865e
−
2


 −9.157e − 2 −3.443e − 3
5.210e − 2
6.667e − 2
2.744e − 2 
−4.682e − 2 −1.262e − 2
2.865e − 2
2.744e − 2
9.759e − 2
dónde la variable dependiente es el consumo, Pot (potencia) está expresada en unidades
de 100 Cv, el Peso en Toneladas, ZJ toma el valor 1 si el coche es japonés y cero en
los demás, y ZE toma el valor 1 para los coches europeos y cero en los demás. Realizar
el contraste general de regresión para el modelo anterior e interpretar los coeficientes
estimados.
(c) Con el modelo de regresión anterior realizar los tres contrastes siguientes:
(c.1) No existe diferencia en el consumo de los coches japoneses y europeos.
(c.2) No existe diferencia en el consumo de los coches japoneses y norteamericanos.
(c.3) No existe diferencia en el consumo de los coches europeos y norteamericanos.
Comparar los resultados con los obtenidos en el apartado 1, explicar a qué se deben las
diferencias y justificar cuál es el modelo más adecuado para hacer las comparaciones.
48. El modelo de regresión múltiple con n observaciones y k + 1 variables independientes (incluyendo la constante β 0 ) se puede escribir en notación matricial como
Y = Xβ + U,
donde U es el vector de variables aleatorias que cumple las hipótesis de normalidad, independencia y homocedasticidad y la matriz de los regresores X es de dimensión n × (k + 1).
Demostrar que si se transforma linealmente la matriz X, esto es, W = XA, donde A es
cualquier matriz cuadrada de dimensión (k + 1) × (k + 1) y rango máximo, entonces la
regresión de Y con la nueva W proporciona las mismas predicciones y los mismos residuos.
Justificar geométricamente este resultado.
13
49. La resistencia a la tracción (y) de una aleación metálica en función de la temperatura de
templado (x) se ha ajustado con una ecuación de regresión para 30 observaciones resultando:
ŷ = 276.1 + 1.9x, ŝR = 15.7, R2 = 0.43
Se puede concluir con una confianza del 95% que la temperatura de templado tiene efecto
significativo en la resistencia a la tracción.
50. En Cosby Creek, una ciudad al sur de las montañas Apalaches, se ha hecho un estudio para
determinar cómo el pH y otras medidas de acidificación del agua se ven afectadas durante
las tormentas. En concreto se han obtenido 17 datos durante cada una de las tres tormentas
monitorizadas para un total de 19 variables, aunque en este análisis se analizarán solo 2, el
pH y el denominado Weak Acidity (WA). Se ha estimado el modelo de regresión múltiple
del valor pH con respecto a la variable WA y para cada una de las tres tormentas. Las
tormentas se representan con las variables ficticias z1 , z2 y z3 que identifican respectivamente
la tormenta 1, 2 y 3. El modelo estimado de regresión de y con respecto a WA, z1 , z2 y z3
es:
c = 5.77 − 0, 00008W A + 0, 998z1 + 1, 65z2 − 0, 005z1 W A − 0, 008z2W A,
pH
(0,000727)
(0,4664)
(0,4701)
(0,0014)
R2 = 0, 866
(0,0016)
Entre paréntesis las deviaciones tı́picas estimadas de los estimadores de los parámetros correspondientes.
(a) Realice el contraste general de regresión y los contrastes individuales con α = 0, 05
indicando las variables que influyen significativamente en el pH. Interprete el significado
de cada parámetro.
(b) Proporcione sendos intervalos de confianza al 95% para los parámetros de las interacciones z1 W A y z2 W A. ¿Qué conclusiones pueden extraerse? ¿Se puede simplificar el
modelo?
51. Dos becarios del Departamento de Ciencias Sociales están interesados en el estudio de la
Tasa de Mortalidad Infantil (TMI). Para ello, han recogido en 107 paı́ses dicha magnitud
ası́ como la alfabetización (A), el PIB y la población (Pob) en cada uno de ellos.
Las medias y desviaciones tı́picas corregidas de estas 4 variables son:
Media
DT corregida
TMI
42.67
38.3
A
PIB
Pob
78.34 5831.4
48501
22.88 6537.24 147.991
(a) Si el coeficiente de correlación entre TMI y A vale -0.9005 estime el modelo de regresión
simple en el que TMI es la variable respuesta y A la variable explicativa y contraste si
la pendiente estimada es significativa.
(b) Los becarios han estimado un modelo de regresión múltiple en que la variable dependiente es TMI y las variables independientes son A, PIB y Pob. Observando que la
diagnosis del modelo es inadecuada. Estime el modelo de regresión múltiple entre TMI
(variable dependiente) y los regresores A, log(PIB) y log(Pob). Para ello se proporciona:
14
e ′ X)
e −1
(X


0.0259 −0.0499 0.0001
= 10−3 −0.0499 0.3186 0.0007
0.0001
0.0007 0.0004


−8.3651
e ′ Ye ) = 104 −1.7007
(X
5.1293
e la matriz de estos 3 últimos regresores en desviaciones a la media e Ye el vector
siendo X
respuesta en desviaciones a la media. ¿Son significativos los coeficientes estimados?
c. Para el modelo del apartado anterior realice el contraste general de regresión. ¿Encuentra contradicciones entre el resultado de los contrastes individuales del apartado 2
y el del apartado 3? Justifique la respuesta.
d. Los paı́ses objeto del estudio se pueden clasificar en desarrollados y no desarrollados.
Para ello se introduce la variable cualitativa Z que toma valor 0 si el paı́s es desarrollado
y 1 si no lo es. El modelo resultante se presenta a continuación:
T MI = 138.2 − 1.1A − 9.6 log(P IB) + 3.3Z
con sb2R = 196.3
Todos los coeficientes estimados resultan significativos. Interprete dichos coeficientes y elija
de manera razonada el mejor modelo de entre los propuestos en el segundo y cuarto apartados
NOTA: Utilice α = 0.05 para todos los contrastes que sean necesarios.
52. Se ha realizado la regresión entre la anchura y la longitud del pie en centı́metros con datos
de chicos y chicas de cuarto curso de la enseñanza secundaria. En la tabla se proporciona el
resultado de la regresión. En el modelo se ha incluido una variable cualitativa que toma el
valor 1 si la observación corresponde a una chica y 0 si es a un chico. Interpreta el resultado
del análisis.
Multiple Regression Analysis
----------------------------------------------------------------------------Dependent variable: Anch
----------------------------------------------------------------------------Standard
T
Parameter
Estimate
Error
Statistic
P-Value
----------------------------------------------------------------------------CONSTANT
4,29977
1,12692
3,81551
0,0005
Long
0,21311
0,048554
4,38913
0,0001
Chica
-0,272394
0,127844
-2,13067
0,0402
----------------------------------------------------------------------------Analysis of Variance
15
----------------------------------------------------------------------------Source
Sum of Squares
Df Mean Square
F-Ratio
P-Value
----------------------------------------------------------------------------Model
4,60164
2
2,30082
16,41
0,0000
Residual
4,90599
35
0,140171
----------------------------------------------------------------------------Total (Corr.)
9,50763
37
R-squared = 48,3994 percent
53. Según la ecuación de los gases ideales, la presión ejercida por un gas a volumen y temperatura
constante es proporcional a la masa. Se puede utilizar el siguiente procedimiento para estimar
el peso molecular de un gas. Se almacena el gas en un recipiente de volumen constante, y se va
soltando poco a poco gas, variando la presión, pero manteniendo la temperatura constante.
En la tabla adjunta se proporcionan mediciones de la presión (con respecto a la atmosférica)
y de la masa del gas para el árgon.
Presión (psi)
52
49
44
39
34
29
25
21
19
19
11
0
Masa (g)
1, 028
0, 956
0, 88
0, 793
0, 725
0, 645
0, 593
0, 526
0, 5
0, 442
0, 373
0, 21
(a) Para estimar el peso molecular del árgon a partir de los datos, se propone el siguiente
modelo de regresión
Pi = αmi + ui , con ui ∼ N(0, σ 2 ).
Obtener el estimador de máxima verosimilitud del parámetro α
(b) Realizar el contraste H0 : α = 50 frente a H1 : α 6= 50 con nivel de significación 0.05.
(c) Para el modelo del apartado 1, obtener un intervalo de predicción para la presión cuando
la masa es igual a 1 gramo.
(d) Se considera también el modelo alternativo
Pi = β 0 + β 1 mi + ui con ui ∼ N(0, σ 2 ).
16
Obtener la varianza del estimador de E[Ph |mh ], es decir del valor medio de la presión Ph
para una masa dada mh con ambos modelos. Si el modelo verdadero fuese el del primer
apartado, ¿qué efecto tendrı́a sobre la predicción adoptar el modelo alternativo?
54. Se ha estimado un modelo de regresión con dos variables independientes y 150 observaciones
obteniéndose la siguiente ecuación:
ybi = −1.17 + 0.025 log x1 + 0.59 log x2 ,
sb2R = 2.48
b ,β
b ]T para el modelo propuesto es
La matriz de varianzas estimada de bb = [β
1
2
−1
.253 .201
T
2
X̃ X̃
sbR =
.
.201 .288
realiza el contraste general de regresión con α = 0.05:
H0 : β 1 = β 2 = 0
H1 : algún β i es distinto de cero
55. En el modelo de regresión
yi = β 0 + β 1 X1i + β 2 X2i + ui
con las hipótesis habituales, explicar como se contrasta
H0 :
H1 :
β1 = β2
β 1 6= β 2
56. Demostrar que en el modelo de regresión múltiple con k regresores y constante, el estadı́stico
que contrasta H0 : β 0 = β 1 = β 2 = · · · = β k = 0 frente a H1 : algún β i 6= 0, si H0 es cierta
es:
F =
n−k−1
Y TV Y
T
Y (I − V )Y k + 1
Fk+1,n−k−1
donde V = X(X T X)−1 X T e I es la matriz identidad de dimensión n × n.
57. En la tabla siguiente se muestra el resultado de un experimento para relacionar el calor
generado en el proceso de endurecimiento del 13 muestras de cemento en función de su
composición. Los regresores Xi corresponden al porcentaje de 4 componentes de la mezcla.
17
Fila
X1
7
1
11
11
7
11
3
1
2
21
1
11
10
1
2
3
4
5
6
7
8
9
10
11
12
13
Regresores
X2 X3 X4
26
6 60
29 15 52
56
8 20
31
8 47
52
6 33
55
9 22
71 17
6
31 22 44
54 18 22
47
4 26
40 23 34
66
9 12
68
8 12
Calor
Y
78.5
74.3
104.3
87.6
95.9
109.2
102.7
72.5
93.1
115.9
83.8
113.3
109.4
Modelo II
Residuo vii
-1.574 0.25
1.049 0.26
-1.515 0.12
-1.658 0.24
-1.393 0.08
4.048 0.11
-1.302 0.36
-2.075 0.24
1.825 0.18
1.362 0.55
3.264 0.18
0.863 0.20
-2.893 0.21
Modelo I
Parámetros
Constante
X1
X2
X3
X4
Estimación
62.4
1.55
0.51
0.10
-0.14
Modelo II
Desv. Tı́p.
Estimadas
70.1
0.74
0.72
0.75
0.71
t
0.89
2.08
0.70
0.13
-0.20
Parámetros
Constante
X1
X2
Fuentes
Grados
Lib.
Explic.
Residual
Total
2667.9
47.8
2715.7
4
8
12
t
23.0
12.1
14.4
Análisis de la Varianza
Análisis de la Varianza
Variabilidad
Estimación
52.6
1.46
0.66
Desv. Tı́p.
Estimadas
2.28
0.12
0.045
Var.
F
Fuentes
Variabilidad
667.0
5.98
111.5
Explic.
Residual
Total
2657.8
57.9
2715.7
Grados
Lib.
2
10
12
Var.
F
1328.9
5.8
229.5
En las tablas se proporcionan dos modelos de regresión lineal, con las estimaciones de los
parámetros, las desviaciones tı́picas estimadas de éstos y los estadı́sticos t de los contrastes
individuales. Debajo se incluyen las tablas de análisis de la varianza de cada modelo.
(a) Realizar los contrastes H0 : β i = 0 frente H1 : β i 6= 0 para los distintos parámetros en
los dos modelos. Realizar el contraste conjunto H0 : β 3 = β 4 = 0 frente H1 : alguno de
los dos es 6= 0. ¿Se puede concluir con éstos datos que X4 no influye significativamente
en el calor Y ?
(b) Estimar el modelo de regresión simple del calor Y y la variable explicativa X4 ¿Influye
significativamente X4 en el calor Y ? Analizar este resultado e interpretarlo teniendo
en cuenta el resultado del apartado anterior.
(c) En la tabla superior se muestran los residuos del modelo II y los elementos de la
diagonal de la matriz V = X(X T X)−1 X T . Indicar los residuos con mayor y menor
varianza, justificando la respuesta. Si se vuelve a repetir los experimentos en estas dos
18
condiciones, dar un intervalo para la predicción de los nuevos valores de la variable
dependiente (usar α = 0.05).
58. En un estudio de regresión simple con 35 observaciones ha resultado el siguiente modelo
ŷ = 0.12 + 7.6 log(x),
ŝR = 1.2,
R2 = 0.37
Obtener el intervalo de confianza al 95% para el parámetro de la pendiente e indicar si su
efecto es significativo.(El percentil 0.975 de la distribución t de Student con 33 grados de
libertad es 2.03)
59. Los datos siguientes corresponden a la pérdida (P) por abrasión en gr/h y su medida de
dureza (D) en grados Shore para 15 gomas de caucho de alta resistencia a la tensión (A) y
otras 15 gomas de caucho con resistencia a la tensión baja (B):
A
A
A
A
B
B
B
B
D
D
P
P
D
D
P
P
75
53
128
221
45
89
372
114
55 61 66 71 71 81 86
60 64 68 79 81 56
206 175 154 136 112 55 45
166 164 113 82 32 228
68 83 88 59 71 80 82
51 59 65 74 81 86
196 97 64 249 219 186 155
341 340 283 267 215 148
Escribir el modelo estadı́stico, indicar los parámetros y explicar el procedimiento de estimación para estudiar con estos datos simultáneamente el efecto de la dureza y de la resistencia a la tensión (alta o baja) en las pérdidas por abrasión. Indicar cómo contrastar con el
modelo propuesto que “las gomas de caucho con baja resistencia a la tracción tienen por
término medio mayor pérdida que las gomas con resistencia a la tracción baja.” (Nota.- No
se pide ningún cálculo numérico, los datos se presentan para ilustrar y describir el problema
de forma precisa).
60. Sea x1 la altura del tronco de un árbol y x2 el diámetro del mismo en su parte inferior. El
volumen y del tronco de árbol puede ser calculado aproximadamente con el modelo
yi = αx1i x22i + ui ,
según el cual, el volumen del tronco es proporcional al volumen de un cono con las medidas
x1i , x2i , siendo α el parámetro (desconocido) de proporcionalidad, más una componente
de error aleatorio ui . La tabla siguiente contiene los datos (en metros y metros cúbicos)
correspondientes a una muestra aleatoria de 15 troncos de una variedad de pino.
19
Obs.
1
2
3
4
5
6
7
8
x1i
10,1
11,3
20,4
14,9
23,8
19,5
21,6
22,9
x2i
0,117
0,13
0,142
0,193
0,218
0,236
0,257
0,269
x1i x22i
0,14
0,19
0,41
0,56
1,13
1,09
1,43
1,66
yi
0,062
0,085
0,204
0,227
0,47
0,484
0,623
0,722
x1i
19,8
26,8
21
27,4
29
27,4
31,7
Obs.
9
10
11
12
13
14
15
x2i
0,297
0,328
0,351
0,376
0,389
0,427
0,594
x1i x22i
1,75
2,90
2,60
3,90
4,40
5,00
11,2
yi
0,821
1,280
1,034
1,679
2,073
2,022
4,630
(a) Estimar α por máxima verosimilitud suponiendo que las variables ui tienen distribución
normal de media cero, con la misma varianza e independientes.
(b) Un tronco tiene una altura de 20 metros y un diametro de 0.25 metros, dar un intervalo
de predicción de su volumen (95% de confianza). La varianza residual del modelo es
0,0058.
(c) En el análisis de los residuos se observa que la varianza de los errores crece con el
volumen del tronco. Para obtener homocedasticidad se propone el siguiente modelo
transformado utilizando logaritmos neperianos,
log yi = β 0 + β 1 log x1i + β 2 log x2i + ui
El resultado de la estimación es:
Parámetro
β0
β1
β2
Estimación
-1,45
1,14
1,86


0, 1250
0, 0212 −0, 0317
cb =  0, 0212
0, 0082 −0, 0051 
M
β
−0, 0317 −0, 0051
0, 0042
y
cb = b
siendo M
s2R (X T X)−1 (X es la matriz de los regresores transformados según el
β
modelo) La transformación logarı́tmica del modelo inicial (αx1i x22i ) implicarı́a que β 1 =
1 y β 2 = 2. Contrastar (nivel de significación 0.05) si estos dos valores son aceptables.
(d) Con este modelo, dar un intervalo de predicción (95% de confianza) para el volumen
del tronco del apartado 2 si la varianza residual es 0,0031.
61. La cantidad máxima yi de cierto compuesto disuelta en un litro de agua a temperatura xi
sigue el modelo de regresión simple,
yi = β 0 + β 1 xi + ui ,
dónde ui cumple las hipótesis de normalidad, homocedasticidad (Var(ui ) = σ 2 ) e independencia. Una muestra de n disoluciones diferentes han proporcionado los valores (yi , xi ).
′
Además se han medido las cantidades disueltas y1′ , y2′ , ..., ym
en otra muestra de m disoluciones que se encontraban a la misma temperatura x0 . El valor x0 es desconocido. Estimar
por máxima verosimilitud los parámetros β 0 , β 1 , σ 2 y x0 utilizando las n + m observaciones.
20
62. Explicar en qué consiste el problema de la multicolinealidad en el modelo de regresión: cómo
se detecta, cómo se puede corregir y cuáles son sus efectos.
63. Ciertas propiedades del acero se mejoran sumergiéndolo a alta temperatura (T0 = 1525
o
F ) en un baño templado de aceite (t0 = 95 o F ). Para determinar la influencia de las
temperaturas del acero y del baño de aceite en las propiedades finales del material se han
elegido tres valores de la temperatura del acero y tres del baño de aceite,


 1450 o F
 70 o F
Temperatura acero (T ) 1525 o F
Temperatura aceite (t) 95 o F


o
1600 F
120 o F
y se han realizado los siguientes experimentos:
x1i
x2i
yi
0
0
0
0
-1
1
-1
0
0
0
0
-1
-1
1
49.2 49.4 47.0 49.5 28.2 88.6 54.9
1
0
0
-1
1
1
-1
1
0
0
31.3 59.2 43.6 41.9 58.0
dónde se ha utilizado la siguiente transformación (para simplificar cálculos)
x1i =
Ti − 1525
75
y
x2i =
ti − 95
.
25
Estimar el modelo de regresión
yi = β 0 + β 1 x1i + β 2 x2i + β 3 x1i x2i + ui
e indicar qué parámetros son significativos para nivel de significación 0.05, teniendo en
cuenta que la desviación tı́pica residual es b
sR = 9.6. Estimar y contrastar el modelo anterior
empleando las variables originales Ti y ti .
64. Se ha ajustado un modelo de regresión para estudiar el efecto de la velocidad de corte (x1 )
y el caudal de refrigerante (x2 ) en la duración (y) de una herramienta de corte. Las tres
variables se han transformado mediante el logaritmo neperiano y el modelo estimado ha sido:
log y
= 18, 30 − 5, 050 log x1
(1,65)
(0,19)
− 3, 750 log x2
(0,34)
(entre paréntesis se proporcionan las desviaciones tı́picas estimadas de los coeficientes estimados del modelo). El número de observaciones es 32 y la desviación tı́pica residual b
sR = 0, 24.
Obtener los intervalos de confianza (99%) para los tres parámetros de la ecuación de regresión. El coeficiente de determinación es R2 = 0, 96, realizar el contraste conjunto de los
parámetros correspondientes a las dos variables explicativas.
65. Se ha ajustado el siguiente modelo de regresión múltiple con una muestra de 86 vehı́culos, de
los cuales 31 son japoneses , 41 norteamericanos y 14 europeos, dónde la variable dependiente
es el consumo, y los regresores: Pot (potencia) está expresada en unidades de 100 Cv, el
21
Peso en Toneladas, ZJ toma el valor 1 si el coche es japonés y cero en los demás, y ZE toma
el valor 1 para los coches europeos y cero en los demás.
yb = 3.305 + 0.843 Pot + 3.829

4.791e − 1
 5.054e − 2

(X T X)−1 = 
 −3.794e − 1
 −9.157e − 2
−4.682e − 2
Peso + 0.440 ZJ + 1.127 ZE
sb2R = 0.506,
5.054e − 2 −3.794e − 1 −9.157e − 2
1.595e − 1 −1.931e − 1 −3.443e − 3
−1.931e − 1
4.646e − 1
5.210e − 2
−3.443e − 3
5.210e − 2
6.667e − 2
−1.262e − 2
2.865e − 2
2.744e − 2
R2 = 75.7%

−4.682e − 2
−1.262e − 2 

2.865e − 2 

2.744e − 2 
9.759e − 2
Dar el intervalo de confianza para el consumo previsto de un coche norteamericano con una
potencia de 120 Cv y 1600 Kg de peso.
66. El modelo de regresión múltiple que relaciona el calor generado en el proceso de endurecimiento (variable dependiente) de 13 muestras de cemento en función de su composición
x1 , x2 , x3 y x4 , es
ybi =
62.4 + 1.55 x1i + 0.51 x2i + 0.10 x3i − 0.14 x4i
(70.1)
(0.74)
(0.72)
(0.75)
(0.71)
(entre paréntesis la desviación tı́pica estimada de las estimaciones de los parámetros). Abajo
se proporciona el coeficiente de determinación R2 de los 15 modelos de regresión diferentes
que se obtienen según los regresores elegidos.
R2
Variables en el Modelo
53.3948
x1
66.6268
x2
28.5873
x3
67.4542
x4
97.8678
x1 , x2
54.8167
x1 , x3
97.2471
x1 , x4
84.7025
x2 , x3
68.0060
x2 , x4
93.5290
x3 , x4
98.2285
x1 , x2 , x3
98.2335
x1 , x2 , x4
98.1281
x1 , x3 , x4
97.2820
x2 , x3 , x4
98.2376
x1 , x2 , x3 , x4
¿Qué variables influyen significativamente en el calor generado? Justificar la respuesta. ¿Qué
modelo seleccionarı́as para predecir el calor generado?
67. Se desea estudiar la relación entre el sueldo de 100 personas, en función del número de
años que llevan trabajando y el sector al que pertenecen, pudiéndose dividir el sector en
22
S=servicios, I=industria, A=agricultura. Escribir el modelo de regresión entre el sueldo
(variable respuesta) y el resto de las variables. Se estima este modelo de regresión obteniendo
una varianza residual sb2R = 0.25. Con el objetivo de contrastar si el sector influye en el sueldo
se estima otro modelo de regresión que no contiene ninguna variable de sector, para este
′
modelo se obtiene una varianza residual b
sR2 = 0.4. Contrastar si el sector influye en el sueldo
que perciben los empleados (α = 0.05).
68. En un modelo de regresión múltiple Y = Xβ+U se realiza la transformación de los regresores
Z = XA, donde X es la matriz de los regresores, y A una matriz cuadrada de rango máximo.
Calcular la estimación de los coeficientes del nuevo modelo Y = Zβ N + U en función de los
antiguos.
10.64. (S-00) Se ha estimado el siguiente modelo de regresión entre la variable y y los regresores
x1 , x2 y x3 ,
ŷ = 61.1 + 46.1 log x1 + 83.1 log x2 + 27.9 log x3 ,
ŝR = 5.49
Teniendo en cuenta que el número de observaciones es

0.1939 −0.0892

−0.0892 0.1924
(X T X)−1 = 
 −0.0887 −0.0125
−0.1534 0.0010
n = 60 y que

−0.0887 −0.1534
−0.0125 0.0010 

0.2093 −0.0066 
−0.0066 0.2613
Dar un intervalo de confianza para los 4 parámetros de la ecuación de regresión y para la varianza
del modelo (α = 0.05).
69. Se ha estimado un modelo de regresión múltiple para explicar el consumo de combustible
de automóviles en función del peso, la potencia y el lugar de fabricación. La muestra es de
86 vehı́culos, de los cuales 31 son japoneses (J), 41 norteamericanos (N) y 14 europeos (E).
yb = 3.305 + 0.843 Pot + 3.829 Peso + 0.440 ZJ + 1.127 ZE ,
sb2R = 0.506, R2 = 75.7%


4.791e − 1
5.054e − 2 −3.794e − 1 −9.157e − 2 −4.682e − 2
 5.054e − 2
1.595e − 1 −1.931e − 1 −3.443e − 3 −1.262e − 2 


T
−1

−3.794e
−
1
−1.931e
−
1
4.646e
−
1
5.210e
−
2
2.865e
−
2
(X X) = 


 −9.157e − 2 −3.443e − 3
5.210e − 2
6.667e − 2
2.744e − 2 
−4.682e − 2 −1.262e − 2
2.865e − 2
2.744e − 2
9.759e − 2
La variable dependiente, el consumo, está medida en litros cada 100 km, Pot es la potencia
y está expresada en unidades de 100 Cv, el Peso en Toneladas, ZJ toma el valor 1 si el coche
es japonés y cero en los demás, y ZE toma el valor 1 para los coches europeos y cero en
los demás. Realizar el contraste general de regresión y los contrastes individuales para el
modelo anterior. Interpretar el resultado.
70. En una muestra de 31 árboles se ha medido la altura (x1i ), el diámetro del árbol a un metro
de altura sobre el suelo (x2i ) y el volumen de madera del tronco (yi ) y se ha estimado el
siguiente modelo de regresión
log(yi ) = β 0 + β 1 log(x1i ) + β 2 log(x2i ) + ui .
Los resultados se muestran en las tablas siguientes:
23
Análisis de regresión múltiple
Variable dependiente: Log(Volumen)
Regresor
Estimación Desviación tı́pica Estadı́stico t Nivel crı́tico
Ordenada en el origen
-6,63162
0,79979
-8,2917
0,0
Log(Altura)
1,11712
0,20444
-5,4644
0,0
Log(Diámetro)
1,98265
0,07501
26,4316
0,0
Fuente
Modelo
Residual
Total
Análisis de la varianza
Suma de cuadrados G. de L. Varianzas Cociente F Nivel crı́tico
8,12323
2
4,06161
613,19
0,0
0,18546
28
0,00662
8,30869
30
Aproximando el volumen del árbol por el de un tronco cónico, el volumen debe ser proporcional
a kx1i x22i y tomando logaritmos
log(k) + log(x1i ) + 2 log(x2i ).
Realizar los siguientes contrastes de hipótesis con nivel de significación 0,05:
′
H0 : β 1 = 1
H0 : β 2 = 2
.
H1 : β 1 6= 1
H1′ : β 2 6= 2
71. Una medida crı́tica de calidad en la fundición de llantas de aluminio por inyección es la
porosidad. Se ha realizado un diseño 22 replicado (n = 16 experimentos) para analizar la
porosidad (Y ) en función de la temperatura (T ) del aluminio lı́quido y de la presión (P ) con
que éste se inyecta al molde. El modelo obtenido ha sido
ŷ
= 2.84 +
0.59 T
- 0.031 P
- 0.22 T P
y ŝR = 0.137 . Indica qué efectos son significativos (α = 0.05) y las condiciones óptimas de
fabricación
72. En la tabla siguiente se presenta la estimación de la regresión entre el resultado en la prueba
del salto de longitud de 34 atletas y los tiempos de estos mismos atletas en las pruebas de
100 metros lisos, 110 metros valla, 400 metros y 1500 metros.
Constante
X1 (100 m)
X2 (110 m)
X3 (400 m)
X4 (1500 m)
Coeficientes
b
β
Desv. T.
i
17.9
2.12
-.462
.266
-.181
.124
-3.39E-02
.070
-4.47E-03
.004
t
p-valor
8.45
0.000
-1.73
0.093
-1.45
0.155
-.485
0.631
-1.03
0.312
La variabilidad total de los datos es 4.613, la variabilidad explicada 2.199 y la variabilidad
residual 2.413. Realizar el contraste general de regresión, e interpretar el resultado del
contraste y los contrastes individuales de la tabla.
24