Curvas paramétricas

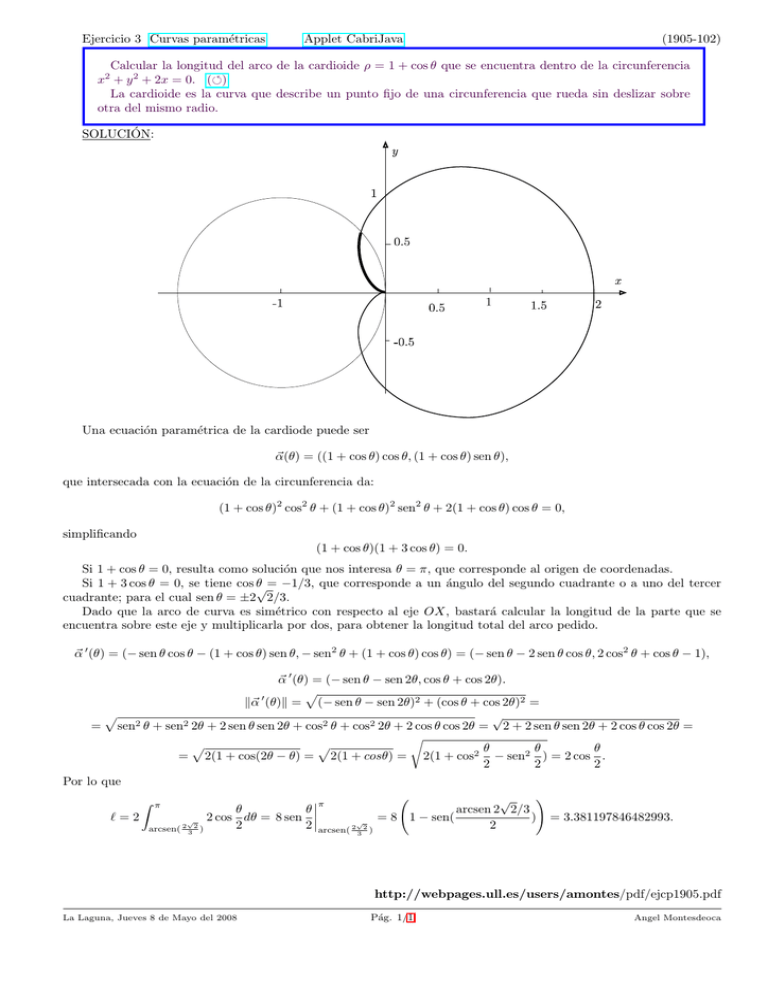
Ejercicio 3 Curvas paramétricas
Applet CabriJava
(1905-102)
Calcular la longitud del arco de la cardioide ρ = 1 + cos θ que se encuentra dentro de la circunferencia
x2 + y 2 + 2x = 0. (ª)
La cardioide es la curva que describe un punto fijo de una circunferencia que rueda sin deslizar sobre
otra del mismo radio.
SOLUCIÓN:
Una ecuación paramétrica de la cardiode puede ser
α
~ (θ) = ((1 + cos θ) cos θ, (1 + cos θ) sen θ),
que intersecada con la ecuación de la circunferencia da:
(1 + cos θ)2 cos2 θ + (1 + cos θ)2 sen2 θ + 2(1 + cos θ) cos θ = 0,
simplificando
(1 + cos θ)(1 + 3 cos θ) = 0.
Si 1 + cos θ = 0, resulta como solución que nos interesa θ = π, que corresponde al origen de coordenadas.
Si 1 + 3 cos θ = 0, se tiene cos θ√= −1/3, que corresponde a un ángulo del segundo cuadrante o a uno del tercer
cuadrante; para el cual sen θ = ±2 2/3.
Dado que la arco de curva es simétrico con respecto al eje OX, bastará calcular la longitud de la parte que se
encuentra sobre este eje y multiplicarla por dos, para obtener la longitud total del arco pedido.
α
~ 0 (θ) = (− sen θ cos θ − (1 + cos θ) sen θ, − sen2 θ + (1 + cos θ) cos θ) = (− sen θ − 2 sen θ cos θ, 2 cos2 θ + cos θ − 1),
α
~ 0 (θ) = (− sen θ − sen 2θ, cos θ + cos 2θ).
p
k~
α 0 (θ)k = (− sen θ − sen 2θ)2 + (cos θ + cos 2θ)2 =
p
√
= sen2 θ + sen2 2θ + 2 sen θ sen 2θ + cos2 θ + cos2 2θ + 2 cos θ cos 2θ = 2 + 2 sen θ sen 2θ + 2 cos θ cos 2θ =
r
p
p
θ
θ
θ
= 2(1 + cos(2θ − θ) = 2(1 + cosθ) = 2(1 + cos2 − sen2 ) = 2 cos .
2
2
2
Por lo que
Ã
!
√
¯π
Z π
θ
θ ¯¯
arcsen 2 2/3
`=2
2 cos dθ = 8 sen ¯
= 8 1 − sen(
) = 3.381197846482993.
√
2
2 arcsen( 2√2 )
2
arcsen( 2 3 2 )
3
http://webpages.ull.es/users/amontes/pdf/ejcp1905.pdf
La Laguna, Jueves 8 de Mayo del 2008
Pág. 1/1
Angel Montesdeoca