Ejemplos - Facultad de Ciencias Matemáticas

AMPLIACIÓN DE MATEMÁTICAS
EJEMPLOS DE OTRAS SERIES DE FOURIER
Ejemplos 1.
1. La familia {1, cos nx, sen nx}n sobre el intervalo
[−π, π] (o sobre cualquier intervalo de longitud 2π, [a, a + 2π])
es un caso particular de familia ortogonal sobre la que ya sabemos
como calcular los coeficientes de Fourier y la serie de Fourier de
una función dada. Y estos no son más que un caso particular de
la definición anterior.
2. La familia {1, cosnx}n sobre el intervalo [0, π] es una familia
ortogonal, como ya sabemos. En el ejemplo que sigue veremos
como calcular la serie de Fourier de una función respecto de esta
familia. Ello no será sino otro caso particular de la definición
anterior.
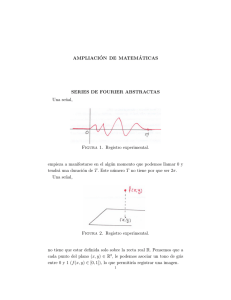
Ejemplo 1. Se considera la función f (x) = x(π−x), x ∈ [0, π]. Vamos
a calcular una serie de Fourier de esta función.
Figura 1. f y su extensión.
La gráfica de f en el intervalo [0, π] es un arco de parábola y podemos extender esta función de forma π-periódica como se muestra en
1
2
C. RUIZ
el dibujo. Como es π-periódica en particular también es 2π-periódica y podrı́amos calcular su serie de Fourier respecto de la familia
{1, cos nx, sen nx}n sobre el intervalo [−π, π] (en este caso observemos
que la función serı́a par y por tanto los coeficientes bn serı́an nulos).
No vamos a hacerlo. Vamos a calcular otra serie de Fourier, la asociada a la familia {1, cosnx}n sobre el intervalo [0, π]. Siguiendo la
definición previa, ahora los coeficientes de Fourier son:
Rπ
2
Z π
3 f
(x)dx
1
x
π
x
1
π
0R
=
−
x(π − x)dx =
a0 =
π 2
π 0
π 2
3 0
1 dx
0
3
1 π
π3
π2
3π 2 2π 2
=
−
−
= .
=
π 2
3
6
6
6
y
Rπ
f (x) cos nxdx
para
n ≥ 1.
an = 0 R π
cos2 nxdx
0
Z π
Z
1 π
π
2
cos nx =
cos2 nxdx = . Luego
Recordemos que
2 −π
2
0
Z π
Z π
2
2
an =
πx cos nxdx −
x2 cos nxdx.
π 0
π 0
Las dos integrales anteriores se resuelven por partes.
Z
π
0
Z
luego
Z π
sen nx
x sen nx π
x cos nxdx =
−
dx
0
n
n
0
−1 − cos nx π
1
=
=
[cos nπ − 1],
0
n
n
n2
π
x cos nxdx =
0
−2
si n es impar y cero en otro caso.
n2
La otra integral
Z
0
π
Z
x2 sen nx π
2 π
x cos nxdx =
x sen nxdx
0 −n
n
0
Z π
2 x cos nx π
(−1)n 2π
cos nx
=
−
dx
=
.
0
n
n
n
n2
0
2
Ası́ si n = 2k es par,
n
=
−2 (−1)n 2π
1
= − 2.
2
π
n
k
APUNTES AM
3
Por otro lado si n = 2k + 1 es impar,
an = −
4
−2 (−1)2k+1 2π
+
=0
(2k + 1)2
π (2k + 1)2
y por tanto la serie de Fourier de la función f (x) = x(π − x) respecto
de la familia ortogonal {cos nx}, con x ∈ [0, 1], es
∞
π2 X 1
−
cos 2kx.
6
k2
k=1
1 si 0 ≤ t ≤ π
−1 si −π ≤ t < 0.
Ejemplo 2. Consideremos la función f (t) =
Figura 2. Función escalón.
La serie de Fourier de la función f asociada a la familia ortogonal
{e }n∈Z vendrá dada por unos coeficientes de Fourier
Rπ
f (t)eint dt
−π
R
an = π int 2
para
n ∈ Z.
|e | dt
−π
Z π
Ahora como
|eint |2 dt = 2π y
int
−π
Z
π
Z
0
=
−int
Z
π
−e−int dt
−π
−π
0
−int −int e
e
0
π
=
+
−π
in
−in 0
1
1
2
2
= [cos(−0n) − cos(nπ)] +
[cos(−nπ) − cos(0n)] =
−
cos nπ.
in
−in
in in
f (t)eint dt
−e
dt +
4
C. RUIZ
2
Ası́ an =
si n es impar y nulo en otro caso. La serie de Fourier de
inπ
f en esta situación será
∞
∞
X
X
−2i
2
i(2k+1)t
e
=
ei(2k+1)t .
i(2k
+
1)π
(2k
+
1)π
k=−∞
k=−∞
Observación 1. La forma compleja de la serie de Fourier permite
ver más claramente la relación existente entre la serie de Fourier y
la transformada de Fourier, la otra gran herramienta del Análisis de
Fourier.
Referencias
Departamento de Análisis Matemático, Facultad de Matemáticas,
Universidad Complutense, 28040 Madrid, Spain
E-mail address: Cesar [email protected]