Enunciados
Anuncio

AMPLIACIÓN DE CÁLCULO
Práctica 1
Integración Múltiple
Curso 2013-2014
1. Sea R la región del plano interior a la circunferencia de radio 1 y centro (0,1) limitada inferiormente por la recta y = 2 − x.
a) ¿Se trata de una región regular? En caso afirmativo escribirla como una región regular en
ambas direcciones.
∫∫
b) Comprobar que se cumple el teorema de Fubini para
x dx dy.
R
∫∫
x2 dx dy donde R es la región plana limitada por la curva r = 4 cos θ e indicar cómo
2. Evaluar
R
se plantearı́a en coordenadas cartesianas.
3. Calcular el área de la región plana limitada por y = 4x − x2 , y = −3x + 6 y el eje OX.
4. Una pirámide está limitada por los tres planos coordenados y el plano x + 2y + z = 2.
a) Calcular su volumen.
b) Hallar su centro de masa si su densidad es constante.
5. Hallar la masa de la cardioide r = 1 + sen θ si la densidad en cada punto (r, θ) es d(r, θ) = r.
6. Se considera la lámina plana dada por:
{
}
b
R = (x, y) ∈ R2 : x2 ≤ y ≤ ax2 , y ≤
x
siendo a = 11−última cifra de tu dni, b = 2+ penúltima cifra de tu dni.
a) Calcular el área de la lámina.
b) Hallar el momento de inercia de la lámina respecto al eje Y teniendo en cuenta que la
1
.
densidad viene dada por: d(x, y) =
(y − ab)2
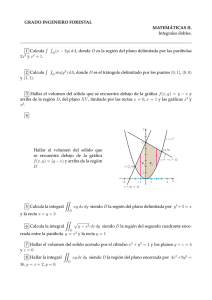
7. Hallar el área de la porción de la superficie z = y 2 + 4x situada sobre la región triangular del
plano XY cuyos vértices están en (0, 0), (0, 2) y (2, 2).
∫∫∫
(x2 + y 2 + z 2 ) dx dy dz siendo R la región bajo el cono z =
8. Calcular
√
x2 + y 2 , sobre el
R
plano OXY , e interior a la esfera x2 + y 2 + z 2 = 1. ¿Cuáles son las coordenadas que facilitan
más el cálculo?
∫∫∫
√
x2 + y 2 dx dy dz en el caso en el que R es la región del octante positivo situada
R
(
)
1 2
1
2
2
bajo el paraboloide z = x + y e interior al cilindro x −
+ y2 = .
2
4
9. Hallar
zy
10. Hallar el volumen del sólido acotado por las gráficas del cono z =
cilindro x2 + y 2 = 25, usando una integral triple.
√
x2 + y 2 , el plano z = 0 y el
11. Calcular la masa del sólido comprendido entre las esferas de radio 1 y 5 centradas en el origen
cuya densidad en cada punto es inversamente proporcional a la distancia del punto al origen.
12. Hallar el momento de inercia respecto del eje OZ del sólido comprendido entre el paraboloide
hiperbólico z = 9 + x2 − y 2 , el plano z = 0 y el cilindro x2 + y 2 = 9 en el octante positivo, cuya
densidad en cada punto es proporcional a la distancia de dicho punto al plano y = 0. Comprobar
que se obtiene el mismo resultado empleando coordenadas cartesianas y cilı́ndricas.
13. Calcular el volumen exterior al paraboloide elı́ptico x2 + y 2 = z e interior al hiperboloide de una
hoja x2 + y 2 − z 2 = 1, entre los planos z = 0 y z = 5.
14. Se desea calcular el volumen comprendido entre los conos z 2 = x2 + y 2 , 2z 2 = x2 + y 2 y la esfera
x2 + y 2 + z 2 = 1 en el octante positivo.
a) Escribir la(s) integral(es) triple(s) necesaria(s) para calcular dicho volumen empleando coordenadas cilı́ndricas y esféricas.
b) Obtener el volumen de una de las dos formas planteadas.
Problemas para entregar el 23 de septiembre:
Todos/as los estudiantes deben entregar el problema número 6 y además
c
Problemas
siendo c la última cifra de tu dni.
0
11
1
1
2
2
3
14
4
4
5
13
6
12
7
7
8
8
9
9