Solución Problemas

ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE TELECOMUNICACIÓN
UNIVERSIDAD POLITÉCNICA DE VALENCIA
ANTENAS
22 de abril de 2009
Problema 1
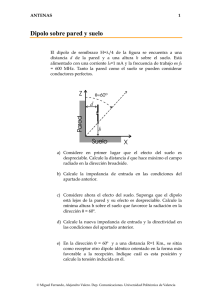
Una agrupación está formada por tres dipolos de brazo H = λ/4 colineales alimentados en paralelo, tal y
como se muestra en la figura. La distancia de separación entre los dipolos es d = 0, 75 λ. La impedancia de
entrada de cada dipolo aislado es de 75 + j43 Ω.
Suponga de momento que los dipolos están desacoplados y que la corriente a la entrada de todos ellos es la
misma (I1 = I2 = I3 ).
a) Calcule el campo radiado por la antena. (2 puntos)
b) Represente los cortes en plano E y en plano H del diagrama de radiación de la antena. (2 puntos)
c) Calcule la directividad de la antena. (2 puntos)
Impedancia mútua entre dipolos colineales H = λ/4
30
I1
25
d
Iin
I2
Re{z21 }
Im{z21 }
20
15
10
H
I3
5
0
-5
-10
0.5
0.75
1
d/λ
1.25
1.5
Considere ahora el acoplo entre los diplos, valiéndose de la gráfica de la impedancia mútua de dos dipolos
colineales con H = λ/4.
d) Calcule el cociente I2 /I1 e I3 /I1 . (2 puntos)
e) Obtenga una expresión para el nuevo factor de agrupación y comente brevemente cómo cree que se modificará el diagrama de radiación con respecto al caso en que no habı́a acoplo entre los dipolos. (2 puntos)
Problema 2
Considere un diagrama de campo de tipo omnidirecional en un plano y sectorial en cualquier plano ortogonal
al omnidireccional. Tal diagrama se expresa como
(
∆θc
π
c
1, π2 − ∆θ
2 ≤θ ≤ 2 + 2
d (θ) =
0, resto
a) Obtenga la expresión de la directividad en función de ∆θc . Aproxime la expresión obtenida por otra más
sencilla válida para ∆θc pequeños (2 puntos)
b) Se desea sintetizar un diagrama sectorial parecido al anterior y para ello se utiliza un hilo de corriente de
2π
2π
longitud L. La distribución de corriente por el hilo es de la forma I (z) = 1+ej L z +e−j L z . Obtenga las transformada F (u) de cada uno de los tres términos de la distribución de corriente por separado. Represéntelos
gráficamente en función de u. NOTA: No tome módulo al hacer dicha representación. (2 puntos)
c) Obtenga la transformada suma de las tres anteriores. Represéntela gráficamente de forma aproximada en
función de u. No tome módulo. Obtenga una expresión para el ∆θc del diagrama sintetizado en función de
L.(2 puntos)
d) Obtenga el ancho de haz ∆θc cuando L = 20λ. Dibuje el diagrama de radiación. Determine la directividad
aproximadamente. (2 puntos)
e) Calcule la longitud efectiva máxima de la distribución de corriente asumiendo que el punto de alimentación
del hilo está en el centro del hilo, z = 0. (2 puntos)
Solución al Problema 1
a) El campo radiado por la antena será el producto del campo radiado por un dipolo de brazo H = λ/4 por el
factor de agrupación de una agrupación uniforme broadside:
~ =E
~ H=λ/4 · F A
E
Tomaremos como referencia la corriente de la antena central (I2 ), supondremos que los dipolos están alineados
con el eje z, y que la antena central está en el origen de coordenadas. De esta forma:
I2 −jkr cos π2 cos θ
= j60 e
θ̂
r sin θ
sin 3Ψ2 z
F A(Ψz ) =
sin ψ2z
~ H=λ/4
E
Ψz
= kz d =
2π
0, 75λ cos θ = 1, 5π cos θ
λ
Finalmente:
π
~ = j60 I2 cos 2 cos θ sin
E
r
sin θ
sin
9π
4
3π
4
cos θ −jkr
e
θ̂
cos θ
b) Suponiendo que los dipolos están alineados en el eje z, tanto el diagrama del dipolo como el de la agrupación
son omnidireccionales en el plano XY , y el campo eléctrico en ese plano está polarizado según ẑ. Por tanto
el plano E es cualquier plano en el que ϕ sea constante (por ejemplo el plano XZ o el Y Z), y el plano H es
el plano XY .
Primero obtendremos el diagrama del la agrupación, sabiendo que se trata de una agrupación uniforme de
N = 3 elementos con α = 0 y d = 0, 75λ. Es decir, que Ψz = 1, 5π cos θ. En la figura 1 se muestra la obtención
de dicho diagrama mediante el método gráfico.
|F A(Ψz )|
−4π
−3π
−π − 2π
-2π
3
α − kd
θ=π
0
α
2π
3
π
2π
3π
Ψz = kd cos θ + α
4π
α + kd
θ=0
z
Figura 1: Obtención del diagrama de la agrupación mediante el método gráfico
El diagrama total será el producto de los diagramas del dipolo y el de la agrupación, como se muestra en la
figura 1.
Agrupación
z
Producto
z
y
y
y
Plano H
Plano E
Dipolo H = λ/4
z
x
x
x
Tabla 1: Cortes plano E y plano H del diagrama de la antena
c)
D=
~ 2max 4πr2
|E|
η
Wr
~ max = |E|
~ λ/4,max · |F A|max = 60 |I2 | 3
|E|
r
Wr =
2
X
Re{Zin }|Iin |2 = 3 · 73 · |I2 |2
n=0
D=
602 |I2 |2 32 1
4πr2
= 4, 9 = 6, 9 dB
r2
120π 3 · 73|I2 |2
d) La relación entre tensiones y corrientes en los tres dipolos la proporcionan los parámetros de impedancias,
de tal forma que podemos escribir:
V1
= Z11 I1 + Z12 I2 + Z13 I3
V2
= Z21 I1 + Z22 I2 + Z23 I3
V2
= Z31 I1 + Z32 I2 + Z33 I3
Como los tres dipolos están en alimentados en paralelo, las tensiones de alimentación son iguales (V1 = V2 =
V3 ). Por otro lado los tres dipolos son idénticos y por tanto su autoimpendacia es la misma (Z11 = Z22 = Z33 ).
Además la influencia mútua entre el primer y el segundo dipolo es la misma que entre el segundo y el tercero,
ya que están separados la misma distancia (Z12 = Z23 ). Finalmente, sabemos por el teorema de reciprocidad
que Z21 = Z12 y Z31 = Z13 . Con todos estos datos podemos reescribir el sistema de ecuaciones anterior de
la siguiente forma:
V1
=
Z11 I1 + Z12 I2 + Z13 I3
(1)
V1
=
Z12 I1 + Z11 I2 + Z12 I3 = Z12 (I1 + I3 ) + Z11 I2
(2)
V1
=
Z13 I1 + Z12 I2 + Z11 I3
(3)
Igualando los dos valores de V1 de las ecuaciones (1) y (3) obtenemos:
V1 = Z11 I1 + Z12 I2 + Z13 I3 = Z13 I1 + Z12 I2 + Z11 I3
Z11 I1 + Z13 I3 = Z13 I1 + Z11 I3
(Z11 − Z13 ) I1 = (Z11 − Z13 ) I3
I3 = I1 →
I3
=1
I1
Igualando ahora los dos valores de V1 en las ecuaciones (1) y (2) y sustituyendo I3 = I1 se obtiene:
V1 = (Z11 + Z13 ) I1 + Z12 I2 = 2 Z12 I1 + Z11 I2
(Z12 − Z11 ) I2 = (2 Z12 − Z11 − Z13 ) I1
2 Z12 − Z11 − Z13
I2
=
I1
Z12 − Z11
Mirando en la gráfica de las impedancias mútuas de dipolos colineales de H = λ/4 para separaciones de
d/λ = 0, 75 y d/λ = 1, 5 podemos determinar el valor de Z12 y Z13 respectivamente:
Z12
=
2 − j 8Ω
Z13
=
2Ω
Por otro lado sabemos que Z11 = 73 + j43 Ω. Con todo ello:
2 Z12 − Z11 − Z13
71 + j59
I2
= 1, 06 ej0,07
=
=
I1
Z12 − Z11
71 + j51
e) Antes el factor de agrupación era:
F A(Ψz ) =
3Ψz
2
sin ψ2z
sin
O también:
F A(Ψz ) = e−jΨz + 1 + ejΨz = 1 + 2 cos(Ψz )
dado que todas las corrientes eran iguales. Ahora el nuevo factor de agrupación será (recordemos que hemos
tomado I2 como corriente de referencia):
I1 −jΨz I2
I3 jΨz
e
+
+
e
I2
I2
I2
1
1
F A(Ψz ) =
e−jΨz + 1 +
ejΨz
j0,07
1, 06 e
1, 06 ej0,07
F A(Ψz ) =
F A(Ψz ) = 0, 94 e−j0,07 e−jΨz + 1 + 0, 94 e−j0,07 ejΨz
F A(Ψz ) = 0, 94 e−j0,07 + 2 cos(Ψz )
donde Ψz = 1, 5π cos θ.
El efecto del acoplo sobre el diagrama de radiación será muy débil ya que la nueva distribución es casi
idéntica a la anterior. No obstante se aprecia que la distribución ya no es totalmente uniforme (lo cuál
ensanchará ligeramente el lóbulo principal y disminuirá ligeramente el NLPS), y por otro lado aparece
un ligero error de fase no lineal que al igual que en el caso de las bocinas producirá relleno de nulos,
ensanchamiento del lóbulo principal y disminuición del NLPS, pero todo en un grado muy ligero.
Solución al problema 2 a) La directividad de un diagrama dado se puede calcular mediante Dmax =
4π
2π π
∫ ∫ t (θ , φ ) sen θ dθ dφ
. En el caso particular que se plantea la expresión queda como 0 0
4π
Dmax =
=
π ∆θc
2π
2
+
∫
2
sen θ dθ
1
2
∆θ
sen c ∆θ c
2
π ∆θc
2
−
2
b) Las transformadas de cada uno de los términos que componen la corriente son para I1 ( z ) = 1 , F1 ( u ) = L
2π
z
L
para I 2 ( z ) = e
j
para I 3 ( z ) = e
−j
sen u
L
, siendo u = k z 2
u
, F2 ( u ) = L
2π
z
L
sen ( u + u ')
2π L
, siendo u ' =
⋅ =π u +u'
L 2
, F3 ( u ) = L
sen ( u − u ')
u −u'
1.2
Fsuma
1
F2 F1 F3
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-5
-4
-3
-2
-1
0
u/π
1
2
3
4
5
c) La figura anterior muestra la transformada suma de las tres calculadas en el apartado anterior. Como se puede ver, el lóbulo principal está entre −2π y 2π . Para obtener una expresión del ancho de haz entre ceros observamos que u = 2π = k
L
⎛ 2λ ⎞
cos θ c . Despejando θ c , θ c = cos −1 ⎜
⎟ . El ancho de haz entre ceros es 2
⎝ L ⎠
⎛π
⎞
∆θ c = 2 ⎜ − θ c ⎟ ⎝2
⎠
(
)
d) El diagrama de radiación es Fsuma u (θ ) ⋅ sen θ . Sin embargo, despreciaremos el término sen θ por tratarse de un diagrama muy directivo. La contribución de la transformada se obtiene a partir de Fsuma ( u ) usando el método gráfico. El margen visible, MV, es: ⎡ L L⎤
⎢⎣ −k 2 , k 2 ⎥⎦ = [ −20π , 20π ] 90
La gráfica muestra el diagrama polar normalizado. 1
60
120
0.8
Con la expresión obtenida en el apartado anterior obtenemos el ancho de haz entre ceros 0.6
30
150
0.4
∆θ c = 11.5º . 0.2
180
0
210
330
240
La directividad se puede obtener de forma aproximada a partir de la expresión deducida en a): Dmax =
2
= 10
∆θ c
300
270
e) La longitud efectiva máxima se calcula de forma sencilla mediante L
lef máx
L
2
1
1 2
⎛ 2π
=
=
I
z
dz
1 + 2 cos ⎜
(
)
∫
∫
I ( 0) −L
3 −L
⎝ L
2
2
L
⎞
z ⎟ dz = 3
⎠
(10 dB )