Document

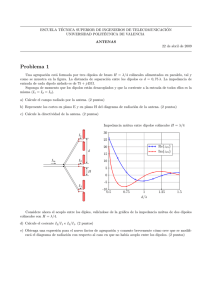
Cuadripolos cargados.
Funciones de Fase Mínima
El sistema se dice de fase mínima si tanto él como su
inversa son causales y estables.
Para todos los sistemas causales y estables que tienen la
misma respuesta en magnitud, aquellos de mínima fase
presentan el mínimo retardo.
En consecuencia la función transferencia de un sistema
que presenta sus ceros de transmisión en el eje jω o en el
semiplano izquierdo se dice función de Fase Mínima
En caso de que la función tenga uno o más ceros de
transmisión en el semiplano derecho se denomina función
de No Mínima Fase.
Cualquier función de transferencia de una red pasiva
recíproca en escalera es una función de mínima Fase.
Esto puede demostrarse:
1. Sea la red en escalera:
Los ceros de transmisión de dicha estructura se
logran con :
a) Los polos de las Z en serie
b) Los polos de la Y en paralelo.
2. Tanto las Z como las Y son funciones reales
positivas y por consiguiente no tienen polos en el
semiplano derecho.
3. Las funciones transferencia que caracterizan este
tipo de redes son Funciones de Fase Mínima
Determine si la función transferencia V2/V1 del siguiente
circuito es de Mínima Fase:
1
I1 ( s  )  V1
s
V1
I1 
1
(s  )
s
1
I 2 ( s  )  V1
s
V1
I2 
1
(s  )
s
I1  I 2
1
(s  )
1
1
s V
V2  I 2 s  I1  I1 ( s  ) 
1 1
s
s
(s  )
s
1
(s  )
V2
s2 1
s

 2
V1 ( s  1 ) s  1
s
Esta función que corresponde a una estructura
Puente o Lattice simétrica tiene polos complejos
conjugados sobre jω y un cero en s=+1 y otro cero en
s=-1.
Por lo tanto no es una función de Fase Mínima.
Se demuestra que la red lattice o puente sin carga se caracteriza
por las relaciones con los parámetros de cuadripolos:
Z a  Z11  Z12
Z b  Z11  Z12
G12 
V2
V1

I 2 0
Z b  Z a p(s)

Z b  Z a q(s)
Z a 1  G12 q ( s )  p ( s )


Z b 1  G12 q ( s )  p ( s )
Z a  1  G12
V2
Z b  1  G12
La realización será factible en la
medida en que Za y Zb sean FRP.
Para ello si es necesario se afecta
a G12 por una constante
k1G12  k1
p( s)
q( s)
Donde k1 puede ser lo suficientemente pequeña, así el 1 de
1±G12 es el que permite hacer los términos de las expansión en
fracciones parciales de Za positivos
Síntesis de Redes de Resistencia
Constante


Consideremos el caso de
cuadripolos pasivos que
presenten una resistencia R a
la entrada cuando a la salida
se les conecta una R del
mismo valor.
En este caso es factible
conectar en cascada, así la
función transferencia resulta:
Vo V2 V0
 x
Vi Vi V2
La función transferencia se puede descomponer en el
producto de relaciones de tensión más simples, que puedan
realizarse como redes de resistencia constante

Hay diferentes tipos de redes de resistencia
constante:
1. Redes puente o lattice.
2. Redes T-puenteadas.
Red Lattice simétrica:
Se demuestra que la matriz de parámetros Z o de circuito abierto
es:
 z11
z
 21
 z a  zb
z12   2


z22   za  zb
 2
z a  zb 
2 
z a  zb 

2 
Condición de simetría: Z11= Z22
Calculando la impedancia que presenta una red de dos puertos
pasiva y simétrica terminada en una resistencia R:
Las ecuaciones de red:
z11I1  z12 I 2  V1
z12 I1  ( z11  R) I 2  0
De donde:
I1 
( z11  R)V1
2
2
z11  z11R  z12
V z  z11R  z12
Z entrada  1  11
I1
z11  R
2
2
z  z11R  z12
R  11
z11  R
2
Si Zentrada debe ser igual a R
R  z11  z12
2
2
2
Reemplazando los parámetros por los correspondientes a la red
Lattice
 z a  zb   z a  zb 
R 
 

 2   2 
2
R  z a zb
2
Es la condición para que la red Lattice
presente R constante
Si la estructura es doblemente cargada, con resistencia de
generador Rg
Se demuestra que la función transferencia
es:
V2 1 Z b  R

Vg 2 Z b  R
V2 1 R  Z a

Vg 2 R  Z a
Estas son las
ecuaciones de
diseño de la red
Lattice simétrica
Esencialmente la red se sintetiza igualando coeficientes
Red T-puenteada de Resistencia
Constante
Otra configuración empleada en Redes de Resistencia Constante
es la red T-puenteada.
Analizando la red, para que cumpla con estas características se
demuestra que:
R 2  Z a Zb
En este caso:
Zb
V2
R


V1 R  Z a Z b  R
Predistorsión
En el diseño de Filtros pasivos
Se ha supuesto hasta el momento que los inductores y
capacitores no presentan pérdidas, por lo tanto no hay
disipación asociada.
 En realidad estos elementos presentan pérdidas, tanto el
inductor como el capacitor tienen resistencias asociadas. El
inductor tiene una R asociada a su bobinado y en el
capacitor el dieléctrico no es un aislante perfecto, por lo
tanto ambos tienen resistencia finita.

Factor de
calidad.
Medido a
una
frecuencia
de corte, o
frecuencia
central de
un filtro
X L L
qL 

RL
RL
RC
qC 
 CRC
XC
Para el inductor,
circuito serie
En el capacitor
circuito
equivalente
paralelo

Caso ideal
RL  0,
qL  
RC  , qC  
Valores prácticos qL = 15 o menor
qC=100
Z L  sL  RL  ( s 
ZC 
Normalizando en relación a ω0
Z L  (s 
ZC 
1
)L
qL
1

1
 s 
qC

0
qL
)L
1
1

sC  GC  0 
 s  C
qC 

En el proceso de denormalización
de frecuencia
s
s
0
el factor de denormalización completo

C

queda :
 0 
 s  
q 

0

Si definimos al factor de pérdidas como la inversa del factor de calidad:
1
dL 
qL
1
dC 
qC
así : Z L  ( s  d L ) L
ZC 
1
s  dc C


Como vemos hay un corrimiento de la frecuencia que tiene como
origen las pérdidas.
Si se supone pérdidas uniformes:
d d d
L
C
Con el fin de obtener realizaciones prácticas que consideren L y
C en condiciones reales se utilizará la predistorsión.
Proceso de Predistorsión en el diseño de un filtro,
como cuadripolo sin pérdidas terminado en una R
de carga
1.
2.
3.
Se reemplaza s por s-d en H(s) pues se conoce a priori que existirá un
corrimiento a posteriori de magnitud s+d, por lo tanto se tratará de
ecualizarlo.
Se realiza H’(s)=H(s-d) como una red LC terminada en un resistor.
Se remueve los efectos de la predistorsión reemplazando s por s+d, así
se añade una RL en serie con los inductores y una RC en paralelo con los
capacitores.
En este paso se está realizando una H’(s) cuyas singularidades tienen un
desplazamiento en la dirección de +σ. Con este corrimiento las
singularidades (polos y ceros) no deben salir del semiplano izquierdo del
plano complejo.
Ejemplo

Diseñar el filtro que presenta la siguiente
especificación con RL=1
V2
2
H ( s)   2
V1 s  2s  2
Considerando que qL=qC=4 y d=1/4
 Se reescribe H(s) como H’(s)=H(s-1/4) y se
sintetiza dicha expresión:

2
H '( s) 
3
25
2
s  s
2
16
1
V2
2
H ( s)   2
V1 s  2s  2
jw
0.5
0
Polos
-1 + j 1
-1 - j 1
-0.5
-1
-1
-0.5
0
Sigma
0.5
1
2
H '( s) 
3
25
s2  s 
2
16
Polos
-0.75 + j 1
-0.75 - j 1
Es un filtro pasabajos del tipo todo polos, por lo tanto
sintetizo con la primera forma de Cauer.
Diseñando con los valores predistorsionados el circuito con elementos ideales
presenta la siguiente estructura:
Considerando el diseño con los elementos con pérdidas se obtiene la
siguiente topología
24 1 6
*  
25 4 25
2 1 1
Gc  C * d  *  Mho
3 4 6
Rc  6
RL  L * d 

A partir del análisis se obtiene la siguiente H(s)
V2
25 /16
H ( s)   2
V1 s  2s  2

La especificación fue
V2
2
H ( s)   2
V1 s  2s  2

El diseño con elementos con qL= qC=4
V2
25 /16
H ( s)   2
V1 s  2s  2
1
Volvieron los polos a la ubicación
de la especificación
La diferencia que se obtiene es la
atenuación a frecuencia cero

[dB]  20log 25 / 32  2.1442dB
jw
0.5
0
-0.5
-1
-1
-0.5
0
Sigma
0.5
1