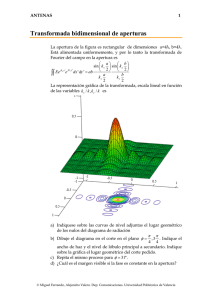
ω ω ω ω π ω = π ω = τ ω

UNIVERSIDAD DE
ALCALÁ
Escuela Politécnica
Ingeniería de
Telecomunicación
Nombre:
Apellidos:
Curso: 2º
Departamento de Teoría de
la Señal y Comunicaciones
Fecha: 23 - enero – 2006
Asignatura: Señales y Sistemas I
PROBLEMA 1.
3 Puntos
A la entrada del sistema de la figura1 se aplica la señal x(t ) = sinc (2t ) . Se desea
obtener:
1. La representación gráfica de X 1 (ω ), X 2 (ω ), X 3 (ω ) e Y (ω ) . Considerar para
este apartado que ω1 = 3π rad / s .
2. Calcular el valor de τ para que la salida del sistema sea nula si
ω1 = 3π rad / s .
3. Suponiendo que τ = 2 , calcular el menor valor que puede tomar ω1
( ω1 > 0 ) para que se cumpla que y (t ) = x1 (t ) .
Figura 1
siendo
Figura 2
T=
2π
ω1
RESULTADOS:
1.-
-
Y (ω ) = X 3 (ω ) ⋅ H 2 (ω )
2.- τ =
1
.
6
⎧ω1 = kπ
3.- ⎨
⎩ω1 ≥ 2π
⇒
k≥2
El menor valor será ω1 = 2π
1 Punto
Cuestión 1
Un sistema LTI causal tiene como función de transferencia H (s ) =
K
. Dicho
s ⋅ (s + 1)
sistema forma parte del diagrama de la figura 1.
Figura 1
1. Determinar el margen de valores de K (K real) que hacen que el sistema
total sea estable y que todos los polos de su función del sistema sean reales.
⎛ t + 2π ⎞
2. Determinar la salida del sistema total si la entrada es x(t ) = 5 ⋅ cos⎜
⎟.
⎝ 8 ⎠
1
(Suponga para este apartado que K = ).
8
RESULTADO
1.- 0 < K ≤
2.- y (t ) =
1
4
40
⎛t π
40
⎛ 8 ⎞⎞
⎛t π
⎞
⋅ cos⎜⎜ + − arctg ⎜ ⎟ ⎟⎟ =
⋅ cos⎜ + − 0.852 ⎟
113
113
⎝ 7 ⎠⎠
⎝8 4
⎠
⎝8 4
2 Puntos
Cuestión 2
El diagrama polo – cero de un sistema LTI estable es el de la figura 2.
Figura 2
Sabiendo que la respuesta impulsiva del sistema para n = 1 vale h [1] = −
7
:
20
1. Determinar la secuencia de entrada, x1 [n] , que hace que la salida sea
n
⎛1⎞
y1 [n] = ⎜ ⎟ ⋅ u[n] + 2 n ⋅ u[− n − 1] .
⎝ 3⎠
2. Determinar la secuencia de entrada, x2 [n] , que hace que la salida sea
n
⎛1⎞
y 2 [n] = ⎜ ⎟ ⋅ u[n] .
⎝ 3⎠
3. Determinar la respuesta impulsiva de los posibles sistemas inversos al dado.
RESULTADO:
1 −1
z
4
1.- H ( z ) = 3 ⋅
⎛ 1 −1 ⎞
−1
⎜1 − z ⎟ ⋅ 1 − 2 z
⎝ 3
⎠
1+
(
)
1
< z <2
3
5 ⎛ 1⎞
x1 [n] = − ⋅ ⎜ − ⎟
9 ⎝ 4⎠
n −1
⋅ u[n − 1]
n
n −1
⎤
1 ⎡⎛ 1 ⎞
⎛ 1⎞
⋅ u[n − 1]⎥
2.- x2 [n] = ⋅ ⎢⎜ − ⎟ ⋅ u[n] − 2 ⋅ ⎜ − ⎟
3 ⎢⎝ 4 ⎠
⎝ 4⎠
⎥⎦
⎣
n
8
⎛ 1⎞
x2 [n] = − ⋅ δ [n] + 3 ⋅ ⎜ − ⎟ ⋅ u[n]
3
⎝ 4⎠
3.- hI [n] =
n
8
68
65 ⎛ 1 ⎞
⋅ δ [n − 1] + ⋅ δ [n] − ⋅ ⎜ − ⎟ ⋅ u[n]
9
9
9 ⎝ 4⎠