Dipolo frente a suelo y pared

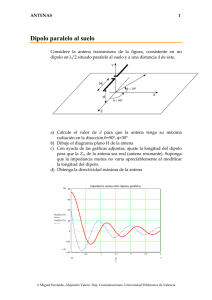
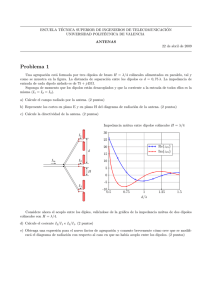
ANTENAS
1
Dipolo sobre pared y suelo
El dipolo de semibrazo H=λ/4 de la figura se encuentra a una
distancia d de la pared y a una altura h sobre el suelo. Está
alimentado con una corriente I0=1 mA y la frecuencia de trabajo es f0
= 600 MHz. Tanto la pared como el suelo se pueden considerar
conductores perfectos.
Z
θ=60º
Pared
d
h
Suelo
X
a) Considere en primer lugar que el efecto del suelo es
despreciable. Calcule la distancia d que hace máximo el campo
radiado en la dirección broadside.
b) Calcule la impedancia de entrada en las condiciones del
apartado anterior.
c) Considere ahora el efecto del suelo. Suponga que el dipolo
está lejos de la pared y su efecto es despreciable. Calcule la
mínima altura h sobre el suelo que favorece la radiación en la
dirección θ = 60º.
d) Calcule la nueva impedancia de entrada y la directividad en
las condiciones del apartado anterior.
e) En la dirección θ = 60º y a una distancia R=1 Km., se sitúa
como receptor otro dipolo idéntico orientado en la forma más
favorable a la recepción. Indique cuál es esta posición y
calcule la tensión inducida en él.
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
2
impedancia mutua entre dipolos paralelos
80
60
40
Re( Z( d , 0) )
Im( Z( d , 0) ) 20
0
20
40
0.5
1
1.5
2
2.5
3
d
λ
Imped. mutua entre dipolos colineales
40 40
30
Re( Z( 0 , d) ) 20
Im( Z( 0 , d) )
10
0
− 10
10
0.5
.5
1
1.5
2
d
λ
2.5
3
3
Nota: en la segunda gráfica d es la distancia entre los centros de los
dipolos
Solución
Campo máximo debido al plano de masa
Aplicando imágenes observamos que la radiación de un dipolo junto
a la pared es equivalente a la radiación de un conjunto de dos
dipolos separados una distancia 2d, con corrientes opuestas. El
campo producido por dos dipolos se calcula por superposición
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
3
G G jkrˆ dxˆ
jkrˆ dxˆ
E = E0 e ⋅( ) − e ⋅( − )
(
)
En la expresión anterior se ha supuesto que el origen de coordenadas
se encuentra entre los dipolos, en el punto donde antes se encontraba
el plano conductor.
La dirección broadside del dipolo se produce en θ=90º, φ=0º. En esa
dirección el campo es proporcional a
E ∝ sen(k x d ) = sen(kd )
Se observa que el campo es máximo cuando d=λ/4.
Impedancia de entrada
El dipolo imagen tiene una corriente igual y de sentido opuesto al
real. Planteando la interacción a partir de los parámetros impedancia
V1 = Z11 I1 + Z12 I 2
V2 = Z 21 I1 + Z 22 I 2
I 2 = − I1
La impedancia es Z in =
V1
= Z11 − Z12
I1
De las gráficas obtenemos
Z11 (d → 0) = 73 + j 42 Ω
Z12 (d = λ / 2) = −15 − j 30 Ω
Z in = 88 + j 72 Ω
Efecto del suelo
De forma similar al apartado a, ahora el campo se obtiene como
suma de un dipolo y su imagen. Ahora la imagen es colineal con el
dipolo y ambos poseen corrientes en el mismo sentido
⎛ ⎛ λ⎞ ⎞
jkrˆ⋅⎜ −⎜ h + ⎟ zˆ ⎟ ⎞
G G ⎛ jkrˆ⋅⎛⎜⎝ h + λ4 ⎞⎟⎠ zˆ
⎝ ⎝ 4⎠ ⎠
⎟
+e
E = E0 ⎜ e
⎜
⎟
⎝
⎠
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
4
Debemos obligar a que la interferencia entre el dipolo y su imagen
sea constructiva en la dirección θ=60º
e
⎛ λ⎞
jkrˆ⋅⎜ h + ⎟ zˆ
⎝ 4⎠
+e
⎛ ⎛ λ⎞ ⎞
jkrˆ⋅⎜ − ⎜ h + ⎟ zˆ ⎟
⎝ ⎝ 4⎠ ⎠
⎡ ⎛
λ⎞
⎤
= 2 cos ⎢ k ⎜ h + ⎟ cos θ ⎥
4⎠
⎣ ⎝
⎦
3
Se observa que el máximo se produce para h = λ
4
Impedancia de entrada
Por un procedimiento análogo al del apartado b), obtenemos la
impedancia como Z in = Z11 + Z12
Z11 (d → 0) = 73 + j 42 Ω
Z in = 73 + j 42 Ω
Z12 (d = 3λ / 2) 0
Dmáx = D(θ = 60º ) =
P(θ = 60º )
=
Wt / 4π r 2
1
120π
2
⎛ 1
2⎞
⎜ 60 2 I
⎟
3⎠
⎝ r
4π r 2 = 4.38 (6.4 dB )
73I 2
Señal recibida
La orientación más favorable para el dipolo receptor lo sitúa
perpendicular la la dirección de propagación considerada. De esta
forma el diagrama presenta un máximo.
Nótese que no hay desacoplo de polarización por lo que
Vca = lef máx ⋅ E (θ = 60º ) = 15 µV .
En donde como longitud efectiva se emplea la máxima que presenta
un dipolo de media onda. El valor de dicha longitud para un dipolo
G
λ
orientado en z es lef máx = zˆ
π
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia