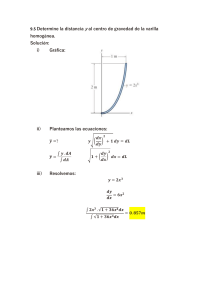
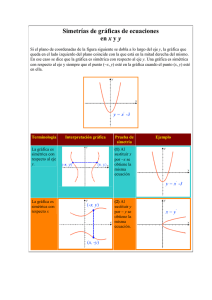
2 2 2 2 3 5 0 2 7 abcabc A ac

Encontrar los valores de a, b, y c para los cuales A es simétrica.
 2 a − 2b + 2c 2a + b + c 
5
A 3
a+c 


 0

7
−2
Ara que Asea simétrica:
A = AT
2
3
0


−2 
AT = a − 2b + 2c
5


 2a + b + c a + c 7 
Igualamos uno a uno los elementos de la matriz. Para formarlas ecuaciones.
2=2
3
a − 2b + 2c =
2a + b + c =
0
3
a − 2b + 2c =
5=5
a + c =−2
2a + b + c =
0
a + c =−2
7=7
Formamos las ecuaciones.
a − 2b + 2c = 3 − 2 f1 + f 2 → f 2
2a + b + c =
0
a + 0b + c =−2
Resolvemos por la eliminación de Gauss.
a − 2b + 2c =
3
0a + 5b − 3c =
−6
a + 0b + c =−2
a − 2b + 2=
c 3
0a + 5b − 3c =
−6
a + 0b + c =−2
− f1 + f3 → f3
a − 2b + 2c =
3
0a + 5b − 3c =
−6
0a + 2b − c =−5
a − 2b + 2c =
3
−6
0a + 5b − 3c =
− f1 + f3 → f3
0a + 2b − c =−5
a − 2b + 2c =
3
−6
0a + 5b − 3c =
Ahora el sistema está en triangular superior (U), o en forma escalonada.
1
13
−
0a + 0b + c =
5
5
Sin más resolvemos para c, luego b finalmente a. Todo esto en el sistema triangular (U).
1
13
c= −
5
5
c = −13
5b − 3c =
−6
5b − 3 ( −13) =
−6
5b + 39 =
−6
5b = −45
b = −9
a − 2b + 2c =
3
a − 2 ( −9 ) + 2 ( −13) =
3
a + 18 − 26 =
3
a= 3 + 8
a = 11
a = 11
b = −9
c = −13
En la Matriz A.
 2 a − 2b + 2c 2a + b + c 
A 3
a+c 
5


 0

−2
7
Con
a = 11
b = −9
c = −13
 2 11 − 2 ( −9 ) + 2 ( −13) 2 (11) + ( −9 ) + ( −13) 


A 3
5
11 + ( −13)

 0

−2
7
2 3 0 
=
A  3 5 −2 


 0 −2 7 
2 3 0 
AT ==  3 5 −2 


 0 −2 7 
A = AT
Entonces:
a = 11
b = −9
c = −13
Son la solución de la matriz A, para que sea simétrica.