Simetrías de gráficas de ecuaciones en x y y

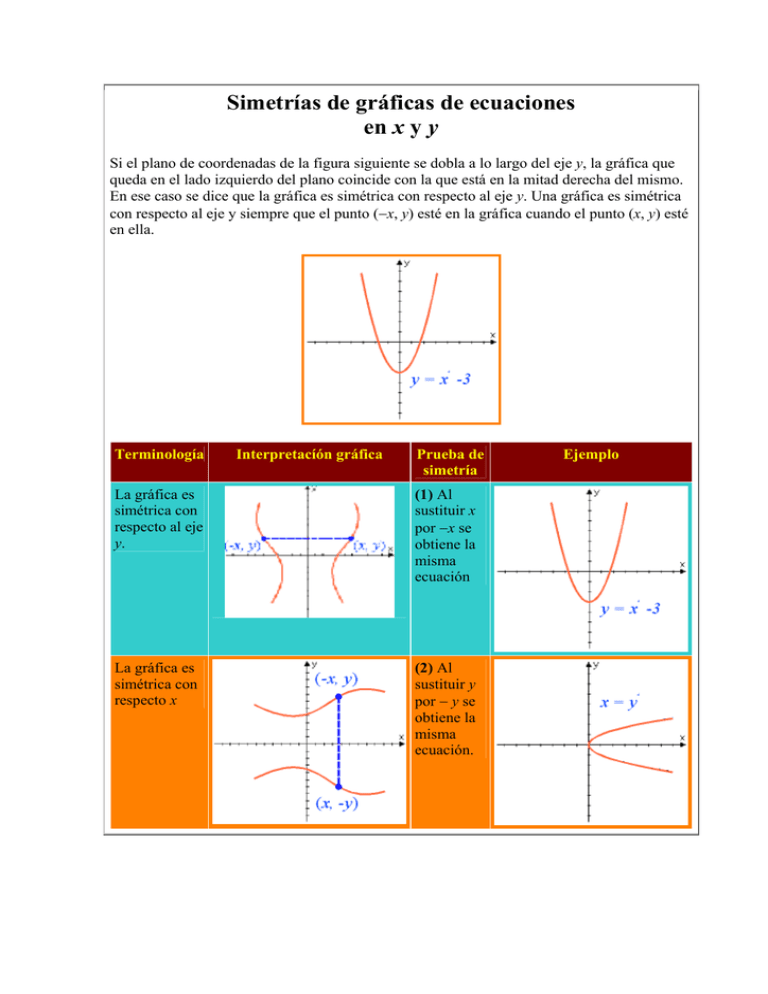
Simetrías de gráficas de ecuaciones
en x y y
Si el plano de coordenadas de la figura siguiente se dobla a lo largo del eje y, la gráfica que
queda en el lado izquierdo del plano coincide con la que está en la mitad derecha del mismo.
En ese caso se dice que la gráfica es simétrica con respecto al eje y. Una gráfica es simétrica
con respecto al eje y siempre que el punto (−x, y) esté en la gráfica cuando el punto (x, y) esté
en ella.
Terminología
Interpretacíón gráfica
Prueba de
simetría
La gráfica es
simétrica con
respecto al eje
y.
(1) Al
sustituir x
por −x se
obtiene la
misma
ecuación
La gráfica es
simétrica con
respecto x
(2) Al
sustituir y
por − y se
obtiene la
misma
ecuación.
Ejemplo
La gráfica es
simétrica con
respecto
(3) Al
sustituír x
por - x y y
por - y en
forma
simultánea,
se obtiene
la misma
ecuación.
Si una gráfica es simétrica con respecto a un eje, es suficiente determinarla en una mitad del
plano de coordenadas, ya que se puede hacer el esquema del resto mediante la imagen
especular, o reflexión, con respecto al eje que se trate.