Simetrías Funciones pares e impares
Anuncio
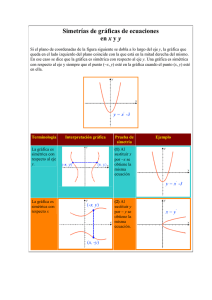
Simetrías En esta sección se estudian algunos medios auxiliares para trazar gráficas de determinados tipos de funciones. En particular el aspecto de la simetría de la gráfica de una función. Definición Se dice que una función es par si f(–x) = f(x) para toda x en su dominio. En este caso, la ecuación y = f(x) no cambia si se sustituye x por –x, y, por consiguiente, cuando esto sucede la gráfica de una función par es simétrica respecto al eje y. Se dice que una función f es impar, si f(–x) = –f(x) para toda x en su dominio. Para este caso la gráfica es simétrica con respecto al origen. Funciones pares e impares Trerminología Definición Ejemplo Simetría de la gráfica f es función par f(–x) = f(x) para toda x en el dominio y = f(x) = x2 eje y f es función inpar f(–x) = –f(x) para toda x y = f(x) = x3 el origen en el dominio