Tema 1: Funciones

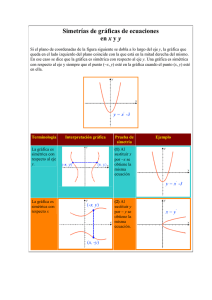
Tema 1: Funciones
Imagen con licencia Creative Commons tomada de Wikipedia
En este tema nos ocuparemos de introducir el
concepto de función y sus características
básicas.
Concepto de función
Una función es toda relación entre dos conjuntos de números
de forma que a cada elemento del primer conjunto le
corresponde un único elemento del segundo.
En toda función se relacionan dos tipos de elementos
numéricos. El primero se llama variable independiente, pues
toma cualquier valor sin depender de nadie. Suele
representarse por la letra x. El segundo recibe el nombre de
variable dependiente pues su valor depende del valor de x.
Suele representarse por la letra y.
Cuando un valor y depende del valor de x suele decirse que "y
es función de x" y se representa en la forma y = f(x) y los
valores que puede tomar la variable x se llama dominio de
definición.
Lo básico de una función
La variable independiente se llama discreta
cuando toma valores aislados, es decir,
entre un valor y el que le sigue no toma
valores intermedios.
La variable independiente se dice continua
cuando entre dos valores cualesquiera
siempre hay un valor intermedio.
Una función se dice que es continua si se
puede dibujar de un sólo trazo. Y se llama
discontinua en el caso contrario.
Elaboración propia
Crecimiento y decrecimiento, máximo y mínimo.
Una función se dice creciente si al
aumentar la variable independiente la
función se incrementa.
Es decreciente si al aumentar la variable
independiente la función disminuye.
Elaboración propia de las imágenes
Puntos de corte con los ejes
Los puntos donde una función corta al eje
de abscisas se obtienen igualando el valor
de la función a cero, es decir, son
aquellos que cumplen la ecuación f(x)=0.
El punto donde la gráfica corta al eje de
ordenadas se obtiene sustituyendo por
cero en la expresión analítica de la
función. Es decir, basta con hallar f(0).
Otras características
Una función f se dice periódica de periodo t si cumple que
f(x)=f(x+t), es decir, si se repite cada intervalo de longitud
t.
Una función f(x) se llama par o simétrica
respecto del eje vertical si dos valores de la
abscisa que se diferencien en el signo, tienen
la misma imagen. Es decir, f(-x)=f(x).
Una función f(x) se llama impar o simétrica
respecto del origen de coordenadas si dado un
punto cualquiera de la gráfica de la función, al
cambiarle el signo a la abscisa y la ordenada,
el punto obtenido también pertenece a la
gráfica de la función. Es decir, f(-x)=-f(x).
Formas de expresar una función
Mediante una frase o enunciado.
Mediante una tabla de valores.
Mediante una gráfica.
Mediante una expresión algebraica.
Elaboración propia