Sistema libre no amortiguado my// + ky = 0 Solución: y (t) = Acosω 0t

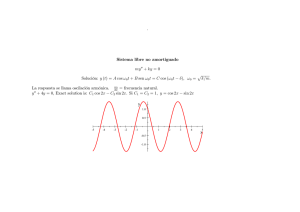
Sistema libre no amortiguado
my 00 + ky = 0
p
Solución: y (t) = A cos ω 0 t + B sen ω 0 t = C cos (ω0 t − δ), ω 0 = k/m.
La respuesta se llama oscilación armónica. ω2π0 = frecuencia natural.
y 00 + 4y = 0, Exact solution is: C1 cos 2x − C2 sin 2x. Si C1 = C2 = 1, y = cos 2x − sin 2x
y
1
0.5
0
-5
-2.5
0
2.5
5
x
-0.5
-1
1
Sistema libre amortiguado
my 00 + cy 0 + ky = 0
Ecuación característica: λ2 +
c
λ
m
+
k
m
c
= 0. Raíces: λ = − 2m
±
1
2m
√
c2 − 4mk
¾
1.- c2 > 4mk sobreamortiguado
no oscilan
2.- c2 = 4mk amortiguamiento crítico
3.- c2 < 4mk subamortiguado
√
1
En 1.- y 2.-, poniendo α = mc y β = 2m
c2 − 4mk (Luego β < α), resulta λ1 = − (α − β) , λ2 = − (α + β) .
Soluciones:
1.- y = c1 e−(α−β)t + c2 e−(α+β)t
2.- y = (c1 + c2 t) e−αt
En 3.- hemos puesto β = iω∗
3.- e−αt (A cos ω ∗ t + B sen ω ∗ t) = Ce−αt cos (ω ∗ t − δ)
√
1
con ω ∗ = 2m
4mk − c2 . Así, λ1 = − (α − iω ∗ ) , λ2 = − (α + iω ∗ )
1.- Sobreamortiguado
2.- amortig. crítico
2
3.- Subamortiguado
Oscilaciones forzadas
my 00 + cy 0 + ky = r (t)
La solución general se obtiene por superposición de la solución yh del sistema homogéneo (libre) con una solución particular yp . Si
r (t) = F0 cos ωt, onda de entrada de frecuencia ω/2π, se puede calcular yp por el método de coeficientes indeterminados. Si la
frecuencia de entrada ω/2π no coincide con la frecuencia natural del sistema, ω0 /2π, con ω 20 = k/m, resulta k − mω 2 6= 0 y
entonces
yp = a cos ωt + b sen ωt,
con a = F0
k − mω 2
ωc
, b = F0
2
(k − mω 2 ) + ω2 c2
(k − mω 2 )2 + ω 2 c2
Caso no amortiguado: c = 0.
yp =
F0
F0
cos
ωt
=
m (ω 20 − ω2 )
k
1−
y (t) = yh + yp = C cos (ω 0 t − δ) +
1
³ ´2 cos ωt.
ω
ω0
F0
cos ωt,
m (ω 20 − ω 2 )
suma de dos ondas:
una con frecuencia natural y otra con la frecuencia de entrada. La amplitud máxima de la solución particular es
·
³ ´2 ¸−1
F0
ρ, con ρ = 1 − ωω0
, llamado factor de resonancia.
k
Si ω = ω 0 , la ecuación se reescribe y 00 + ω 20 y = Fm0 cos ω0 t. En Resonancia
este caso, el método de coeficientes indeterminados se modifica y
da una particular
yp =
F0
t sen ω 0 t,
2mω0
Las amplitudes máximas crecen con t por el factor t existente.
3
El caso c > 0 (amortiguado)
y = yh + yp
Vimos que yh → 0 para t → ∞. La solución y = yh + yp es la "transitoria". Después de un tiempo prevalece yp , que se llama la
"estacionaria" y que oscila con la frecuencia de la entrada.
4