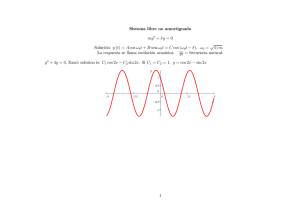
Sistema libre no amortiguado my// + ky φ 0 Solución: y (t) φ Acosω #t

.
Sistema libre no amortiguado
my 00 + ky = 0
Solución: y (t) = A cos ! 0 t + B sen ! 0 t = C cos (! 0 t
), ! 0 =
La respuesta se llama oscilación armónica. !2 0 = frecuencia natural.
y 00 + 4y = 0, Exact solution is: C1 cos 2x C2 sin 2x. Si C1 = C2 = 1; y = cos 2x
p
k=m:
sin 2x
y
1.0
0.5
-5
-4
-3
-2
-1
1
-0.5
-1.0
2
3
4
5
x
Sistema libre amortiguado
my 00 + cy 0 + ky = 0
Ecuación característica:
2
+
c
m
+
k
m
1.- c2 > 4mk sobreamortiguado
no oscilan
2.- c2 = 4mk amortiguamiento crítico
3.- c2 < 4mk subamortiguado
p
c
1
En 1.- y 2.-, poniendo
= 2m
y
= 2m
c2 4mk (Luego
Soluciones:
1.- y = c1 e (
= 0. Raíces:
< ), resulta
)t
+ c2 e
2.- y = (c1 + c2 t) e
En 3.- hemos puesto
= i!
con ! =
1.- Sobreamortiguado
3.- e
p
1
2m
t
c2 . Así,
1
=
(
1
=
1
2m
p
(
c2
);
4mk
2
=
( + ):
( + )t
t
(A cos ! t + B sen ! t) = Ce
4mk
c
2m
=
i! ) ;
t
cos (! t
2
=
)
( + i! )
2.- Amotiguamiento Crítico
Ejemplos con distintas condiciones iniciales
3.- Subamortiguado
Oscilaciones Forzadas
my 00 + cy 0 + ky = r (t)
La solución general se obtiene por superposición de la solución yh del sistema homogéneo (oscilaciones libres) con una solución
particular yp . Resulta particularmente importante el caso en que la entrada es una onda r (t) = F
p0 cos !t de frecuencia !=2 .
1
c
c2 4mk.
Recordemos que las soluciones de la ecuación característica son = 2m
2m
Caso amortiguado.
Si c > 0 no puede haber soluciones imaginarias puras de la EC., de modo que la aplicación del método de coe…cientes indeterminados
llevará a una solución de la forma yp = a cos (!t
) : La solución yh del homogéneo, por su parte, tiende a cero cuando t ! 1;
actuando sólo en el transitorio. En el estacionario el sistema oscilará con la frecuencia de entrada, con algún desfasaje :
Caso no amortiguado.
El sistema libre oscilaría con la frecuencia natural ! 0 . Si ! 6= ! 0 el método de coe…cientes indeterminados da una solución
particular
F0
cos !t:
yp =
m (! 20 ! 2 )
Esta solución, cuya amplitud máxima crece cuando !
armónica.
! 0 es chico, se superpone con la fundamental produciendo una oscilación no
y
y
4
4
3
3
2
2
1
1
x
1
2
3
4
5
6
7
8
x
9
1
−1
−1
−2
−2
−3
−3
−4
−4
cos 3t + 3 cos t
2
3
4
5
6
7
cos t + cos 2t
Si ! = ! 0 , la ecuación se reescribe como y 00 + ! 20 y =
cos ! 0 t. Ahora i! 0 es solución de la EC. y el método de
coe…cientes indeterminados obliga a proponer una solución del
tipo t (a cos ! 0 t + b sen ! 0 t) : Haciendo los cálculos se obtiene
F0
t sen ! 0 t, una oscilación cuya amplitud crece con t
yp = 2m!
0
F0
m
3
8
9